拉格朗日插值
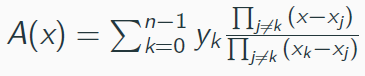
构造原理：当x=xk时A(xk)=yk;
快速傅里叶变换
复数与复平面
为了将数域扩大，引入虚数，详情请见数学选修2-2。
欧拉公式
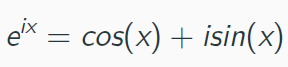这个公式在FFT中会用到。
多项式：n次多项式,->最高次为n-1，n个点可以确定唯一的n次多项式。
多项式求值：秦九韶算法，O(n)的时间求出多项式的一个点值表达。
多项式乘法：可以在n^2的时间内计算，这个比较简单，两个n次多项式可以乘出2n-1次多项式。
多项式加法：(x1,y1)(x1,y2)-> (x1,y1+y2)这个可以O(n)算。
如果我们已经知道了A和B的点值表达，我们可以在O(n)的时间算出C的点值表达。
圆周卷积：不会，留坑代填。
卷积定理：我们做两个多项式的卷积(乘法)复杂度是n^2，如果我们把多项式转成点值表达，再把点值表达加起来，在把点值表达用插值法转成多项式，如果这三个步骤的复杂度都没有超过n^2，那么我们可以算是优化成功了。
在一个xi上做点值运算的算法叫DFT(离散傅里叶变换)。
如果我们快速的完成所有xi的点值表达运算，时间复杂度为nlogn，这就是FFT(快速傅里叶变换)。
离散傅里叶变换
n次单位根：满足x^n=1的复数。
n次单位根恰好有n个，对于它们分别是e^2πki/n，k[0-n-1]。
理解一下就是把k个圆n等分。
k=1时的单位根为主n次单位根，记做wn，其他单位根可以看做wn的幂。
DFT的特殊点指的就是n次单位根。
一遍DFT可以求出A(wn0),A(wn1).....A(wnn-1)
设结果为F。
那么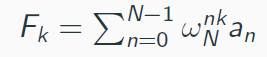
我们最终还是需要知道系数表达，所以还需要插值运算。
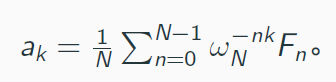
可以用矩阵去验证。
单位根的性质
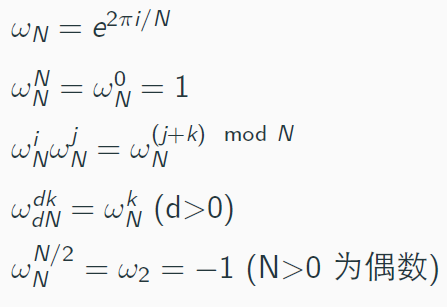
第一条和第二条是最基本的，第三条就是根据欧拉公式(可以脑补复平面)，第四条和第五条是折半引理。
这两条是消去引理。
现在我们有了一个长度为2的整数次幂的多项式。
然后我们可以把x的下标按照奇偶分组。
然后再按照上面的性质瞎搞一下。
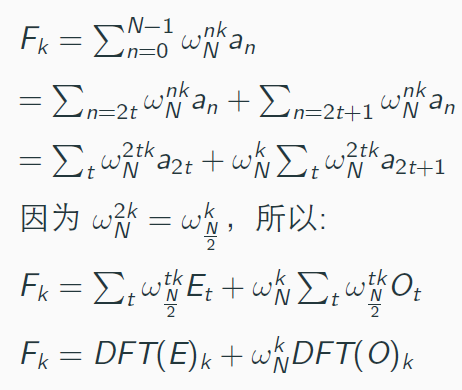
我们成功的把问题的规模减小了一半。
然后我们就可以按照上面的方法一直分治下去。
注意我们是吧长度为l的区间分成两半，一半为wk，一半为wk+2/n=-wk，所以算的时候加减注意一下。
蝴蝶操作
我们发现最后找出来的序列的下标和原来下标有一些神奇的联系。
于是我们可以O(n)算每个数的二进制翻转，然后可以迭代做了。
快速数论变换(NTT)
复数运算常数太大，如果我们找到一个数论上的东西来代替wn，那么我们可以完成在模意义下的FFT了。
阶与原根
x的阶x^k=1(%p)。
p的原根：满足x的阶=p-1的最小的x，即为g。
g^(p-1)/n可以代替wn。
多项式全家桶
多项式求逆
利用倍增搞。
首先这个科技只能用于模意义下的，没有模的是一个无解的问题。
然后我们令B为在模2^(n-1)下的逆，B‘为模2^n下的逆。
(B-B')=0(%2^(n-1))
(B-B')^2=0(%2^n)
B^2-2*B*B'+B'^2=0(%2^n)
AB^2-2*B+B'=0(%2^n)
B'=2*B-2*A*B^2(%2^n)
然后就倍增做
多项式ln
也就是我们要求一个G函数
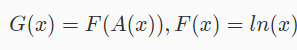
对两边求导，根据复合函数的求导方法，还有ln的导为1/x。
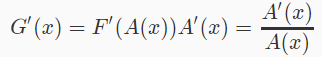
然后就求个导求个逆就可以算出G‘
然后再用求导的逆过程给它还原回去，好像叫什么不定积分。
多项式exp
这个东西还得用到什么牛顿迭代之类的高端玩意，直接放个结论吧。
多项式开根
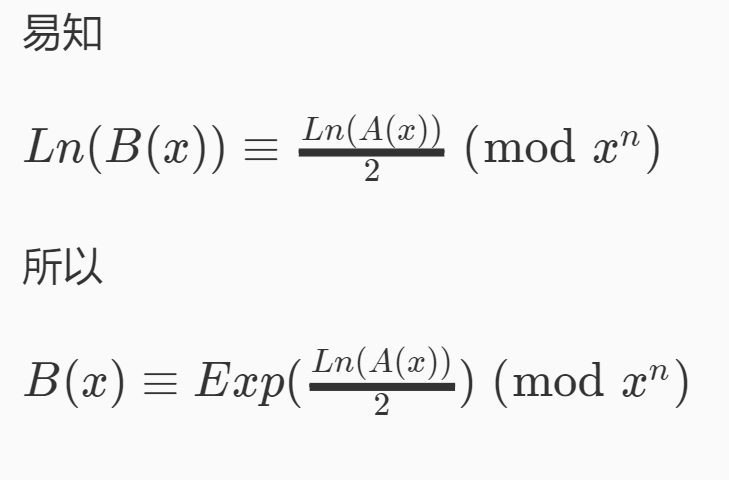
多项式除法 咕咕咕
多项式多点求值 咕咕咕
多项式快速插值 咕咕咕