接触第一个非线性的逻辑结构,也就是树形结构。

那么树形结构我们会学习哪些主要的知识点呢?我们会学习两种树形结构,分别是二叉树和树和森林。在二叉树当中我们将学习二叉树的基本概念,也就是它的定义、特点以及对应的存储结构。然后我们将学习二叉树的遍历,以及一种特殊的二叉树叫做线索二叉树。最后我们将介绍几个有关二叉树的应用,分别是二叉排序树、平衡二叉树以及哈夫曼树。而在树和森林当中我们会学习树的基本概念,存储结构以及它们的遍历方法。还有一个重要的考点就是树、森林、二叉树之间的相互转化方法。最后我们将介绍树的一个小应用叫做并查集。好,这就是本章所要学习的主要知识点。

那么在本节课当中我们会先讲树的基本概念。
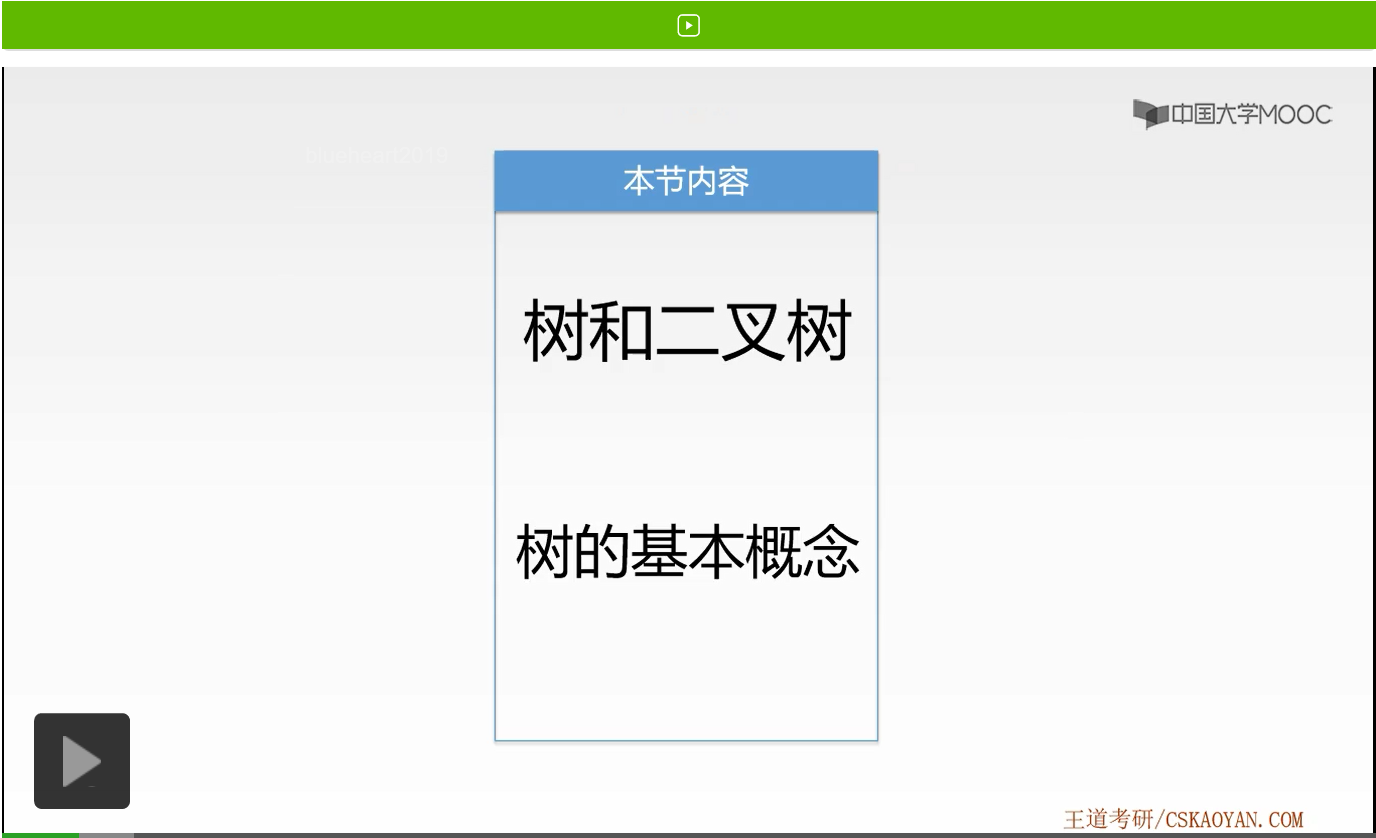
在第一章当中我们学习过一种树形结构,它是一对多的关系。所以首先树,一定是一种逻辑结构。树是n个结点的有限集合,这里n是大于等于0的。所以树是可以为空的。当n=0时称为空树。那么n不等于0时也就是任意非空树应该满足哪些条件呢?第一个条件是有且仅有一个特定的称为根的结点。
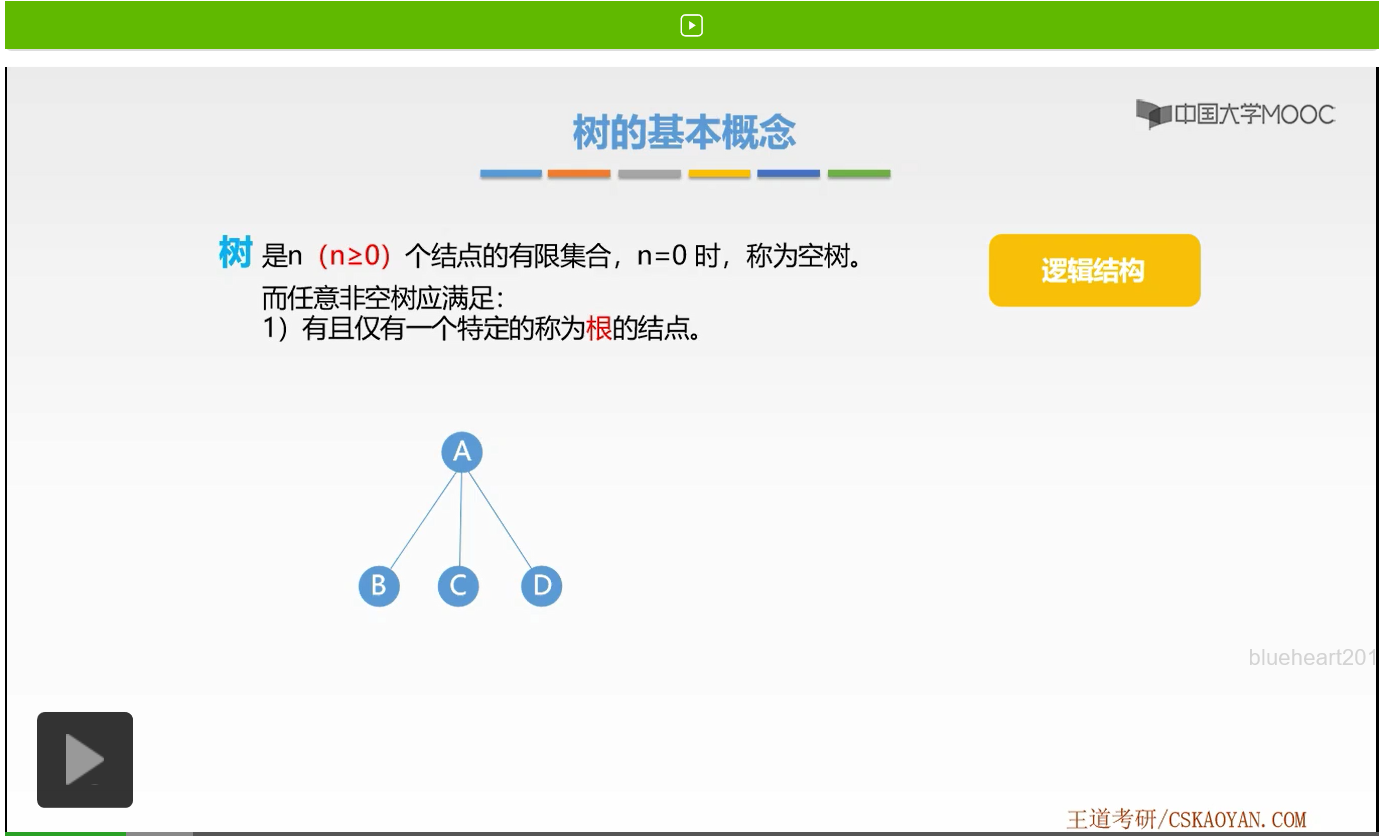
那么在这样一棵树当中,它的根是不是就是A结点啊。根结点这个称呼非常形象,也就是代表着最源头的那个意思。
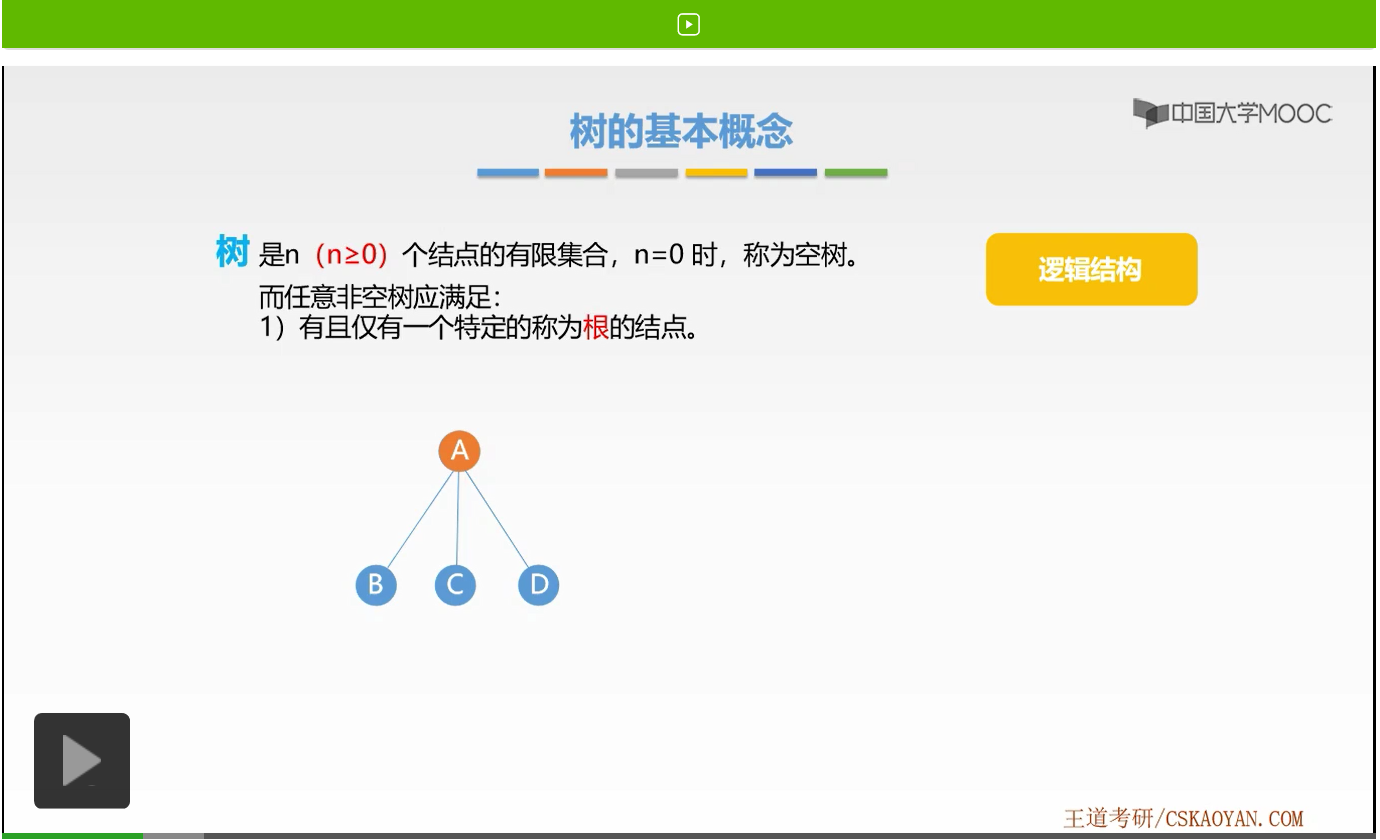
接着我们来看第二个需要满足的条件就是当n大于1时,也就是一棵非空树时,其余结点可分为m个互不相交的有限集合。其中每一个集合本身又是一棵树,称为根结点的子树。我们可以把B、C、D三个结点看作以A为根,树的子树。B、C、D三个结点,分别代表着只有1个结点的子树,当然它也可以有多个结点。
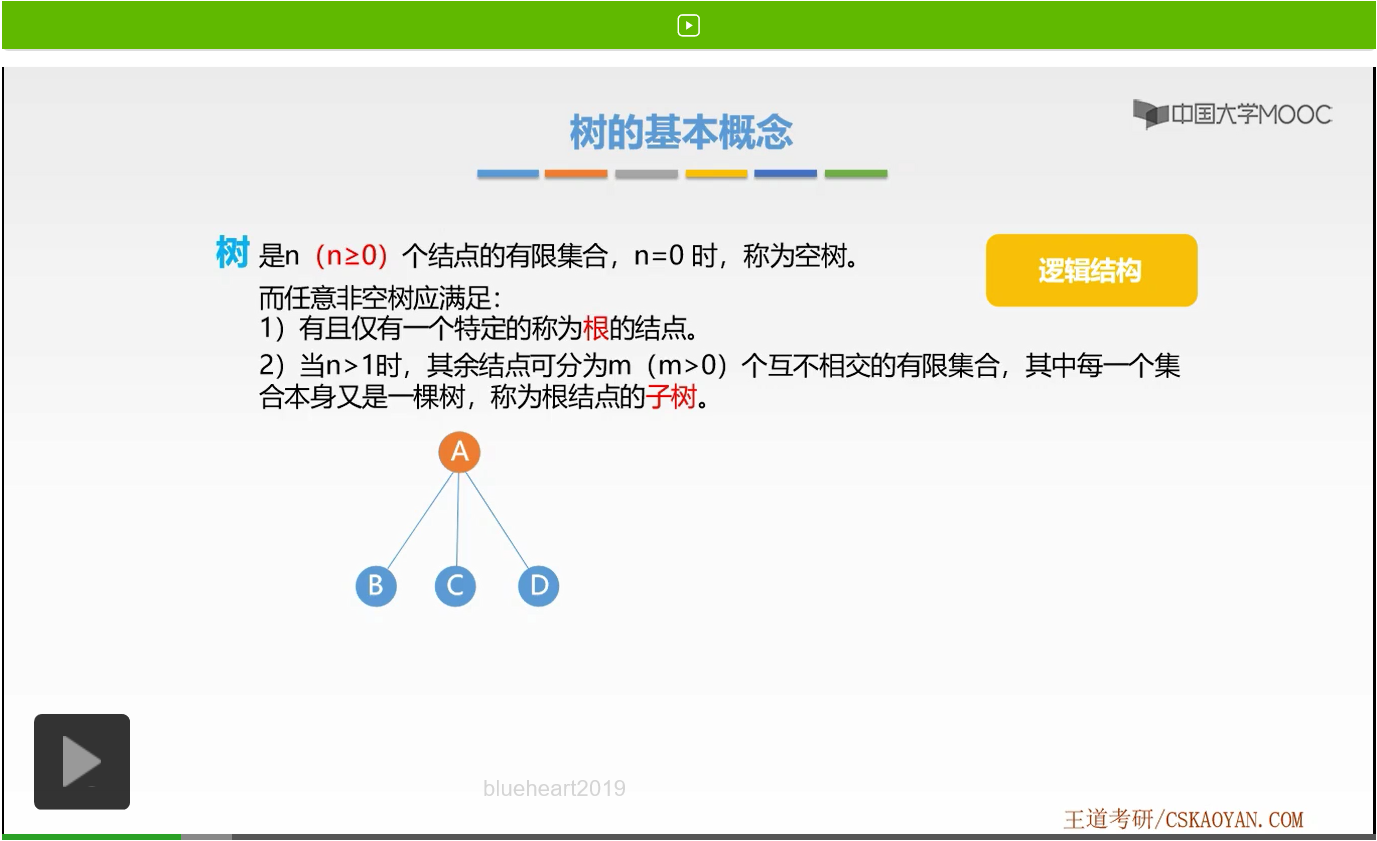
比如我们再增加两个结点,那么B、E、F就组成了这样一棵子树。在这棵子树当中,B是子树的根。好,这就是第二个所满足的条件。那么说到这里大家有没有想到,第三章我们学过一种叫做递归定义的知识点,大家有没有发现树的定义是不是就是一种递归的方法啊,树是一种递归的数据结构。那么大家回忆一下,树作为这样一种树状结构的逻辑结构,它有哪些特点呢?第一个特点是除根结点以外,每一个结点都有唯一的前驱结点。例如在PPT当中的这棵树,B、C、D三个结点的前趋结点是A。E、F的前趋结点是B,它们都有唯一的前趋结点。而每一个结点都有0个或多个后继结点,A的后继结点是B、C、D三个,B的后继结点是E、F。而E、F、C、D的后继结点是0个。好,这就是前趋结点以及后继结点的知识。
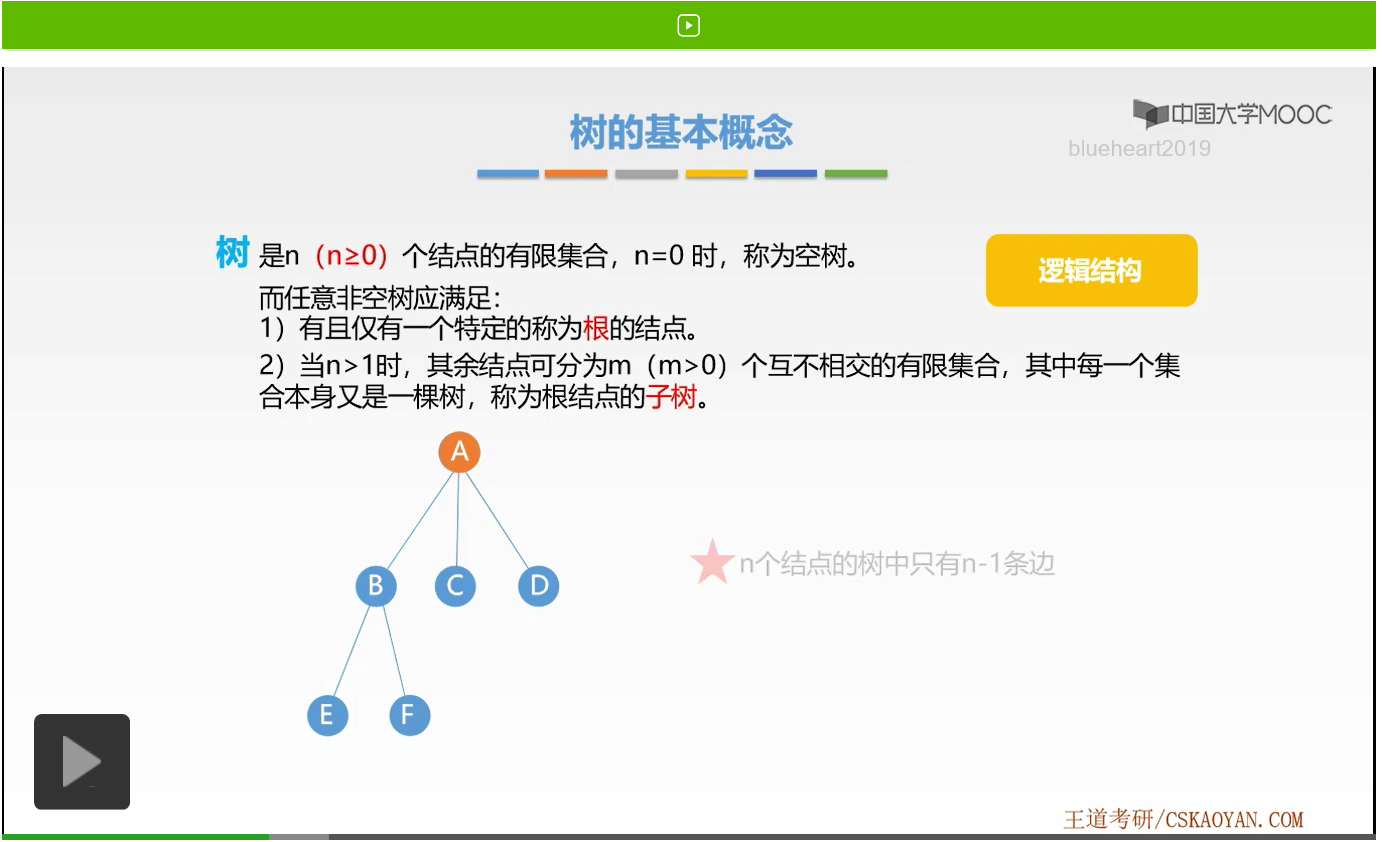
那么我们有这样一个结论,n个结点的树中,只有n-1条边。它是怎么样得来的呢?正如我们刚才所说,每一个结点都有唯一的前趋结点,但是除了根结点以外。那么边是不是代表着这样一种前趋后继的逻辑关系啊,而A是没有前趋结点的,所以有n-1条边。这就是我们为什么有这样一条结论。好,这就是树的定义。

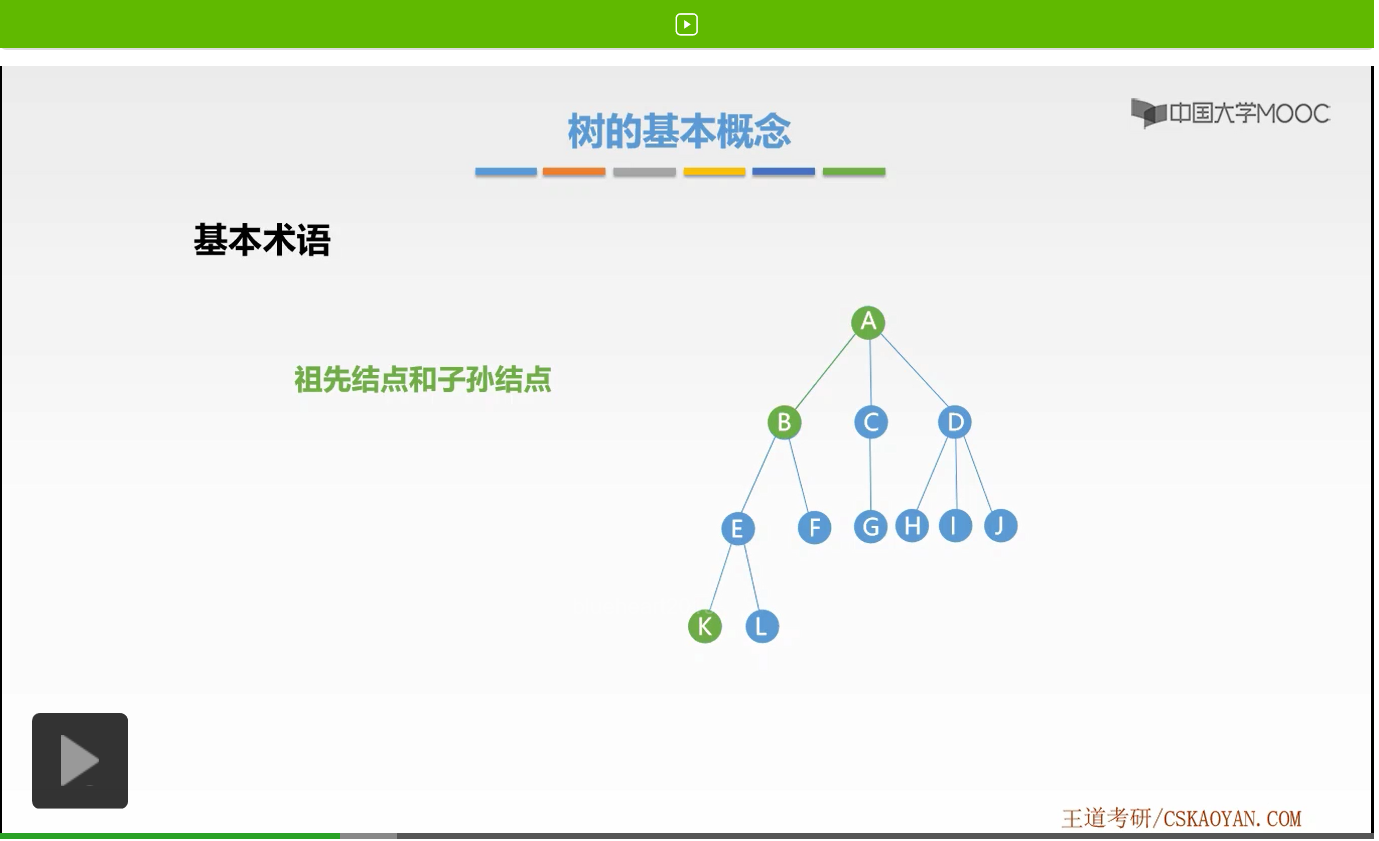
接下来我们来学习几个重要的树的基本术语。我先给大家画出一个树的例子,方便我们理解基本术语。首先第一对基本术语是祖先结点和子孙结点,它们代表什么样的结点呢?我们来看这样一个例子。
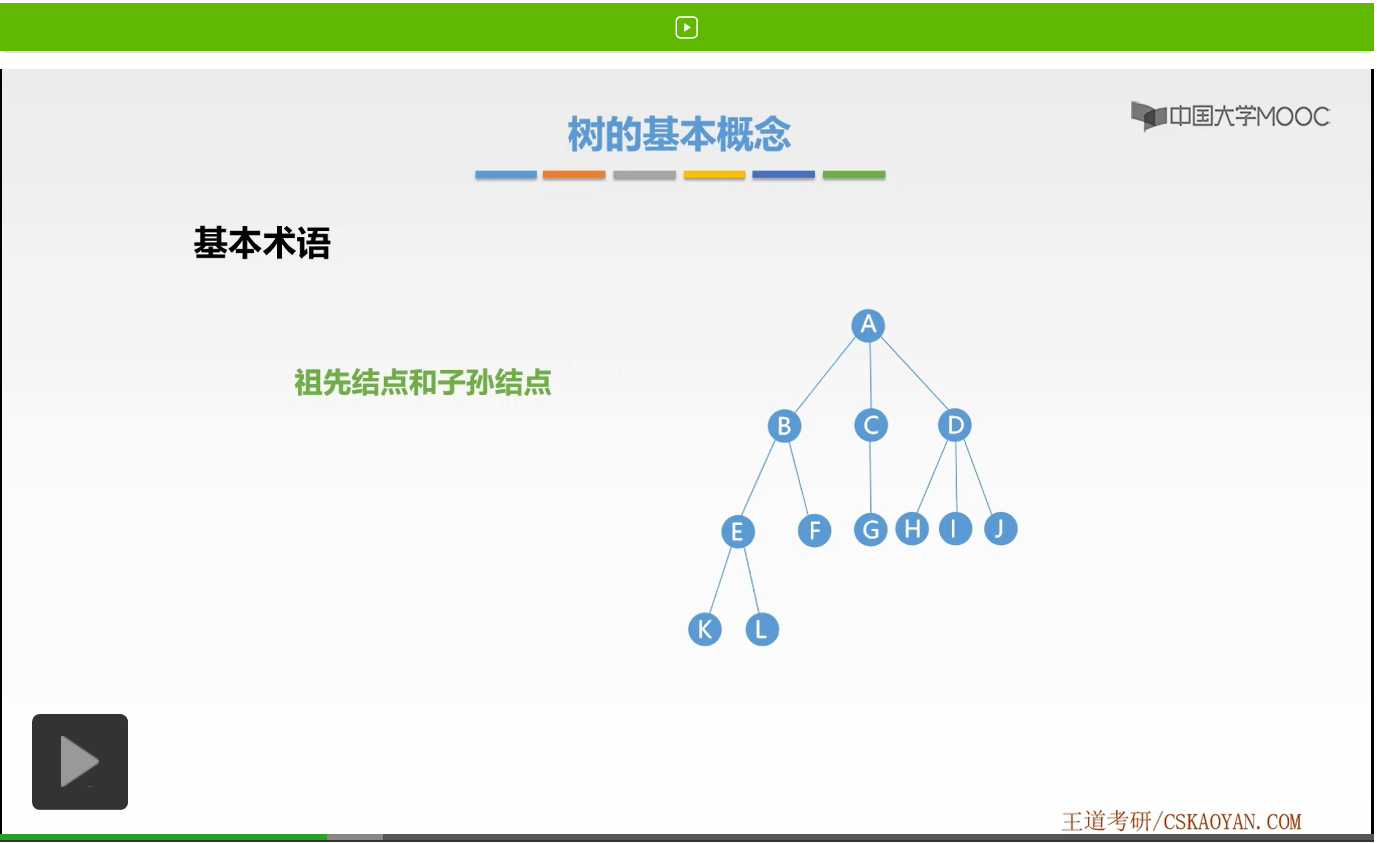
现在我们标记K,若以A,也就是以根结点出发,怎样寻找到K这样一个结点呢?
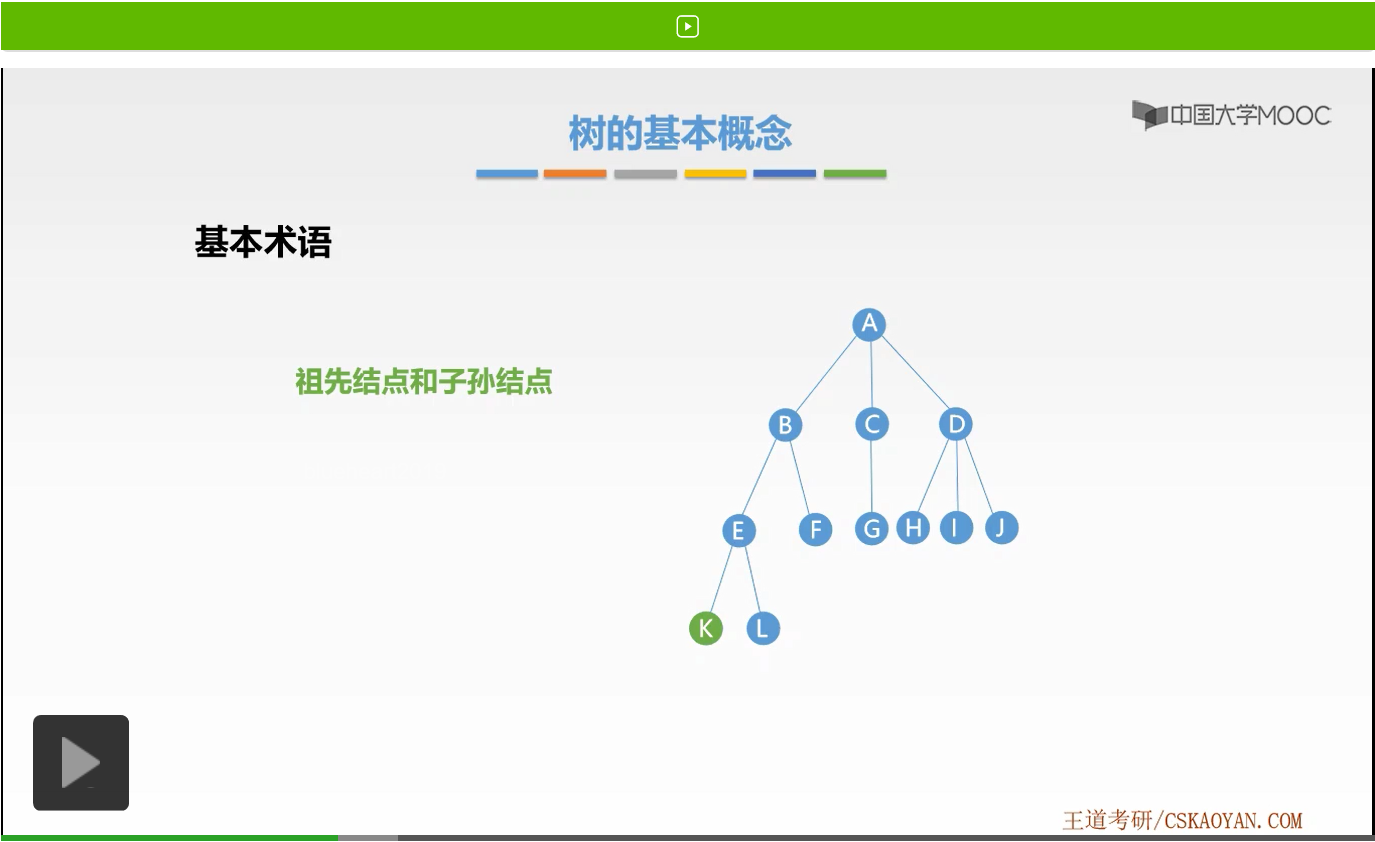
我们会按照这样一个路径,这样一个顺序来找到K结点。那么在该路径上除了K结点以外,所有的结点都可以称为K的祖先结点。而反过来,K则是它们的子孙结点。这就是祖先结点和子孙结点的概念。
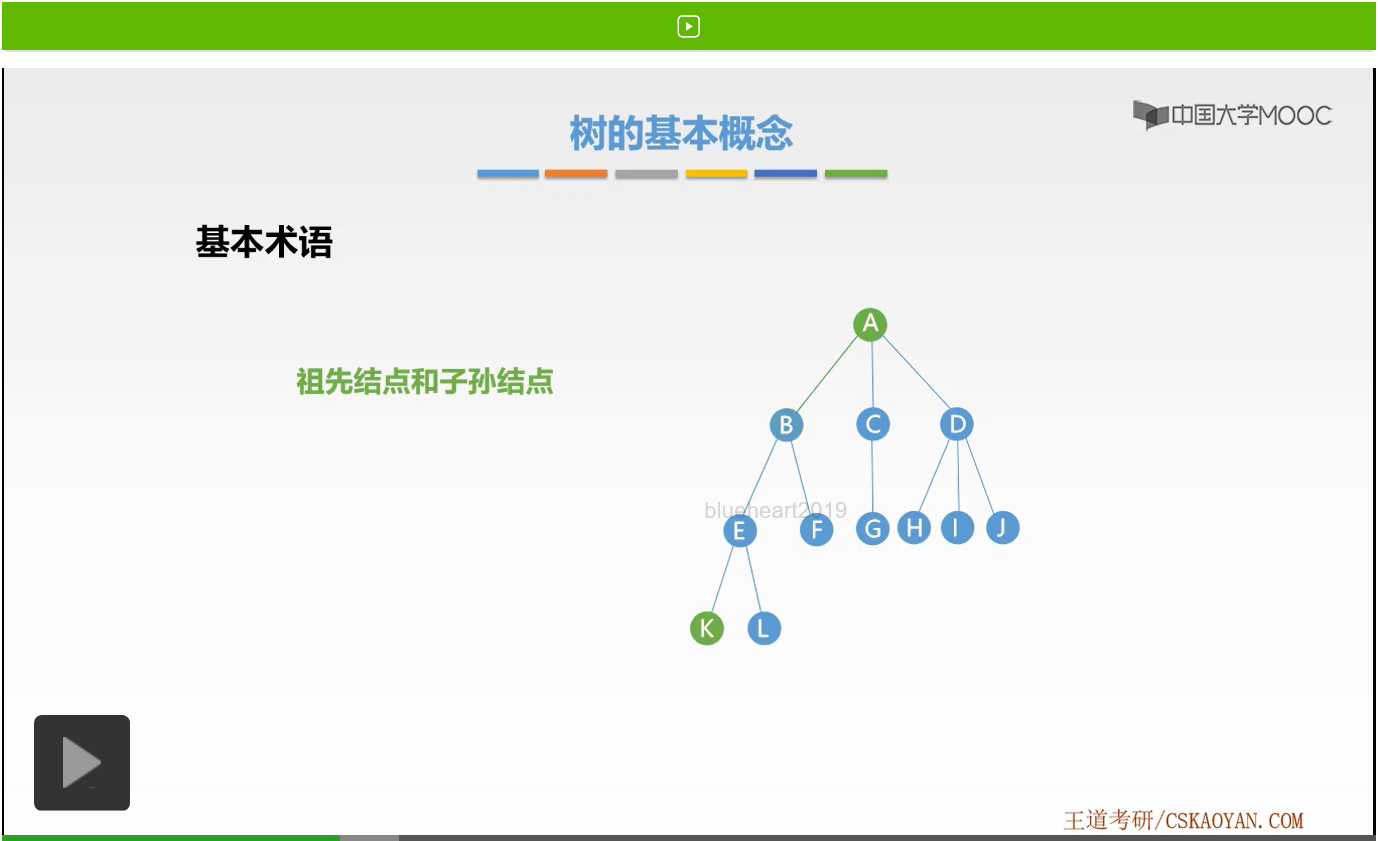
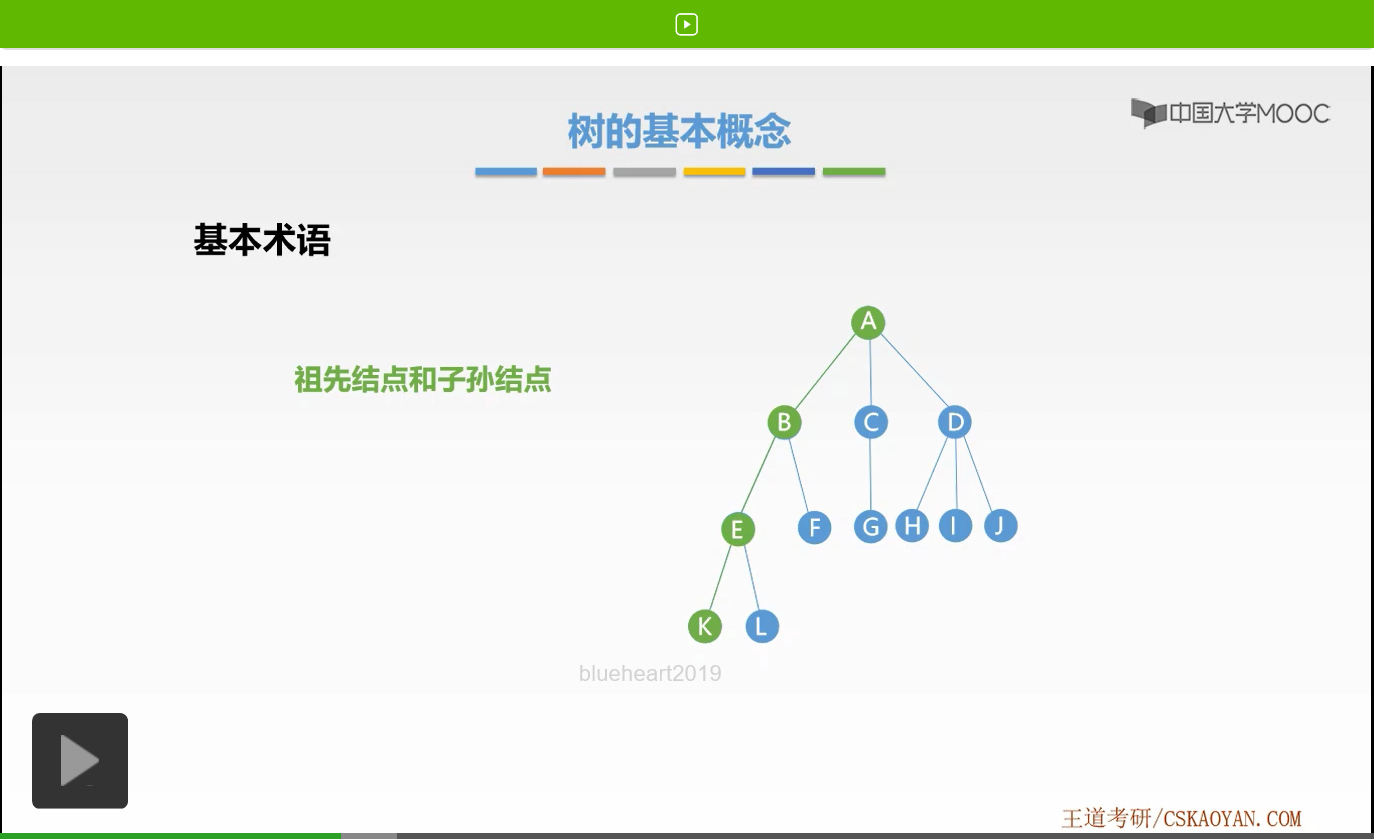
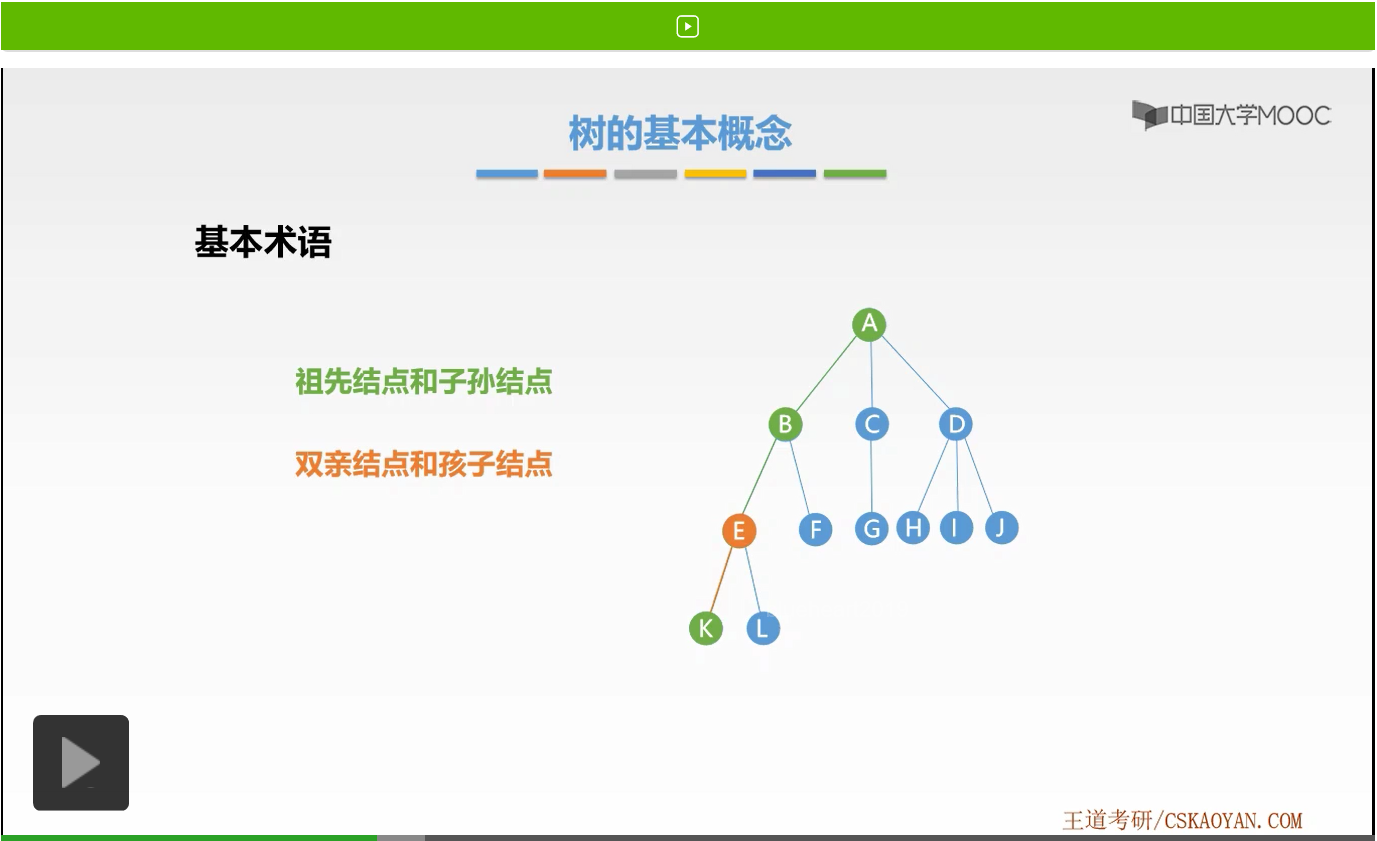
好,接下来我们来看第二对结点,就是双亲结点和孩子结点。什么叫双亲结点,什么又叫做孩子结点呢?还是来举一个例子,大家就明白了。那么我们发现在该条路径上,离K结点最近的祖先结点是E结点。也就是说,E是K的前趋结点。那么此时,我们就把E称为K的双亲结点,而K称为E的孩子结点。这就是双亲结点以及孩子结点的概念。

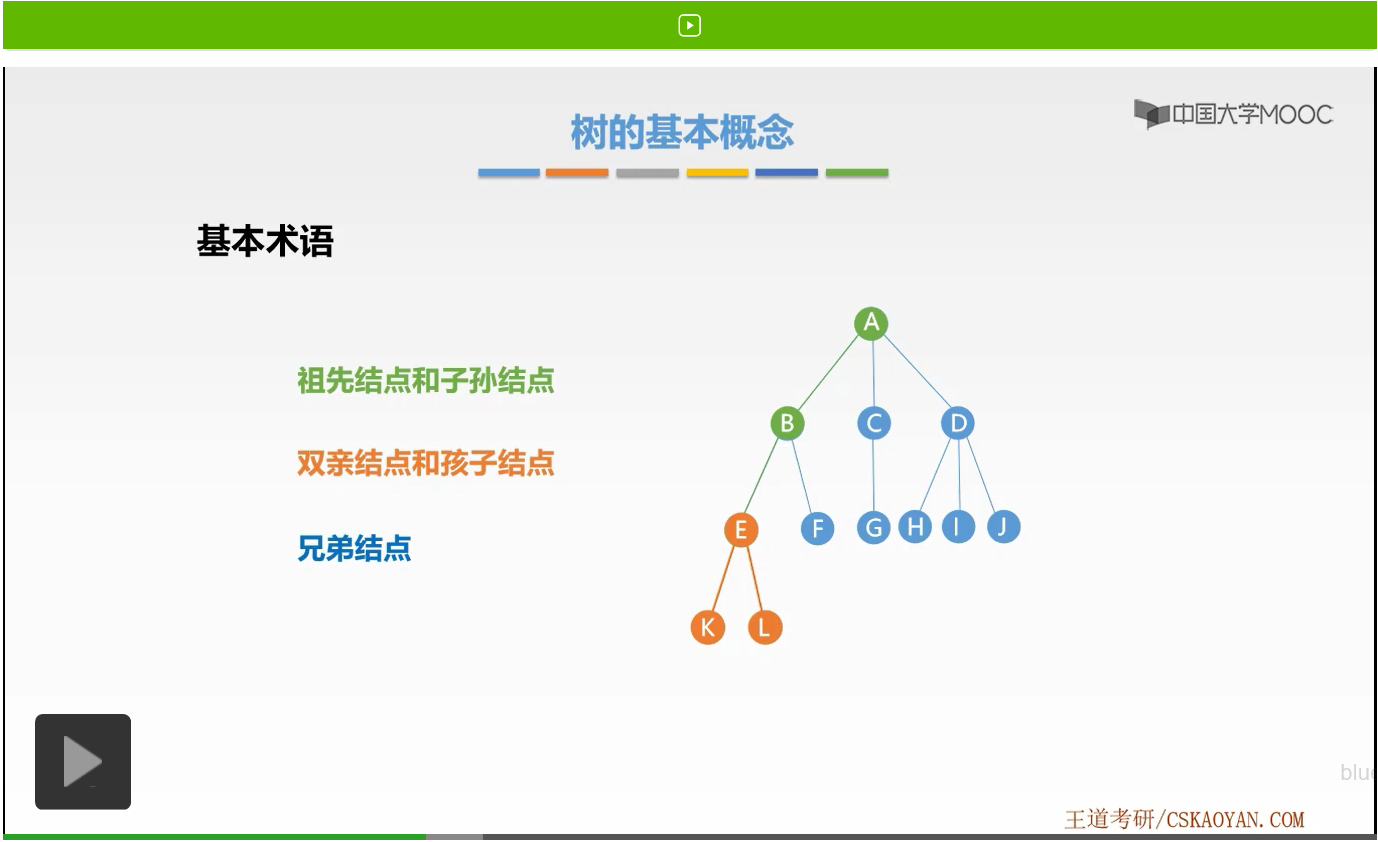
最后我们还有一个结点叫做兄弟结点。什么是兄弟结点呢?我们发现既然E是作为双亲结点,是不是还有L结点啊。

所以此时我们把L、K称作为兄弟结点,它们有共同的双亲结点。好,这就是五种结点的概念。

接着我们来学习第二个基本术语,也就是度的概念。什么是度呢?树中一个结点的子结点的个数称为该结点的度。大家注意一下这里是子结点。和我们之后学习图的度有细微的差别。
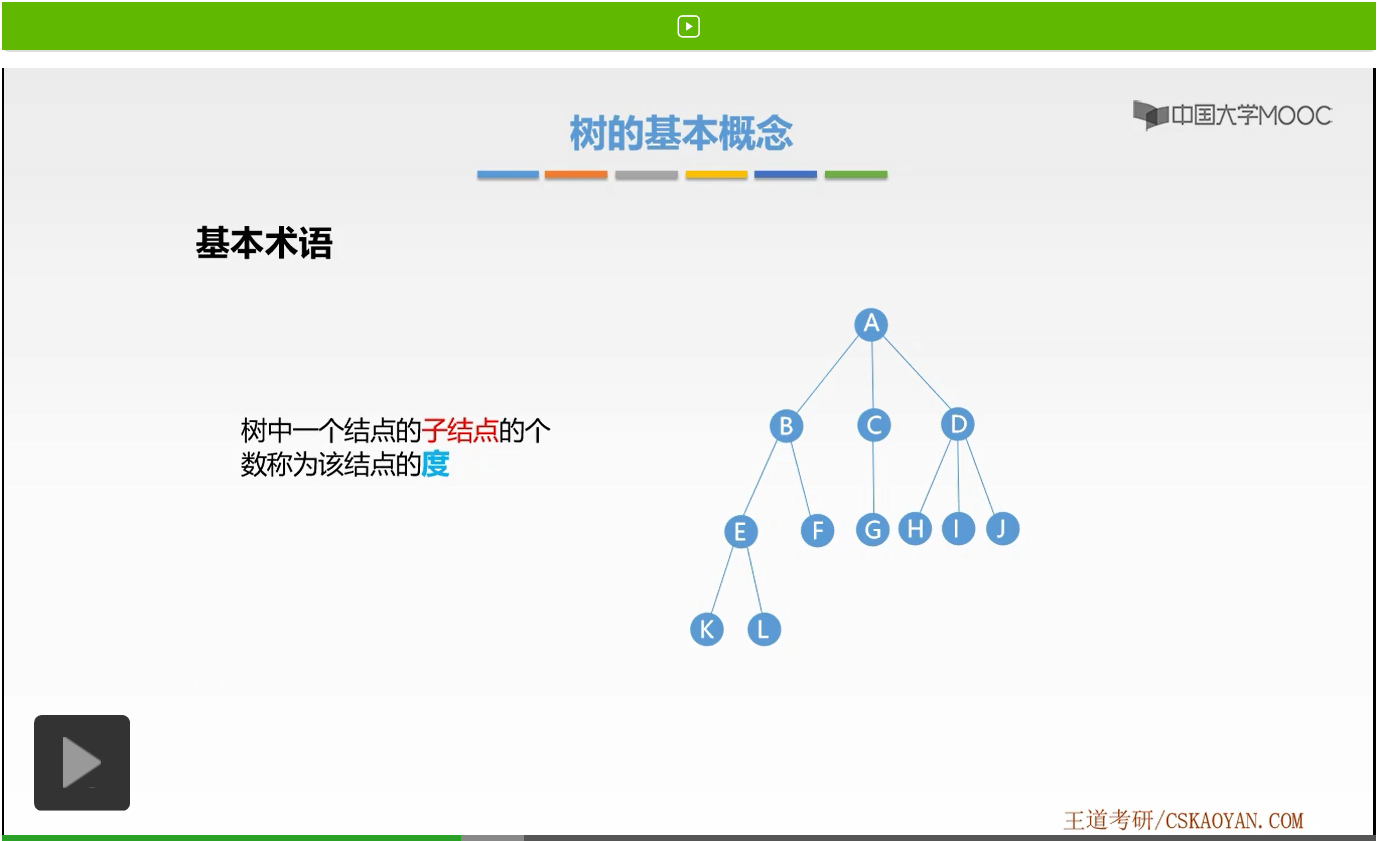
接下来我们就来举个例子。我们标记B结点,它的度是多少呢?
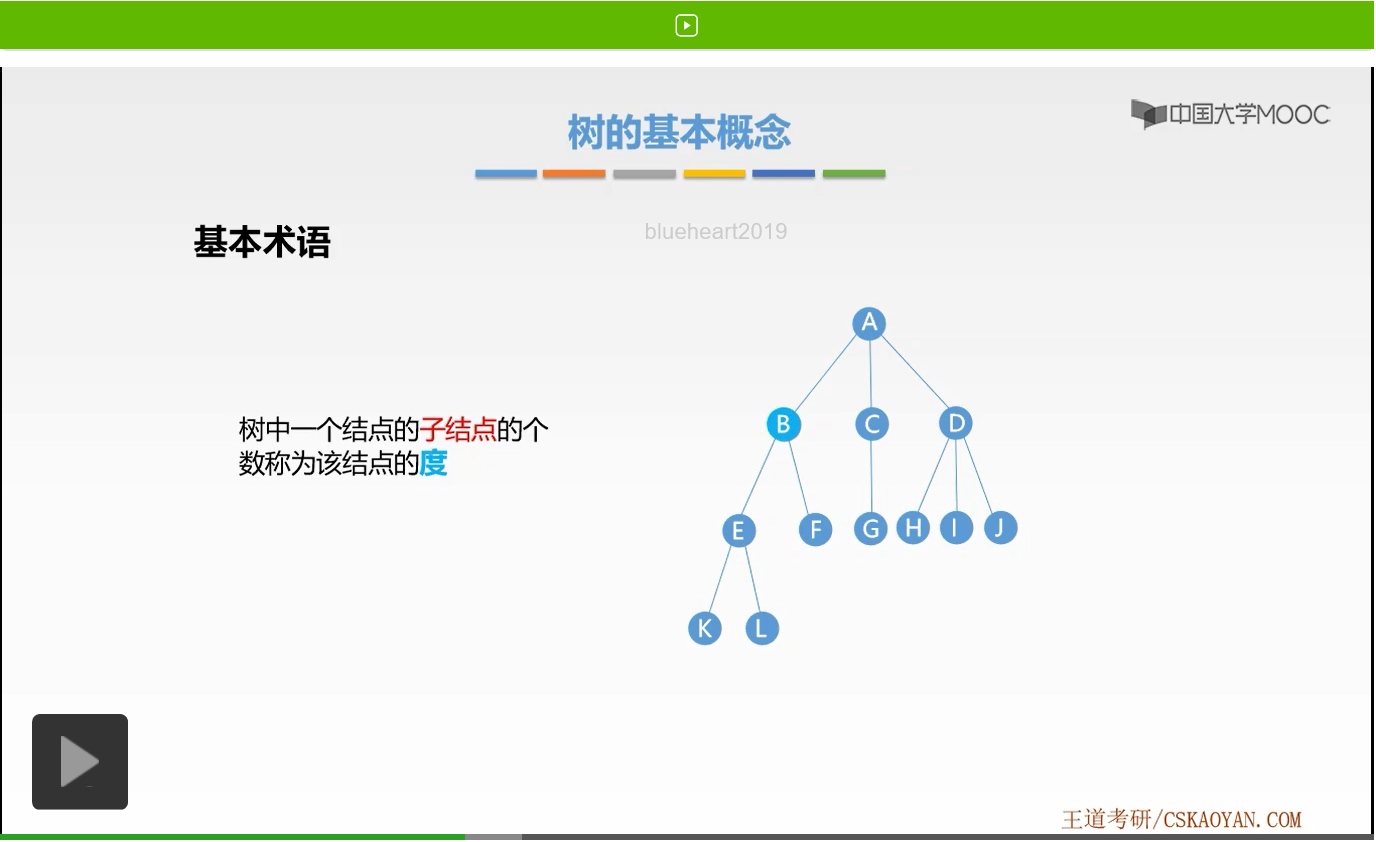
它有两个子结点,分别是E和F,所以B结点的度为2。好这是结点的度。

那么树的度是什么呢?我们称树中最大度数称为树的度。在这棵树当中,A结点度为3,B结点的度为2,C结点度为1,D结点度为3,E的度为2,其余的结点度都为0。所以,树的度为3,是所有结点度的最大值。好,这就是度的相关概念。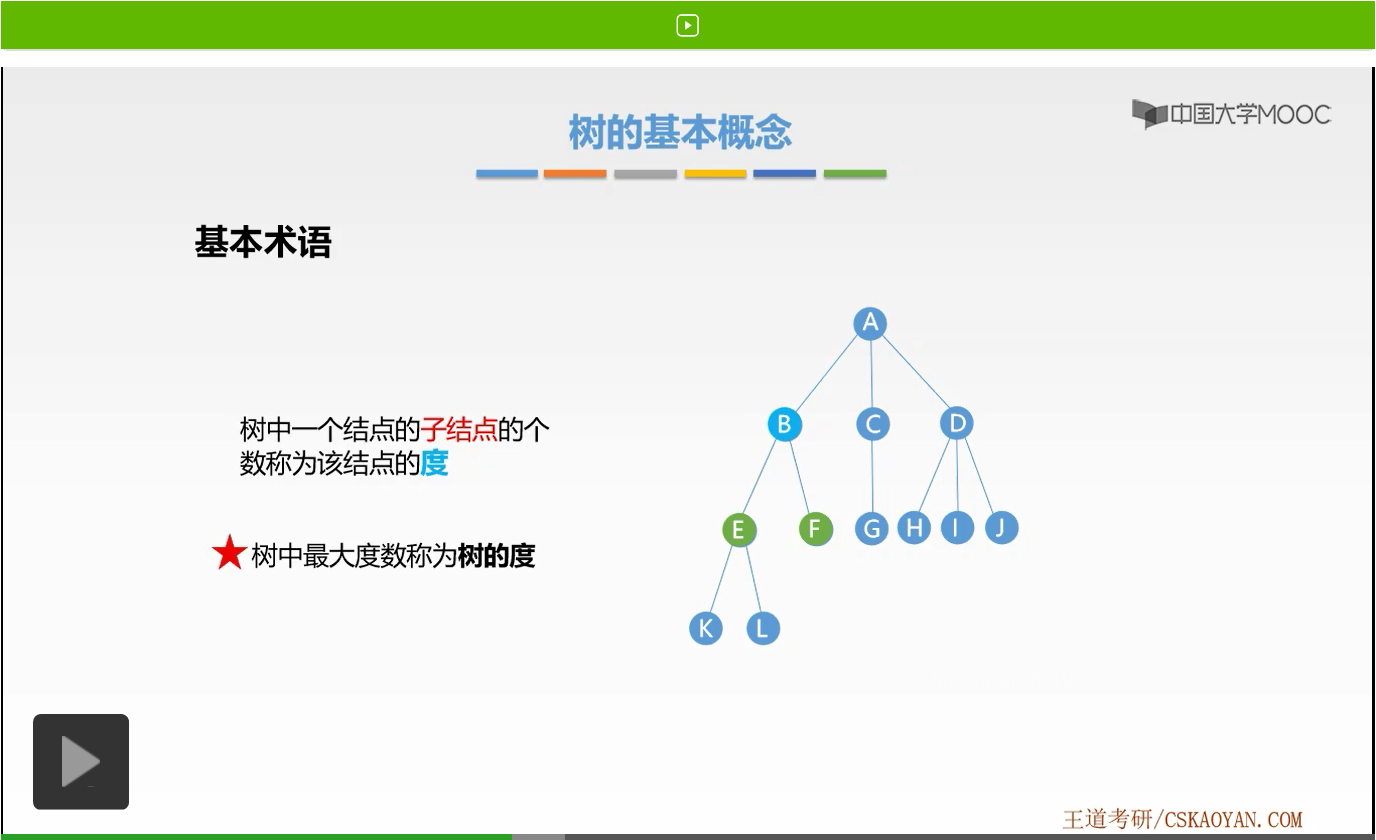
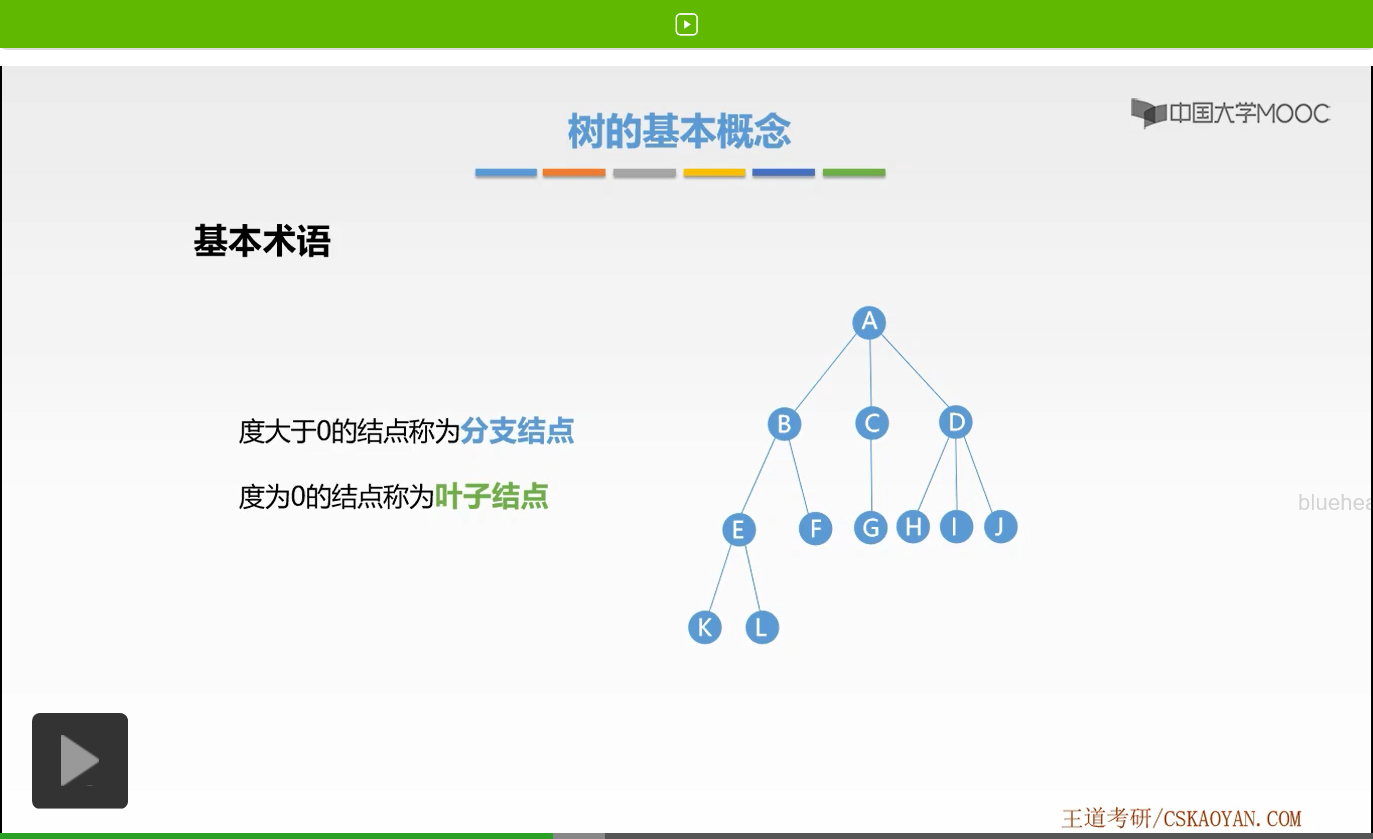
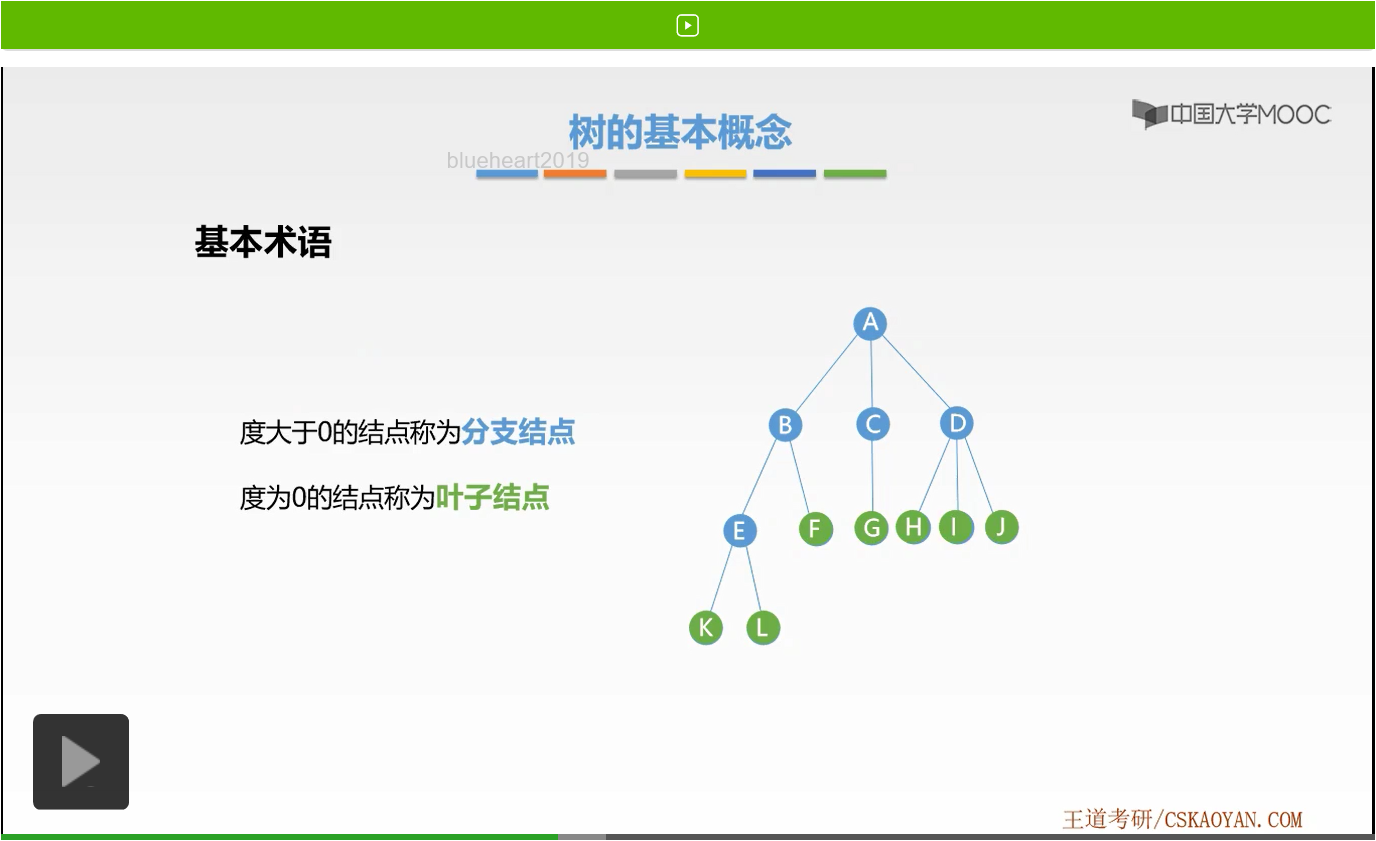
接着我们来学习下一段基本概念,也就是分支结点和叶子结点。什么是分支结点呢?度大于0的结点称为分支结点,也就是说它有孩子结点,那么在这个过程当中A、B、C、D、E就是分支结点,它们都有孩子结点,度都大于0。而其余的结点称为叶子结点,也就是度为0的结点,没有孩子的结点。好,这就是分支结点和叶子结点的概念。
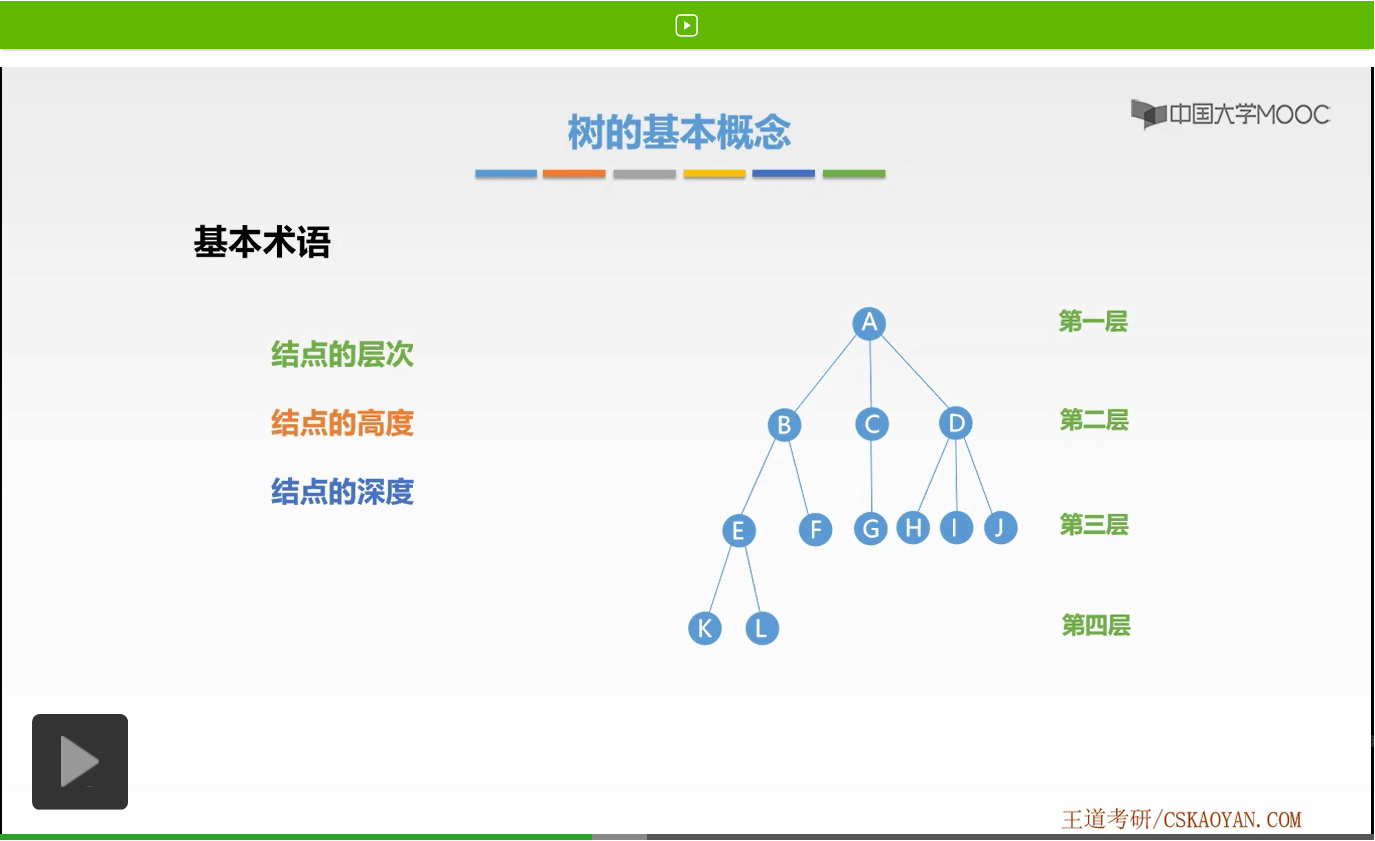
好,接下来是三个基本概念,分别是结点的层次、结点高度以及结点的深度。什么是结点的层次呢?我们将根结点也就是A结点定义为第一层,接下来也就是第二层、第三层以及第四层。大家要注意一点的是,有些教材可能也称第一层为第0层,在做题时我们也需要注意一下。好,接下来是结点高度。什么是结点的高度呢?它是从叶结点开始自底向上逐层累加的。
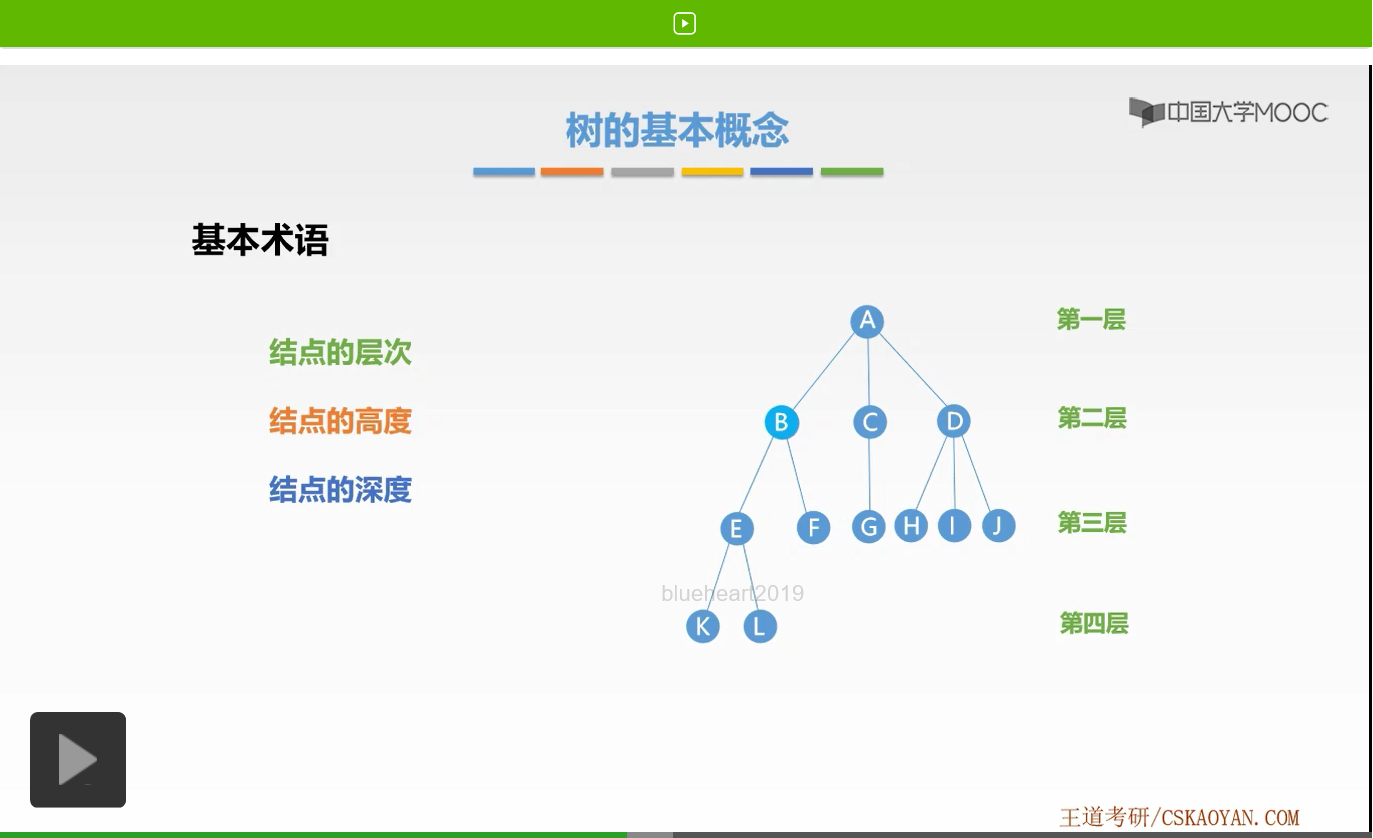
例如B结点高度为3,它分别经历了第四层、第三层和第二层。而结点深度刚好相反,它是从根结点开始自顶向下逐层累加的,所以B的结点的深度是2。从根结点开始,第一层、第二层。好,这就是结点的层次、高度以及深度的概念。
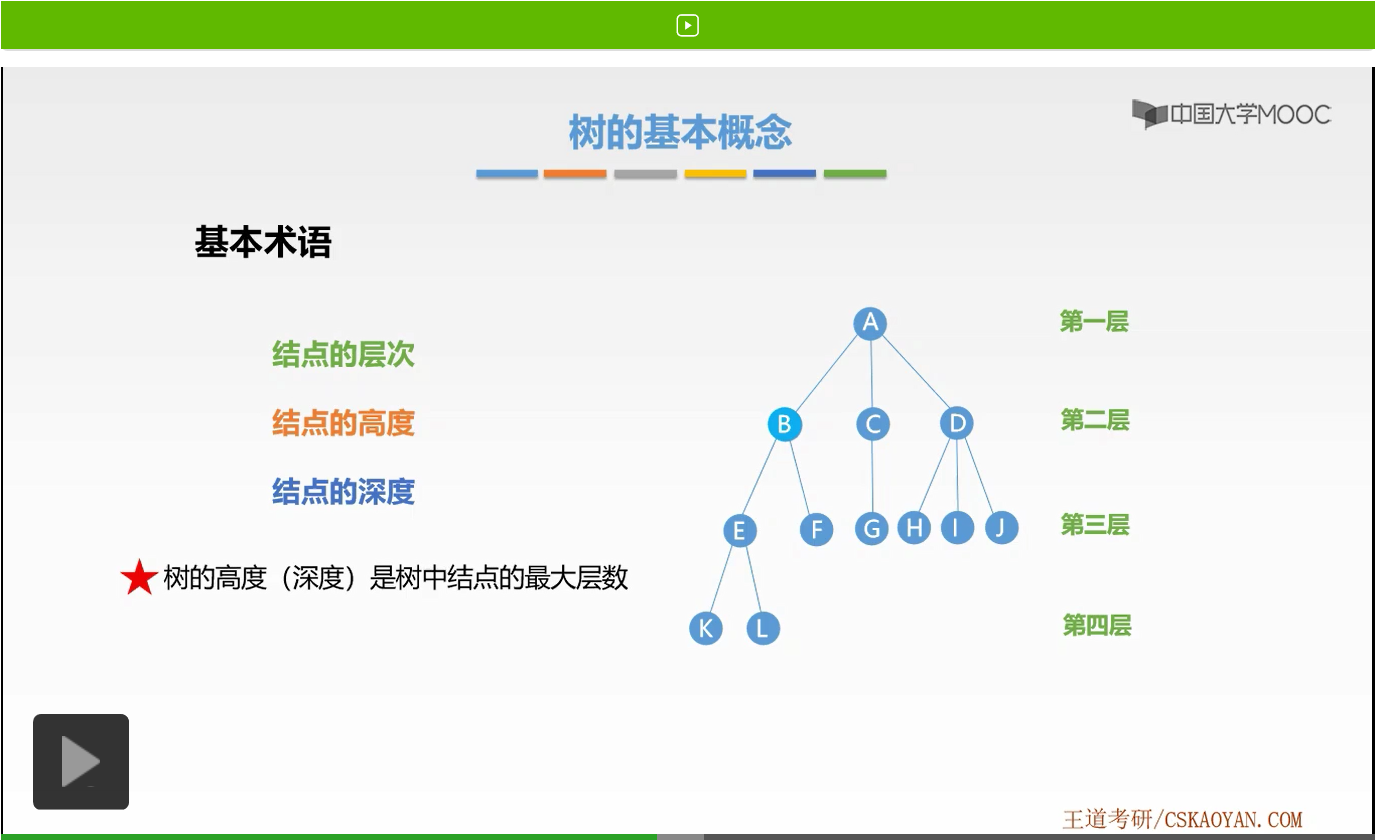
好接着我们还有这样的概念,树的高度或者是深度是树中结点最大的层数。为什么这里既是高度也是深度呢?有没有发现高度和深度是相等的。例如在这个例子当中,树的最大高度为4,最大深度也为4。这就是树的高度和深度。
好,接下来是有序树和无序树。