题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1213
问题描述
今天是依纳爵(Ignatius)的生日。他邀请了很多朋友。现在是晚饭时间。伊格内修斯想知道他至少需要多少张桌子。您必须注意,并不是所有的朋友都彼此认识,并且所有的朋友都不想和陌生人呆在一起。
解决此问题的一条重要规则是,如果我告诉您A认识B,而B认识C,则意味着A,B,C彼此认识,因此它们可以呆在一张桌子上。
例如:如果我告诉你A知道B,B知道C,D知道E,那么A,B,C可以留在一个表中,而D,E必须留在另一个表中。因此,伊格纳修斯至少需要2张桌子。
输入值
输入以整数T(1 <= T <= 25)开头,该整数表示测试用例的数量。然后是T测试用例。每个测试用例均以两个整数N和M(1 <= N,M <= 1000)开头。N表示朋友的数量,朋友从1到N标记。然后跟随M行。每行包含两个整数A和B(A!= B),这意味着朋友A和朋友B彼此认识。两种情况之间将有一个空白行。
输出量
对于每个测试用例,只需输出Ignatius至少需要多少个表。请勿打印任何空白。
样本输入
2
5 3
1 2
2 3
4 5
5 1
2 5
样本输出
2
4
并查集操作步骤:
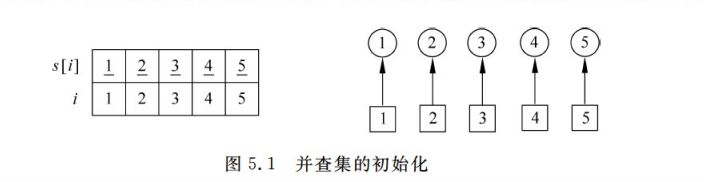
(1)初始化,定义数组int a[]以结点i为元素的并查集,一开始没有进行处理,每一个点都是孤立的集合,元素i的值表示它的集a[i],比如元素a[1]=1;
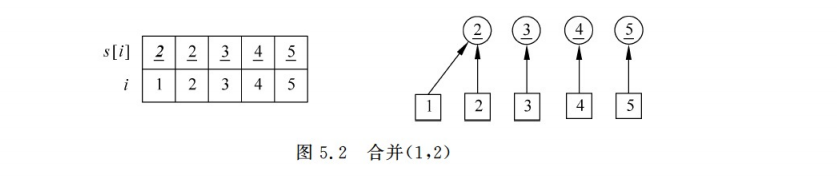
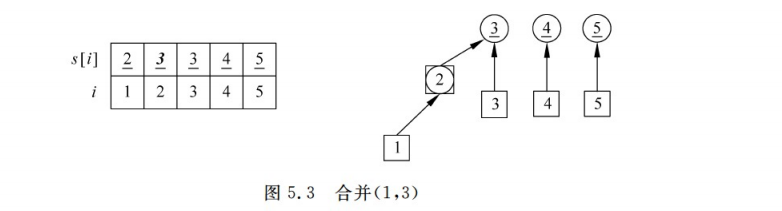
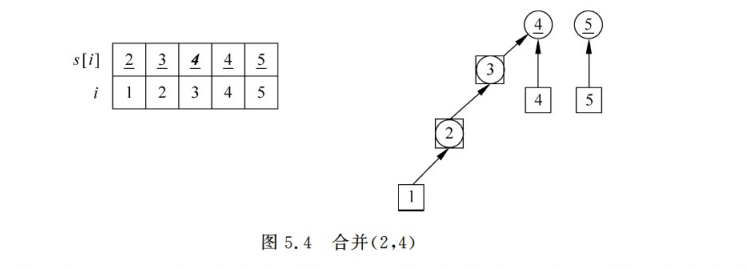
(2)合并,把有关系的合并在一起,比如本题目的例子(1 ,2),(2, 3),(4, 5)。如何理解呢,博主认为1,2,3有关系,那么先把1归入2,再把2归入3里面;这样的话1,2,3就属于3这个集合,依次下去,构成搜索树。
(3)查找,查找是一个递归的过程,直到找到一个元素和它的集相等为止,此时就找到了根节点的集
(4)统计有多少集合
1 /* 2 * @Descripttion: 3 * @version: 4 * @Author: ZKYAAA 5 * @Date: 2020-04-17 14:04:47 6 * @LastEditors: 请叫我ZK谕啊啊啊 7 * @LastEditTime: 2020-04-17 19:41:16 8 */ 9 10 #include <bits/stdc++.h> 11 using namespace std; 12 #define _for(i,a,b) for(int i=(a);i<=(b);i++) 13 const int MAXN=1050; 14 int a[MAXN]; 15 int height[MAXN]; 16 int i; 17 18 void init_set(){ //初始化 19 _for(i,1,MAXN){ 20 a[i]=i; 21 height[i]=0; //搜索树的高度 22 } 23 } 24 25 /* 26 int find_set(int n){ //查找递归实现 27 if(n!=a[n]) 28 a[n]=find_set(a[n]); //路径压缩 29 return a[n]; 30 } 31 */ 32 33 int find_set(int n){ //查找非递归实现 34 int r=n; 35 while(a[r]!=r) r=a[r]; //找到根节点 36 int i=n,temp; 37 while(i!=r){ 38 temp=a[i]; //用零时变量temp记录 39 a[i]=r; //把路径上元素的集改为根结点 40 i=temp; 41 } 42 return r; 43 } 44 45 void union_set(int x,int y){ //合并 46 x=find_set(x); 47 y=find_set(y); 48 if(height[x]==height[y]){ 49 height[x]=height[x]+1; //合并,树的高度加一 50 a[y]=x; 51 } 52 else{ 53 if(height[x]<height[y]) //把矮树合并到高树上,树高高度保持不变 54 a[x]=y; 55 else 56 a[y]=x; 57 } 58 } 59 60 int main(){ 61 int t,n,m,x,y; 62 cin>>t; 63 while(t--){ 64 cin>>n>>m; 65 init_set(); 66 _for(i,1,m){ 67 cin>>x>>y; 68 union_set(x,y); 69 } 70 int sum=0; 71 _for(i,1,n){ 72 if(a[i]==i) 73 sum++; 74 } 75 cout<<sum<<endl; 76 } 77 return 0; 78 }