求两条线段的交点

　　两条线段的两个端点坐标(x1,y1) (x2,y2) (x3,y3) (x4,y4)

　　b1=(y2-y1)*x1+(x1-x2)*y1

　　b2=(y4-y3)*x3+(x3-x4)*y3

　　D=(x2-x1)(y4-y3)-(x4-x3)(y2-y1)

　　D1=b2*(x2-x1)-b1*(x4-x3)

　　D2=b2*(y2-y1)-b1*(y4-y3)

　　交点(x0,y0)

　　x0=D1/D   y0=D2/D

推导：http://www.cnblogs.com/dwdxdy/p/3230485.html

E. Covered Points

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given nn segments on a Cartesian plane. Each segment's endpoints have integer coordinates. Segments can intersect with each other. No two segments lie on the same line.

Count the number of distinct points with integer coordinates, which are covered by at least one segment.

Input

The first line contains a single integer nn (1≤n≤10001≤n≤1000) — the number of segments.

Each of the next nn lines contains four integers Axi,Ayi,Bxi,ByiAxi,Ayi,Bxi,Byi (−106≤Axi,Ayi,Bxi,Byi≤106−106≤Axi,Ayi,Bxi,Byi≤106) — the coordinates of the endpoints AA, BB (A≠BA≠B) of the ii-th segment.

It is guaranteed that no two segments lie on the same line.

Output

Print a single integer — the number of distinct points with integer coordinates, which are covered by at least one segment.

Examples

input

9
0 0 4 4
-1 5 4 0
4 0 4 4
5 2 11 2
6 1 6 7
5 6 11 6
10 1 10 7
7 0 9 8
10 -1 11 -1

output

42

input

4
-1 2 1 2
-1 0 1 0
-1 0 0 3
0 3 1 0

output

7

The image for the first example:

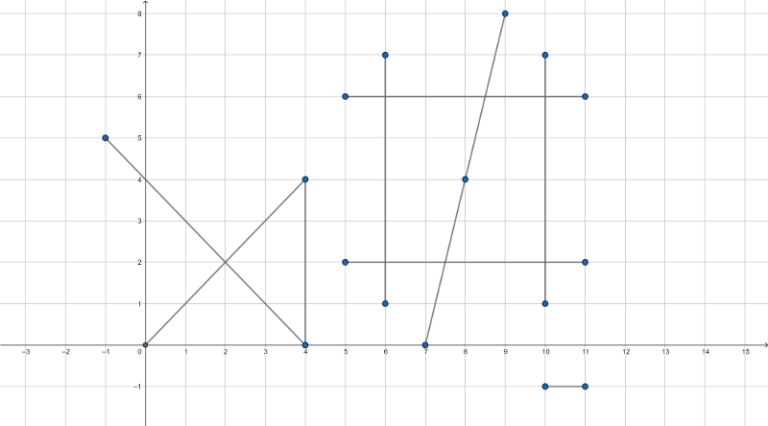
Several key points are marked blue, the answer contains some non-marked points as well.

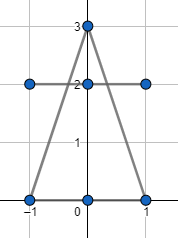
The image for the second example:

求线段进过的整数点。线段经过的点，为x轴长度，与y轴长度的gcd。

#include<bits/stdc++.h>
#define ll long long
using namespace std;

struct Point{
    ll x,y;
    Point(ll x=0,ll y=0):x(x),y(y){};
};

ll gcd(ll a,ll b)
{
    return a==0?b:gcd(b%a,a);
}

bool cheak(ll op1,ll a,ll b){
    if(a>b)
        swap(a,b);
    return op1>=a&&op1<=b;
}

Point point_of_intersection(Point f1,Point f2,Point f3,Point f4,bool &mark)
{
    ll a1,a2,b1,b2,c1,c2,c3,c4,D,D1,D2;
    a1=f2.y-f1.y;
    a2=f1.x-f2.x;
    b1=a1*f1.x+a2*f1.y;
    ///b1=(y2-y1)*x1+(x1-x2)*y1
    c1=f4.y-f3.y;
    c2=f3.x-f4.x;
    b2=c1*f3.x+c2*f3.y;
    ///b2=(y4-y3)*x3+(x3-x4)*y3
    c3=f2.x-f1.x;
    c4=f4.x-f3.x;

    D=c3*c1-c4*a1;
    Point res;
    if(D==0){
        mark=false;
        return res;
    }
    D1=b2*c3-b1*c4;
    if(D1%D){
        mark=false;
        return res;
    }
    res.x=int(D1/D);

    D2=b2*a1-b1*c1;
    if(D2%D){
        mark=false;
        return res;
    }
    res.y=int(D2/D);

    if(!cheak(res.x,f1.x,f2.x)||!cheak(res.x,f3.x,f4.x)){
        mark=false; return res;
    }
    if(!cheak(res.y,f1.y,f2.y)||!cheak(res.y,f3.y,f4.y)){
        mark=false; return res;
    }
    return res;
}

Point edge[1006][2];
int main()
{
    int n;
    while( ~scanf("%d",&n)){
        for(int i=1;i<=n;i++){
            scanf("%lld%lld%lld%lld",&edge[i][0].x,&edge[i][0].y,&edge[i][1].x,&edge[i][1].y);
        }

        set<pair<ll,ll> > re;
        long long ans=0,tmp;
        bool mark;
        for(int i=1;i<=n;i++){
            tmp=gcd(abs(edge[i][0].x-edge[i][1].x),abs(edge[i][0].y-edge[i][1].y))+1;
            re.clear();
            for(int j=1;j<i;j++){
                mark=true;
                Point res=point_of_intersection(edge[i][0],edge[i][1],edge[j][0],edge[j][1],mark);
                if(mark)
                    re.insert(make_pair(res.x,res.y));
            }
            ans+=tmp-re.size();
        }
        printf("%lld
",ans);
    }
    return 0;
}