二叉树的四种遍历方法（C++）

1.前序遍历

前序遍历：先遍历根节点，再遍历左子树，最后遍历右子树（根-左-右）

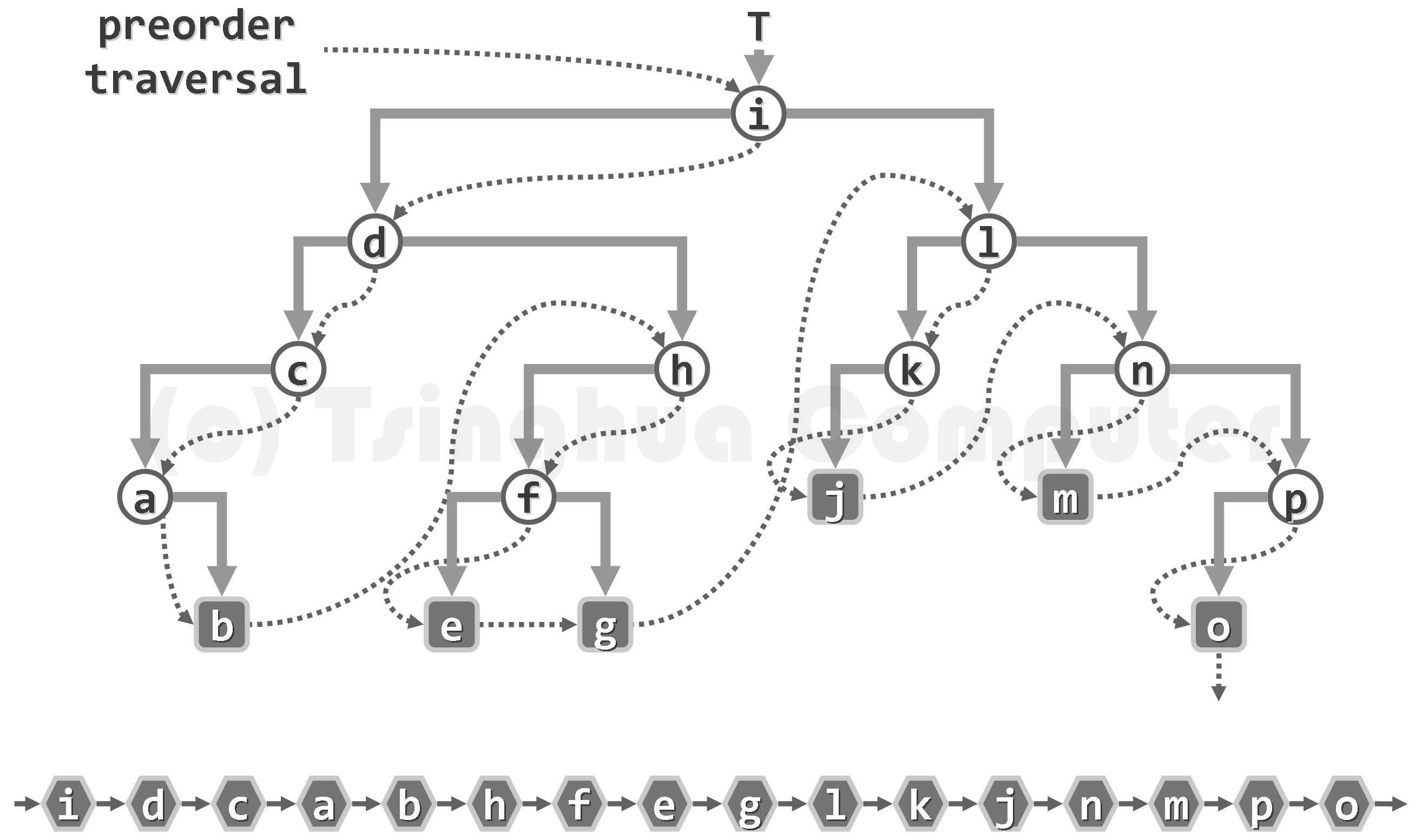
测试代码：

// 二叉树的三种遍历
// 1.前序遍历
// 2.中序遍历
// 3.后序遍历

#include <cstdio>
#include <stack>
#include <vector>
#include "BinaryTree.h"

using namespace std;

void visitAlongLeftBranch(BinaryTreeNode* , vector<int>& , stack<BinaryTreeNode*>&);

void TraverseBinaryTree(BinaryTreeNode* pRoot, vector<int>& treeNodes)  //二叉树前序遍历算法（迭代版）
{
    stack<BinaryTreeNode*> S; //辅助栈

    while (true)
    {
        visitAlongLeftBranch(pRoot, treeNodes, S);  //从当前节点逐批访问
        if (S.empty()) break; //栈为空, 弹出
        pRoot = S.top();  //弹出下一批的起点
        S.pop();
    }
}

//从当前节点出发, 沿左分支不断深入, 直至没有左分支的节点; 沿途节点遇到后立即访问
void visitAlongLeftBranch(BinaryTreeNode* pRoot, vector<int>& treeNodes, stack<BinaryTreeNode*>& S)
{
    while (pRoot)
    {
        treeNodes.push_back(pRoot->m_nValue); //访问当前节点
        S.push(pRoot->m_pRight); //右子节点入栈暂存
        pRoot = pRoot->m_pLeft; //沿左分支深入一层
    }
}

// ====================测试代码====================
void Test(const char* testName, BinaryTreeNode* pRoot, 
    vector<int> expectedPre, vector<int> expectedIn, vector<int> expectedPost, int expectedLength)
{
    if (testName != nullptr)
        printf("%s begins: ", testName);

    vector<int> treeNodes;  //保存遍历值
    TraverseBinaryTree(pRoot, treeNodes);
    int length = treeNodes.size();

    bool flag = true;  //标志位
    if (length != expectedLength) flag = false;  //长度不一致, 则遍历算法错误

    for (int i = 0; i < length; ++i)  //顺序不一致, 则遍历算法错误
    {
        if (treeNodes[i] != expectedPre[i])  //注意：遍历期望值在这里改
            flag = false;
    }
    
    if (flag)
        printf("Passed.");
    else
        printf("Failed.");

    //打印遍历值
    printf("
Expected: ");
    for (int i = 0; i < expectedLength; ++i)
        printf("%d ", expectedPre[i]);  //注意：遍历期望值在这里改

    printf("
Actual:   ");
    for (int i = 0; i < length; ++i)
        printf("%d ", treeNodes[i]);
    printf("

");
}

// 1.满二叉树
//            10
//          /    
//         6      14
//        /      /
//       4  8   12  16
void Test1()
{
    BinaryTreeNode* pNode10 = CreateBinaryTreeNode(10);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode14 = CreateBinaryTreeNode(14);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode8 = CreateBinaryTreeNode(8);
    BinaryTreeNode* pNode12 = CreateBinaryTreeNode(12);
    BinaryTreeNode* pNode16 = CreateBinaryTreeNode(16);

    ConnectTreeNodes(pNode10, pNode6, pNode14);
    ConnectTreeNodes(pNode6, pNode4, pNode8);
    ConnectTreeNodes(pNode14, pNode12, pNode16);

    vector<int> expectedPre = {10, 6, 4, 8, 14, 12, 16};
    vector<int> expectedIn = {4, 6, 8, 10, 12, 14, 16};
    vector<int> expectedPost = {4, 8, 6, 12, 16, 14, 10};

    Test("Test1", pNode10, expectedPre, expectedIn, expectedPost, 7);

    DestroyTree(pNode10);
}

// 2.完全二叉树
//            10
//          /    
//         6      14
//        /      /
//       4  8   12
void Test2()
{
    BinaryTreeNode* pNode10 = CreateBinaryTreeNode(10);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode14 = CreateBinaryTreeNode(14);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode8 = CreateBinaryTreeNode(8);
    BinaryTreeNode* pNode12 = CreateBinaryTreeNode(12);

    ConnectTreeNodes(pNode10, pNode6, pNode14);
    ConnectTreeNodes(pNode6, pNode4, pNode8);
    ConnectTreeNodes(pNode14, pNode12, nullptr);

    vector<int> expectedPre = { 10, 6, 4, 8, 14, 12};
    vector<int> expectedIn = { 4, 6, 8, 10, 12, 14};
    vector<int> expectedPost = { 4, 8, 6, 12, 14, 10 };

    Test("Test2", pNode10, expectedPre, expectedIn, expectedPost, 6);

    DestroyTree(pNode10);
}

// 3.二叉树
//            10
//          /    
//         6      14
//               /
//          8   12  
//         /
//        4
void Test3()
{
    BinaryTreeNode* pNode10 = CreateBinaryTreeNode(10);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode14 = CreateBinaryTreeNode(14);
    BinaryTreeNode* pNode8 = CreateBinaryTreeNode(8);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode12 = CreateBinaryTreeNode(12);

    ConnectTreeNodes(pNode10, pNode6, pNode14);
    ConnectTreeNodes(pNode6, nullptr , pNode8);
    ConnectTreeNodes(pNode8, pNode4, nullptr);
    ConnectTreeNodes(pNode14, pNode12, nullptr);

    vector<int> expectedPre = { 10, 6, 8, 4, 14, 12 };
    vector<int> expectedIn = { 6, 4, 8, 10, 12, 14 };
    vector<int> expectedPost = { 4, 8, 6, 12, 14, 10 };

    Test("Test3", pNode10, expectedPre, expectedIn, expectedPost, 6);

    DestroyTree(pNode10);
}

// 4.只有最左侧通路
//               5
//              /
//             4
//            /
//           3
//          /
//         2
//        /
//       1
void Test4()
{
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);

    ConnectTreeNodes(pNode5, pNode4, nullptr);
    ConnectTreeNodes(pNode4, pNode3, nullptr);
    ConnectTreeNodes(pNode3, pNode2, nullptr);
    ConnectTreeNodes(pNode2, pNode1, nullptr);

    vector<int> expectedPre = {5, 4, 3, 2, 1};
    vector<int> expectedIn = {1, 2, 3, 4, 5};
    vector<int> expectedPost = {1, 2, 3, 4, 5};

    Test("Test4", pNode5, expectedPre, expectedIn, expectedPost, 5);

    DestroyTree(pNode5);
}

// 4.只有最右侧通路
// 1
//  
//   2
//    
//     3
//      
//       4
//        
//         5
void Test5()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);

    ConnectTreeNodes(pNode1, nullptr, pNode2);
    ConnectTreeNodes(pNode2, nullptr, pNode3);
    ConnectTreeNodes(pNode3, nullptr, pNode4);
    ConnectTreeNodes(pNode4, nullptr, pNode5);

    vector<int> expectedPre = {1, 2, 3, 4, 5};
    vector<int> expectedIn = { 1, 2, 3, 4, 5 };
    vector<int> expectedPost = {5, 4, 3, 2, 1};

    Test("Test5", pNode1, expectedPre, expectedIn, expectedPost, 5);

    DestroyTree(pNode1);
}

// 树中只有1个结点
void Test6()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);

    vector<int> expectedPre = {1};
    vector<int> expectedIn = {1};
    vector<int> expectedPost = {1};

    Test("Test6", pNode1, expectedPre, expectedIn, expectedPost, 1);

    DestroyTree(pNode1);
}

// 树中没有结点
void Test7()
{
    vector<int> expectedPre = {};
    vector<int> expectedIn = {};
    vector<int> expectedPost = {};

    Test("Test7", nullptr, expectedPre, expectedIn, expectedPost, 0);
}

int main(int argc, char* argv[])
{
    Test1();
    Test2();
    Test3();
    Test4();
    Test5();
    Test6();
    Test7();

    return 0;
}

1.1 基于递归实现

void TraverseBinaryTree(BinaryTreeNode* pRoot, vector<int>& treeNodes)  //二叉树前序遍历算法（递归版）
{
    if (pRoot == nullptr)
        return;

    treeNodes.push_back(pRoot->m_nValue);
    TraverseBinaryTree(pRoot->m_pLeft, treeNodes);
    TraverseBinaryTree(pRoot->m_pRight, treeNodes);
}

1.2 基于迭代实现

 由于没有指向父节点的指针，所以需要辅助栈来记录路径中的右子节点。

void visitAlongLeftBranch(BinaryTreeNode* , vector<int>& , stack<BinaryTreeNode*>&);

void TraverseBinaryTree(BinaryTreeNode* pRoot, vector<int>& treeNodes)  //二叉树前序遍历算法（迭代版）
{
    stack<BinaryTreeNode*> S; //辅助栈

    while (true)
    {
        visitAlongLeftBranch(pRoot, treeNodes, S);  //从当前节点逐批访问
        if (S.empty()) break; //栈为空, 弹出
        pRoot = S.top();  //弹出下一批的起点
        S.pop();
    }
}

//从当前节点出发, 沿左分支不断深入, 直至没有左分支的节点; 沿途节点遇到后立即访问
void visitAlongLeftBranch(BinaryTreeNode* pRoot, vector<int>& treeNodes, stack<BinaryTreeNode*>& S)
{
    while (pRoot)
    {
        treeNodes.push_back(pRoot->m_nValue); //访问当前节点
        S.push(pRoot->m_pRight); //右子节点入栈暂存
        pRoot = pRoot->m_pLeft; //沿左分支深入一层
    }
}

 LeetCode

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        
        vector<int> ret;  //保存路径值
        stack<TreeNode*> S;  //辅助栈

        while (true)
        {
            if (root)  //寻找最左节点
            {
                ret.push_back(root->val);  //中途节点直接访问
                S.push(root->right);  //暂存右子节点
                root = root->left;
            }
            else if (!S.empty())
            {
                root = S.top(); S.pop();
            }
            else
                break;
        }
        return ret;
    }
};

2.中序遍历

中序遍历：先遍历左子树，再遍历根节点，最后遍历右子树（左-根-右）

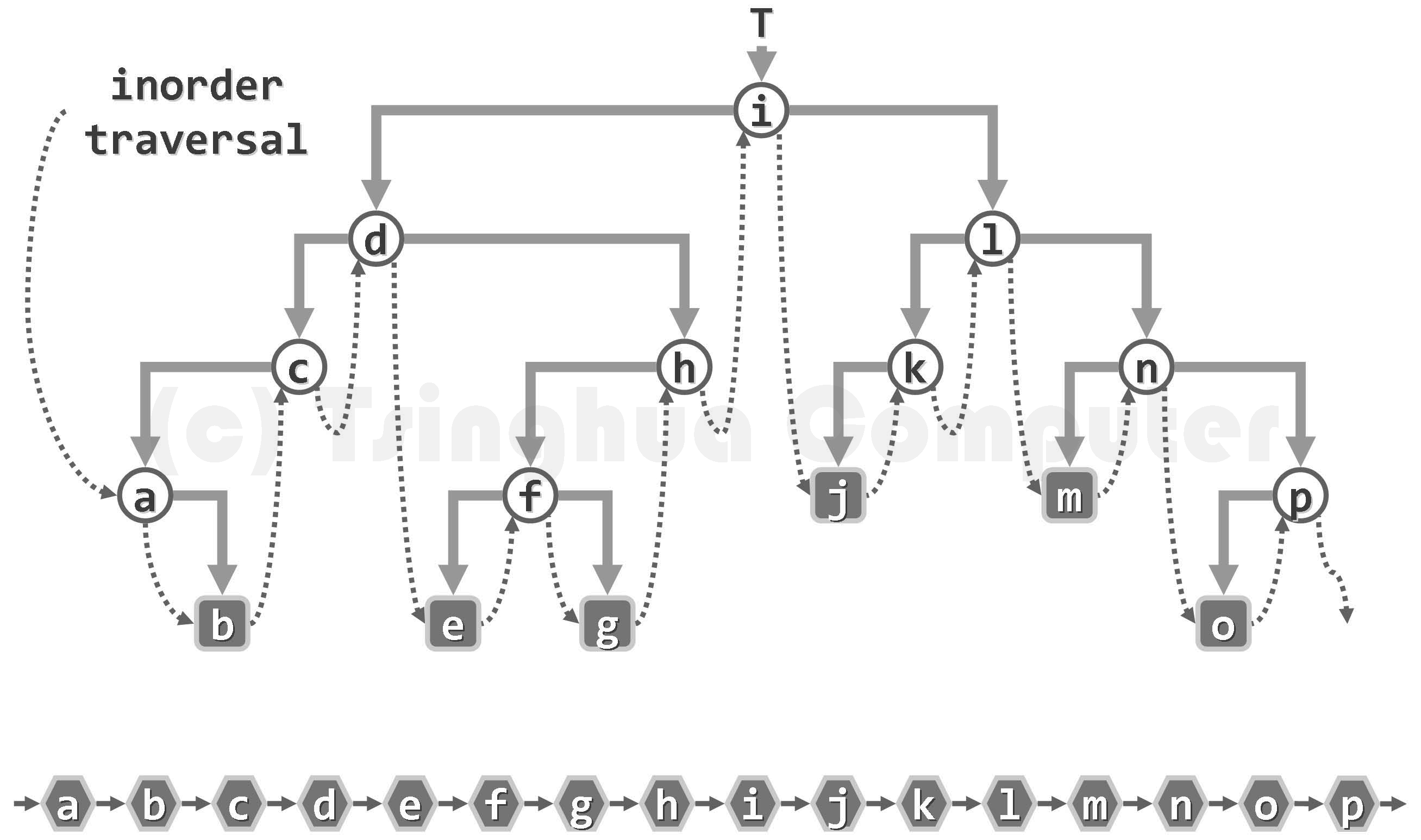
 测试代码：

// 二叉树的三种遍历
// 1.前序遍历
// 2.中序遍历
// 3.后序遍历

#include <cstdio>
#include <stack>
#include <vector>
#include "BinaryTree.h"

using namespace std;

void goAlongLeftBranch(BinaryTreeNode*, stack<BinaryTreeNode*>&);

void TraverseBinaryTree(BinaryTreeNode* pRoot, vector<int>& treeNodes)  //二叉树中序遍历算法（迭代版#1）
{
    stack<BinaryTreeNode*> S; //辅助栈

    while (true)
    {
        goAlongLeftBranch(pRoot, S);  //从当前节点出发,逐批入栈
        if (S.empty()) break;  //直至所有节点处理完毕
        pRoot = S.top();  //弹出栈顶节点并访问
        S.pop();
        treeNodes.push_back(pRoot->m_nValue);
        pRoot = pRoot->m_pRight;  //转向右子树
    }
}

//从当前节点出发, 沿左分支不断深入, 直至没有左分支的节点
void goAlongLeftBranch(BinaryTreeNode* pRoot, stack<BinaryTreeNode*>& S)
{
    while (pRoot) //当前节点入栈后随机向左侧分支深入, 迭代到无左子节点
    {
        S.push(pRoot);
        pRoot = pRoot->m_pLeft;
    }
}

// ====================测试代码====================
void Test(const char* testName, BinaryTreeNode* pRoot, 
    vector<int> expectedPre, vector<int> expectedIn, vector<int> expectedPost, int expectedLength)
{
    if (testName != nullptr)
        printf("%s begins: ", testName);

    vector<int> treeNodes;  //保存遍历值
    TraverseBinaryTree(pRoot, treeNodes);
    int length = treeNodes.size();

    bool flag = true;  //标志位
    if (length != expectedLength) flag = false;  //长度不一致, 则遍历算法错误

    for (int i = 0; i < length; ++i)  //顺序不一致, 则遍历算法错误
    {
        if (treeNodes[i] != expectedIn[i])  //注意：遍历期望值在这里改
            flag = false;
    }
    
    if (flag)
        printf("Passed.");
    else
        printf("Failed.");

    //打印遍历值
    printf("
Expected: ");
    for (int i = 0; i < expectedLength; ++i)
        printf("%d ", expectedIn[i]);  //注意：遍历期望值在这里改

    printf("
Actual:   ");
    for (int i = 0; i < length; ++i)
        printf("%d ", treeNodes[i]);
    printf("

");
}

// 1.满二叉树
//            10
//          /    
//         6      14
//        /      /
//       4  8   12  16
void Test1()
{
    BinaryTreeNode* pNode10 = CreateBinaryTreeNode(10);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode14 = CreateBinaryTreeNode(14);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode8 = CreateBinaryTreeNode(8);
    BinaryTreeNode* pNode12 = CreateBinaryTreeNode(12);
    BinaryTreeNode* pNode16 = CreateBinaryTreeNode(16);

    ConnectTreeNodes(pNode10, pNode6, pNode14);
    ConnectTreeNodes(pNode6, pNode4, pNode8);
    ConnectTreeNodes(pNode14, pNode12, pNode16);

    vector<int> expectedPre = {10, 6, 4, 8, 14, 12, 16};
    vector<int> expectedIn = {4, 6, 8, 10, 12, 14, 16};
    vector<int> expectedPost = {4, 8, 6, 12, 16, 14, 10};

    Test("Test1", pNode10, expectedPre, expectedIn, expectedPost, 7);

    DestroyTree(pNode10);
}

// 2.完全二叉树
//            10
//          /    
//         6      14
//        /      /
//       4  8   12
void Test2()
{
    BinaryTreeNode* pNode10 = CreateBinaryTreeNode(10);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode14 = CreateBinaryTreeNode(14);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode8 = CreateBinaryTreeNode(8);
    BinaryTreeNode* pNode12 = CreateBinaryTreeNode(12);

    ConnectTreeNodes(pNode10, pNode6, pNode14);
    ConnectTreeNodes(pNode6, pNode4, pNode8);
    ConnectTreeNodes(pNode14, pNode12, nullptr);

    vector<int> expectedPre = { 10, 6, 4, 8, 14, 12};
    vector<int> expectedIn = { 4, 6, 8, 10, 12, 14};
    vector<int> expectedPost = { 4, 8, 6, 12, 14, 10 };

    Test("Test2", pNode10, expectedPre, expectedIn, expectedPost, 6);

    DestroyTree(pNode10);
}

// 3.二叉树
//            10
//          /    
//         6      14
//               /
//          8   12  
//         /
//        4
void Test3()
{
    BinaryTreeNode* pNode10 = CreateBinaryTreeNode(10);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode14 = CreateBinaryTreeNode(14);
    BinaryTreeNode* pNode8 = CreateBinaryTreeNode(8);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode12 = CreateBinaryTreeNode(12);

    ConnectTreeNodes(pNode10, pNode6, pNode14);
    ConnectTreeNodes(pNode6, nullptr , pNode8);
    ConnectTreeNodes(pNode8, pNode4, nullptr);
    ConnectTreeNodes(pNode14, pNode12, nullptr);

    vector<int> expectedPre = { 10, 6, 8, 4, 14, 12 };
    vector<int> expectedIn = { 6, 4, 8, 10, 12, 14 };
    vector<int> expectedPost = { 4, 8, 6, 12, 14, 10 };

    Test("Test3", pNode10, expectedPre, expectedIn, expectedPost, 6);

    DestroyTree(pNode10);
}

// 4.只有最左侧通路
//               5
//              /
//             4
//            /
//           3
//          /
//         2
//        /
//       1
void Test4()
{
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);

    ConnectTreeNodes(pNode5, pNode4, nullptr);
    ConnectTreeNodes(pNode4, pNode3, nullptr);
    ConnectTreeNodes(pNode3, pNode2, nullptr);
    ConnectTreeNodes(pNode2, pNode1, nullptr);

    vector<int> expectedPre = {5, 4, 3, 2, 1};
    vector<int> expectedIn = {1, 2, 3, 4, 5};
    vector<int> expectedPost = {1, 2, 3, 4, 5};

    Test("Test4", pNode5, expectedPre, expectedIn, expectedPost, 5);

    DestroyTree(pNode5);
}

// 4.只有最右侧通路
// 1
//  
//   2
//    
//     3
//      
//       4
//        
//         5
void Test5()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);

    ConnectTreeNodes(pNode1, nullptr, pNode2);
    ConnectTreeNodes(pNode2, nullptr, pNode3);
    ConnectTreeNodes(pNode3, nullptr, pNode4);
    ConnectTreeNodes(pNode4, nullptr, pNode5);

    vector<int> expectedPre = {1, 2, 3, 4, 5};
    vector<int> expectedIn = { 1, 2, 3, 4, 5 };
    vector<int> expectedPost = {5, 4, 3, 2, 1};

    Test("Test5", pNode1, expectedPre, expectedIn, expectedPost, 5);

    DestroyTree(pNode1);
}

// 树中只有1个结点
void Test6()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);

    vector<int> expectedPre = {1};
    vector<int> expectedIn = {1};
    vector<int> expectedPost = {1};

    Test("Test6", pNode1, expectedPre, expectedIn, expectedPost, 1);

    DestroyTree(pNode1);
}

// 树中没有结点
void Test7()
{
    vector<int> expectedPre = {};
    vector<int> expectedIn = {};
    vector<int> expectedPost = {};

    Test("Test7", nullptr, expectedPre, expectedIn, expectedPost, 0);
}

int main(int argc, char* argv[])
{
    Test1();
    Test2();
    Test3();
    Test4();
    Test5();
    Test6();
    Test7();

    return 0;
}

2.1 基于递归实现

void TraverseBinaryTree(BinaryTreeNode* pRoot, vector<int>& treeNodes)  //二叉树中序遍历算法（递归版）
{
    if (pRoot == nullptr)
        return;

    TraverseBinaryTree(pRoot->m_pLeft, treeNodes);
    treeNodes.push_back(pRoot->m_nValue);
    TraverseBinaryTree(pRoot->m_pRight, treeNodes);
}

2.2 基于迭代实现

void goAlongLeftBranch(BinaryTreeNode*, stack<BinaryTreeNode*>&);

void TraverseBinaryTree(BinaryTreeNode* pRoot, vector<int>& treeNodes)  //二叉树中序遍历算法（迭代版#1）
{
    stack<BinaryTreeNode*> S; //辅助栈

    while (true)
    {
        goAlongLeftBranch(pRoot, S);  //从当前节点出发,逐批入栈
        if (S.empty()) break;  //直至所有节点处理完毕
        pRoot = S.top();  //弹出栈顶节点并访问
        S.pop();
        treeNodes.push_back(pRoot->m_nValue);
        pRoot = pRoot->m_pRight;  //转向右子树
    }
}

//从当前节点出发, 沿左分支不断深入, 直至没有左分支的节点
void goAlongLeftBranch(BinaryTreeNode* pRoot, stack<BinaryTreeNode*>& S)
{
    while (pRoot) //当前节点入栈后随即向左侧分支深入, 迭代到无左子节点
    {
        S.push(pRoot);
        pRoot = pRoot->m_pLeft;
    }
}

void TraverseBinaryTree(BinaryTreeNode* pRoot, vector<int>& treeNodes)  //二叉树中序遍历算法（迭代版#2）
{
    stack<BinaryTreeNode*> S; //辅助栈

    while (true)
    {
        if (pRoot)
        {
            S.push(pRoot);  //根节点进栈
            pRoot = pRoot->m_pLeft;  //深入遍历左子树
        }
        else if (!S.empty())
        {
            pRoot = S.top();  //尚未访问的最低祖先节点退栈
            S.pop();
            treeNodes.push_back(pRoot->m_nValue);
            pRoot = pRoot->m_pRight;  //转向右子树
        }
        else
            break;
    }
}

3. 后序遍历

后序遍历：先遍历左子树，再遍历右子树，最后遍历根节点（左-右-根）

 测试代码：

// 二叉树的三种遍历
// 1.前序遍历
// 2.中序遍历
// 3.后序遍历

#include <cstdio>
#include <stack>
#include <vector>
#include "BinaryTree.h"

using namespace std;

void gotoHLVFL(stack<BinaryTreeNode*>&);

void TraverseBinaryTree(BinaryTreeNode* pRoot, vector<int>& treeNodes)  //二叉树后序遍历算法（迭代版）
{
    stack<BinaryTreeNode*> S; //辅助栈

    if (pRoot)
        S.push(pRoot);  //根节点进栈

    while (!S.empty())
    {
        if ((S.top()->m_pLeft != pRoot)  // 若栈顶非当前节点的父节点（必为其右兄）
            && (S.top()->m_pRight != pRoot))  // 在以其右兄为根的子树中, 找到HLVFL
            gotoHLVFL(S);

        pRoot = S.top(); S.pop();
        if (pRoot)
            treeNodes.push_back(pRoot->m_nValue);
    }
}

// 在以S栈顶节点为根的子树中, 找到最高左侧可见节点
void gotoHLVFL(stack<BinaryTreeNode*>& S)
{
    while (BinaryTreeNode* pRoot = S.top())  // 自顶向下, 反复检查当前节点（即栈顶）
    {
        if (pRoot->m_pLeft) // 尽可能向左
        {
            if (pRoot->m_pRight)  //若有右子节点, 优先入栈
                S.push(pRoot->m_pRight);
            S.push(pRoot->m_pLeft);  //然后转入左子节点
        }
        else  //只有右子节点
            S.push(pRoot->m_pRight);
    }
    S.pop();
}


// ====================测试代码====================
void Test(const char* testName, BinaryTreeNode* pRoot, 
    vector<int> expectedPre, vector<int> expectedIn, vector<int> expectedPost, int expectedLength)
{
    if (testName != nullptr)
        printf("%s begins: ", testName);

    vector<int> treeNodes;  //保存遍历值
    TraverseBinaryTree(pRoot, treeNodes);
    int length = treeNodes.size();

    bool flag = true;  //标志位
    if (length != expectedLength) flag = false;  //长度不一致, 则遍历算法错误

    for (int i = 0; i < length; ++i)  //顺序不一致, 则遍历算法错误
    {
        if (treeNodes[i] != expectedPost[i])  //注意：遍历期望值在这里改
            flag = false;
    }
    
    if (flag)
        printf("Passed.");
    else
        printf("Failed.");

    //打印遍历值
    printf("
Expected: ");
    for (int i = 0; i < expectedLength; ++i)
        printf("%d ", expectedPost[i]);  //注意：遍历期望值在这里改

    printf("
Actual:   ");
    for (int i = 0; i < length; ++i)
        printf("%d ", treeNodes[i]);
    printf("

");
}

// 1.满二叉树
//            10
//          /    
//         6      14
//        /      /
//       4  8   12  16
void Test1()
{
    BinaryTreeNode* pNode10 = CreateBinaryTreeNode(10);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode14 = CreateBinaryTreeNode(14);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode8 = CreateBinaryTreeNode(8);
    BinaryTreeNode* pNode12 = CreateBinaryTreeNode(12);
    BinaryTreeNode* pNode16 = CreateBinaryTreeNode(16);

    ConnectTreeNodes(pNode10, pNode6, pNode14);
    ConnectTreeNodes(pNode6, pNode4, pNode8);
    ConnectTreeNodes(pNode14, pNode12, pNode16);

    vector<int> expectedPre = {10, 6, 4, 8, 14, 12, 16};
    vector<int> expectedIn = {4, 6, 8, 10, 12, 14, 16};
    vector<int> expectedPost = {4, 8, 6, 12, 16, 14, 10};

    Test("Test1", pNode10, expectedPre, expectedIn, expectedPost, 7);

    DestroyTree(pNode10);
}

// 2.完全二叉树
//            10
//          /    
//         6      14
//        /      /
//       4  8   12
void Test2()
{
    BinaryTreeNode* pNode10 = CreateBinaryTreeNode(10);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode14 = CreateBinaryTreeNode(14);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode8 = CreateBinaryTreeNode(8);
    BinaryTreeNode* pNode12 = CreateBinaryTreeNode(12);

    ConnectTreeNodes(pNode10, pNode6, pNode14);
    ConnectTreeNodes(pNode6, pNode4, pNode8);
    ConnectTreeNodes(pNode14, pNode12, nullptr);

    vector<int> expectedPre = { 10, 6, 4, 8, 14, 12};
    vector<int> expectedIn = { 4, 6, 8, 10, 12, 14};
    vector<int> expectedPost = { 4, 8, 6, 12, 14, 10 };

    Test("Test2", pNode10, expectedPre, expectedIn, expectedPost, 6);

    DestroyTree(pNode10);
}

// 3.二叉树
//            10
//          /    
//         6      14
//               /
//          8   12  
//         /
//        4
void Test3()
{
    BinaryTreeNode* pNode10 = CreateBinaryTreeNode(10);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode14 = CreateBinaryTreeNode(14);
    BinaryTreeNode* pNode8 = CreateBinaryTreeNode(8);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode12 = CreateBinaryTreeNode(12);

    ConnectTreeNodes(pNode10, pNode6, pNode14);
    ConnectTreeNodes(pNode6, nullptr , pNode8);
    ConnectTreeNodes(pNode8, pNode4, nullptr);
    ConnectTreeNodes(pNode14, pNode12, nullptr);

    vector<int> expectedPre = { 10, 6, 8, 4, 14, 12 };
    vector<int> expectedIn = { 6, 4, 8, 10, 12, 14 };
    vector<int> expectedPost = { 4, 8, 6, 12, 14, 10 };

    Test("Test3", pNode10, expectedPre, expectedIn, expectedPost, 6);

    DestroyTree(pNode10);
}

// 4.只有最左侧通路
//               5
//              /
//             4
//            /
//           3
//          /
//         2
//        /
//       1
void Test4()
{
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);

    ConnectTreeNodes(pNode5, pNode4, nullptr);
    ConnectTreeNodes(pNode4, pNode3, nullptr);
    ConnectTreeNodes(pNode3, pNode2, nullptr);
    ConnectTreeNodes(pNode2, pNode1, nullptr);

    vector<int> expectedPre = {5, 4, 3, 2, 1};
    vector<int> expectedIn = {1, 2, 3, 4, 5};
    vector<int> expectedPost = {1, 2, 3, 4, 5};

    Test("Test4", pNode5, expectedPre, expectedIn, expectedPost, 5);

    DestroyTree(pNode5);
}

// 4.只有最右侧通路
// 1
//  
//   2
//    
//     3
//      
//       4
//        
//         5
void Test5()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);

    ConnectTreeNodes(pNode1, nullptr, pNode2);
    ConnectTreeNodes(pNode2, nullptr, pNode3);
    ConnectTreeNodes(pNode3, nullptr, pNode4);
    ConnectTreeNodes(pNode4, nullptr, pNode5);

    vector<int> expectedPre = {1, 2, 3, 4, 5};
    vector<int> expectedIn = { 1, 2, 3, 4, 5 };
    vector<int> expectedPost = {5, 4, 3, 2, 1};

    Test("Test5", pNode1, expectedPre, expectedIn, expectedPost, 5);

    DestroyTree(pNode1);
}

// 树中只有1个结点
void Test6()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);

    vector<int> expectedPre = {1};
    vector<int> expectedIn = {1};
    vector<int> expectedPost = {1};

    Test("Test6", pNode1, expectedPre, expectedIn, expectedPost, 1);

    DestroyTree(pNode1);
}

// 树中没有结点
void Test7()
{
    vector<int> expectedPre = {};
    vector<int> expectedIn = {};
    vector<int> expectedPost = {};

    Test("Test7", nullptr, expectedPre, expectedIn, expectedPost, 0);
}

int main(int argc, char* argv[])
{
    Test1();
    Test2();
    Test3();
    Test4();
    Test5();
    Test6();
    Test7();

    return 0;
}

3.1 基于递归实现

void TraverseBinaryTree(BinaryTreeNode* pRoot, vector<int>& treeNodes)  //二叉树后序遍历算法（递归版）
{
    if (pRoot == nullptr)
        return;

    //后序遍历
    TraverseBinaryTree(pRoot->m_pLeft, treeNodes);
    TraverseBinaryTree(pRoot->m_pRight, treeNodes);
    treeNodes.push_back(pRoot->m_nValue);
}

3.2 基于迭代实现

void gotoHLVFL(stack<BinaryTreeNode*>&);

void TraverseBinaryTree(BinaryTreeNode* pRoot, vector<int>& treeNodes)  //二叉树后序遍历算法（迭代版）
{
    stack<BinaryTreeNode*> S; //辅助栈

    if (pRoot)
        S.push(pRoot);  //根节点进栈

    while (!S.empty())
    {
        if ((S.top()->m_pLeft != pRoot)  // 若栈顶非当前节点的父节点（必为其右兄）
            && (S.top()->m_pRight != pRoot))  // 在以其右兄为根的子树中, 找到HLVFL
            gotoHLVFL(S);

        pRoot = S.top(); S.pop();
        if (pRoot)
            treeNodes.push_back(pRoot->m_nValue);
    }
}

// 在以S栈顶节点为根的子树中, 找到最高左侧可见节点
void gotoHLVFL(stack<BinaryTreeNode*>& S)
{
    while (BinaryTreeNode* pRoot = S.top())  // 自顶向下, 反复检查当前节点（即栈顶）
    {
        if (pRoot->m_pLeft) // 尽可能向左
        {
            if (pRoot->m_pRight)  //若有右子节点, 优先入栈
                S.push(pRoot->m_pRight);
            S.push(pRoot->m_pLeft);  //然后转入左子节点
        }
        else  //只有右子节点
            S.push(pRoot->m_pRight);
    }
    S.pop();
}

4. 层次遍历

void TraverseBinaryTree(BinaryTreeNode* pRoot, vector<int>& treeNodes)  //二叉树层次遍历算法（迭代版）
{
    queue<BinaryTreeNode*> Q; //辅助栈

    Q.push(pRoot);  //根节点进栈

    while (!Q.empty())  //队列变空之前反复迭代
    {
        BinaryTreeNode* pRoot = Q.front();  //取出首节点并访问
        treeNodes.push_back(pRoot->m_nValue);

        if (pRoot->m_pLeft)
            Q.push(pRoot->m_pLeft);

        if (pRoot->m_pRight)
            Q.push(pRoot->m_pRight);
    }
}

可以参考之字形打印二叉树

https://www.cnblogs.com/ZSY-blog/p/12602375.html

调用代码：

//==================================================================
// 《剑指Offer——名企面试官精讲典型编程题》代码
// 作者：何海涛
//==================================================================

#pragma once

struct BinaryTreeNode 
{
    int                    m_nValue; //节点data值
    BinaryTreeNode*        m_pLeft;  //左子节点
    BinaryTreeNode*        m_pRight; //右子节点
};

__declspec( dllexport ) BinaryTreeNode* CreateBinaryTreeNode(int value);
__declspec( dllexport ) void ConnectTreeNodes(BinaryTreeNode* pParent, BinaryTreeNode* pLeft, BinaryTreeNode* pRight);
__declspec( dllexport ) void PrintTreeNode(const BinaryTreeNode* pNode);
__declspec( dllexport ) void PrintTree(const BinaryTreeNode* pRoot);
__declspec( dllexport ) void DestroyTree(BinaryTreeNode* pRoot);

//==================================================================
// 《剑指Offer——名企面试官精讲典型编程题》代码
// 作者：何海涛
//==================================================================

#include <cstdio>
#include "BinaryTree.h"

//新建一个父节点
BinaryTreeNode* CreateBinaryTreeNode(int value)
{
    BinaryTreeNode* pNode = new BinaryTreeNode();
    pNode->m_nValue = value;
    pNode->m_pLeft = nullptr;
    pNode->m_pRight = nullptr;

    return pNode;
}

//父节点连接左右子节点
void ConnectTreeNodes(BinaryTreeNode* pParent, BinaryTreeNode* pLeft, BinaryTreeNode* pRight)
{
    if(pParent != nullptr)
    {
        pParent->m_pLeft = pLeft;
        pParent->m_pRight = pRight;
    }
}

//打印当前父节点以及左右子节点
void PrintTreeNode(const BinaryTreeNode* pNode)
{
    if(pNode != nullptr)
    {
        printf("value of this node is: %d
", pNode->m_nValue);

        if(pNode->m_pLeft != nullptr)
            printf("value of its left child is: %d.
", pNode->m_pLeft->m_nValue);
        else
            printf("left child is nullptr.
");

        if(pNode->m_pRight != nullptr)
            printf("value of its right child is: %d.
", pNode->m_pRight->m_nValue);
        else
            printf("right child is nullptr.
");
    }
    else
    {
        printf("this node is nullptr.
");
    }

    printf("
");
}

//递归调用打印整个二叉树
void PrintTree(const BinaryTreeNode* pRoot)
{
    PrintTreeNode(pRoot);

    if(pRoot != nullptr)
    {
        if(pRoot->m_pLeft != nullptr)
            PrintTree(pRoot->m_pLeft);

        if(pRoot->m_pRight != nullptr)
            PrintTree(pRoot->m_pRight);
    }
}

//递归调用删除整个树
void DestroyTree(BinaryTreeNode* pRoot)
{
    if(pRoot != nullptr)
    {
        BinaryTreeNode* pLeft = pRoot->m_pLeft;
        BinaryTreeNode* pRight = pRoot->m_pRight;

        delete pRoot;
        pRoot = nullptr;

        DestroyTree(pLeft);
        DestroyTree(pRight);
    }
}

代码与图参考：

[1] 剑指offer（第二版）, 何海涛, 2011.

[2] 数据结构（C++语言版）, 邓俊辉, 2010.