今天,$zutter$终于下定决心去学了数论,然后

从基础说起
-
gcd
这个..感性理解一下就好了啊
gcd(int a,int b)
{
if(b==0) return a;
return(b,a%b);
}
证明:
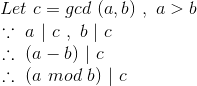
-
exgcd
扩展欧几里得算法,用于在已知(a,b)时求解(x,y) 使 a*x+b*y=c (c | gcd(a,b))
int ex_gcd(int a,int b,int &x,int &y)
{
int ret, tmp;
if(! b)
{
x = 1, y = 0;
return a;
}
ret=ex_gcd(b, a % b, x, y);
tmp= ; x=y; y=tmp-a/b*y;
return ret;
}
证明:
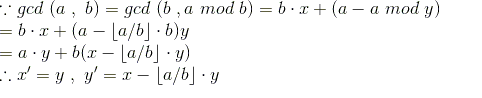
又因为 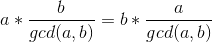
所以任意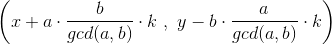 都可为解
都可为解
-
逆元
当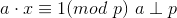 时,称x为a在%p意义下的逆元,记作
时,称x为a在%p意义下的逆元,记作 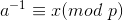
解法:
-
- 扩展欧几里得
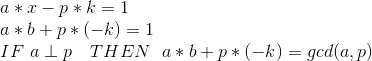
-
- 费马小定理
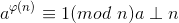 且
且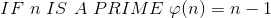
- 费马小定理
-
- 线性求逆元
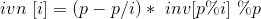
- 线性求逆元
-
中国剩余定理 Chinese Rimainder Theorem
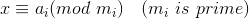
解法:
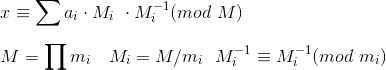
-
排列
求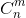 %P
%P
-
- $C_n^m=C_{n-1}^{m-1}+C_{n-1}^{m}$
- m,n小于p时可以用O(n)的时间预处理,用O(1) 求值
方法
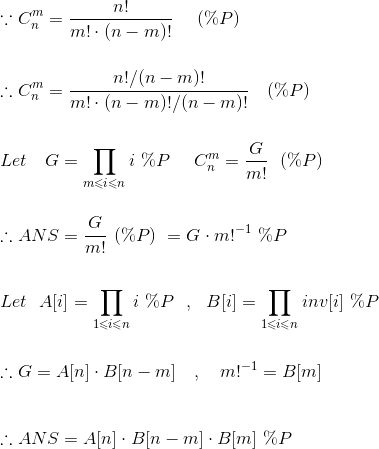
2.当m,n过大p过小,m,n>p 时
-
- 卢卡斯定理
求c的公式 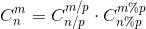
递归中每次当 m,n<p 时调用1中公式即可。
-
二项式定理
$(x+y)^n$ 中 $x^ty^{n-t}$ 的系数为 $C_n^t$