主席树模板

主席树模板 查静态区间第K小

首先考虑整个序列查第k大做法： 权值线段树
将序列以权值为下标存入线段树，每个节点存数字出现次数
栗子：序列 3 3 1 2 4 3 2 建成的权值线段树

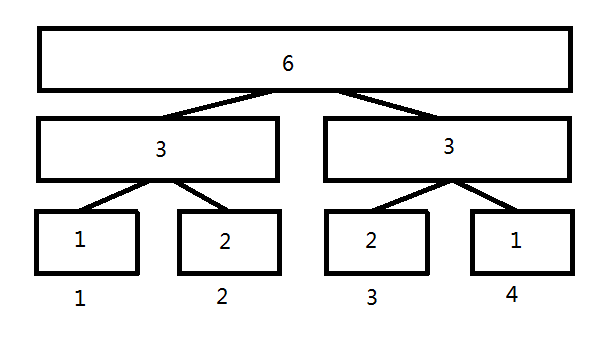
假如要找第3小的数

1. 说先访问根节点，发现根节点的左儿子正好有3个，进入左儿子
2. 在左儿子中找地3大，他的左儿子只有一个数所以访问右儿子找第(3-1)大
3. 此节点为根节点，直接返回值即可

---

而这道问题是求静态区间第k小，用前缀和思想对每个节点建立前缀可持久化权值线段树，然后每次查找 l 到 (r) 的区间第k小时只要用 r 的值减去 l-1 的值即为 l−r 的权值线段树，用上述方法直接查找即可

---

#include<iostream>
#include<stdio.h>
#include<algorithm>
#define M 200010
#define update(a) f[a]=f[ls[a]]+f[rs[a]]
using namespace std;

int cnt,i,m,n,j,k,a[M],b[M],pre[M],ls[M*20],rs[M*20],g[M],f[M],q,x,y,z;

void built1(int now,int l,int r)
{
	if(l==r) return;
	int mid=(l+r)>>1;
	cnt+=1; ls[now]=cnt;
	built1(cnt,l,mid);
	cnt+=1; rs[now]=cnt;
	built1(cnt,mid+1,r);
}

void built(int now,int l,int r,int z,int p)
{
	if(l==r) {f[now]=f[p]+1; return;}
	int mid=(l+r)>>1;
	if(z<=mid) 
	{
		rs[now]=rs[p]; ls[now]=++cnt;
		built(cnt,l,mid,z,ls[p]);
	}	
	else 
	{
		ls[now]=ls[p]; rs[now]=++cnt;
		built(cnt,mid+1,r,z,rs[p]);
	}
	update(now);
}

int search(int x,int y,int z,int l,int r)
{
	if(l==r) return l;
	int ll=f[ls[x]]-f[ls[y]], mid=(l+r)>>1;
	if(ll>=z) return search(ls[x],ls[y],z,l,mid);
	return search(rs[x],rs[y],z-ll,mid+1,r);
}

int main()
{
	scanf("%d%d",&n,&q);
	for(i=1;i<=n;++i) scanf("%d",&a[i]),b[i]=a[i];
	
	sort(b+1,b+1+n);
	m=unique(b+1,b+1+n)-b-1;
	for(i=1;i<=n;i++)
	{
		k=lower_bound(b+1,b+1+m,a[i])-b;
		pre[k]=a[i]; a[i]=k;
	}
	
	g[0]=cnt=1; 
	built1(1,1,m);
	for(i=1;i<=n;++i)
	{
		g[i]=++cnt;
		built(cnt,1,m,a[i],g[i-1]);
	}
	for(i=1;i<=q;i++) 
	{
		scanf("%d%d%d",&x,&y,&z);
		printf("%d
",pre[search(g[y],g[x-1],z,1,m)]);	
	}
}