字典树
定义
其本质就是用一颗树来记录大量的字符串,主要适用于长度较小但是个数较多的情况,是一种数据结构。其核心思想是在插入时充分利用已有的字符串,也就是合并不同字符串的公共前缀。字典树的主要功能就是查找,每次的查询只和字符串长度有关所以就是$O(1)$复杂度,又由于其结构可以用来求两个字符串的$lcp$。初始化操作的复杂度为$O(nl)$,$l$为字符串长度(网上没找到,但应该就是这个)。
实现
这里用的是基地里的王大佬的板子,代码中的$ch$数组就是树,第一维是树的层(我自己瞎叫的,区别于深度),第二维对应$26$个字母(当然可以扩充,只要改变一下宏定义里的$id$就可以了),$end$数组是记录第$i$个节点是否为一个字符串的末尾,先上代码:
1 struct Trie{
2 int tot,ch[maxn][30],end[maxn];
3 void init(){//#define cl(x) memset(x,0,sizeof(x))
4 cl(ch),cl(end),tot=1;
5 }
6 int append(int pos,int c){//在pos节点上插入编号为c('a'为0,依次往后)的字符
7 int &t=ch[pos][c];
8 return t?t:t=++tot;
9 }
10 int insert(string s){//#define id(x) (x-'a')
11 int pos=1,i;
12 for(int i=0;i<s.size();i++)
13 pos=append(pos,id(s[i]));
14 end[pos]++;
15 return pos;
16 }
17 bool find(string a){
18 ll u,v;
19 u=0;
20 for(int i=0;i<a.size();i++){
21 v=id(a[i]);
22 if(!ch[u][v]) return 0;
23 u=ch[u][v];
24 }
25 if(!end[u]) return 0;
26 return 1;
27 }
28 }tree;
前两个函数直接看的话不太清楚,这里给出一组输入输出结果就更清楚了:
1 input:
2 rfcytcu
3 rfcfe
4
5 output:
6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0
8 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
9 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 0 0 0 0 0 9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 0
11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0
12 0 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
13 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 8 0 0 0 0 0
14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
15 0 0 0 0 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
输出是$ch$数组,具体代码就不贴了。可以看到实际的$ch[0]$就是根节点所在的那一层。在查找的时候一开始将$pos$赋值为$1$,也就是从$ch[1]$开始查找,查找的位置就是字符串当前字符的编号,然后如果不为$0$就说明已经插入了该字符,那么就继续往下查找,查找的层数编号恰好就是这个非零的值。在查找的时候有三种情况:
1. 当走到被查找字符的末尾时恰好停止,此时判断$end[i]$如果不为$0$就说明这里是一个已经插入的字符说明字符存在;
2. 如果字符串已经结束但是还未到任何一个$end$非零的节点说明字符不存在;
3. 如果树已经到了一个尽头(就是后面没有子节点了),看到第$14$行,此时这一整行为$0$,那么就说明字符串不存在,这得益于在插入时的处理。
思考题
1. 求出整个集合中所有的公共前缀。
遍历整棵树(一开始脑抽了,以为遍历是指数的,因为要遍历的话要一层一层的循环,但其实由于总的个数是小于等于$n$的,所以其实复杂度是$O(26n)$的),画图知道其实就是总节点数减去叶子节点。用$dfs$每次如果有一行不为零就跳到那一行,如果这个下一行全为$0$就说明这是一个叶子;总节点数就是结构体里面的$tot$,然后就完了。
2. 给出一个字符串,问有多少字符串含有该前缀。
多开一个数组记录经过该节点的个数,然后改一下$find$函数,如果存在就返回经过该点的次数。
KMP算法
定义
$KMP$算法是一种改进的字符串匹配算法,其复杂度为$O(mn)$,$m,n$分别为主串长度和用于匹配的串的长度。在求解的过程中用到了$next$数组,该数组的定义是:一个字符串的前缀$pref_i$的最长公共前后缀的长度,就是首尾部分相同的最长子串(不包括本身),又由于在匹配过程中为了更加方便,所以一般$next_i$对应的是从第$0$号元素到第$i-1$号元素的值。
实现
$KMP$算法本身很简单,就是在移动指针的时候有目的的移动,每次移动到尽可能多的匹配字符的位置。主要是如何得到$next$数组,在网上看了好久,总是感觉讲的较为繁琐(可能是我不集中的问题,当然可能我讲的也很繁琐)。
如果根据定义直接求解的话肯定是不够优秀的,所以需要进行优化,这里使用的是双指针。
我们规定下标从$0$开始(网上也有从$1$开始,个人觉得从$0$开始便捷因为可以直接用字符串对象),这里使用两个指针(并不是那个指针只是代表一个位置)$j,k$。现在假设在某个位置如下所示:
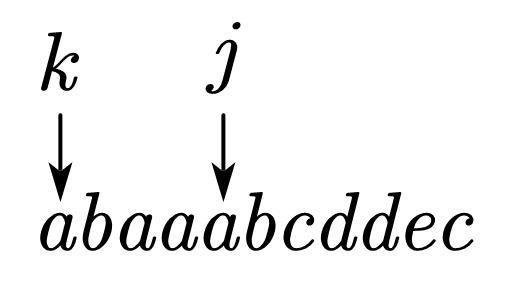
此时可以看到对应的$next_{j+1}$为$1$,接下来判断$s[j+1]$和$s[k+1]$,二者是相等的那么下一步就是:

而此时的$next_{j+1}$就是上一步的$next_{j+1}$自加$1$。然后继续判断,发现这次不相等了:
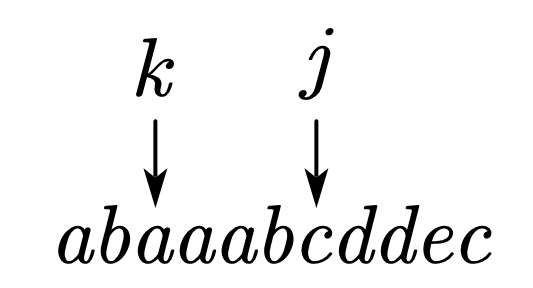
这里就相当于是原本大问题中的匹配失败,显然我们需要利用已有的$next$数组,这里其实就是返回$next_k$。这样就不全是直接回到初始位置,而是尽可能的判断是否有可以利用的信息,那么下一步就长这样:

这次的例子返回了以后就直接到了第一个位置,那么再次判断发现二者不相同,就要重复上述步骤。
重复当中,如果有相同的,那么就更新$next$的值;
如果最终到达了初始位置(就是这张图的样子),这时就出现了一个问题:根据定义,$next_0$是不存在的(因为就只到$i-1$号元素,而$-1$号是不存在的),如果此时将这个变量初始化为$0$就会出现死循环;定义为一个正数,有可能会影响结果;所以干脆定义成$-1$(其实任何在整个过程中不会出现的数字都可以,$-1$最为常见),这样就只需要再加入一个特判就可以实现,以上就是大概流程,接下来看一看代码然后再自己写一下就可以体会到了:
1 int nxt[maxn];
2 void getnext(string s){//下标从零开始
3 int j=0,k=-1,len=s.size();
4 nxt[0]=-1;
5 while(j<len){
6 if(k==-1||s[k]==s[j]){
7 nxt[++j]=++k;
8 }else k=nxt[k];
9 }
10 }
代码本身还是相当简单的,就$10$行。
思考题
1. 字符串匹配问题
$KMP$算法的初衷,可以找到目标串在主串中出现的次数和位置。大概的做法就是,在原本暴力的基础上,每次移动的位数和$next$挂钩,这样最终的复杂度是$O(n+m)$。
2. POJ 2406
题意:给出一个串,找出其最小循环节的个数。
分析:一开始想差了,以为是要求周期。利用$next$数组可知,如果一个串有循环节,那么循环节长度$=$总长度$-$next_n$。然后由于是循环节,那么一定有总长度可以整除循环节长度,然后就是裸题了。
3. 牛客15071 数一数
题意:给出若干串,定义$fleft( s,t ight) =$$s$在$t$中出现的次数,求出所有的$prod_{j=1}^n{fleft( s_i,s_j ight)}$。
分析:脑筋急转弯,其实$f$很容易等于$0$,只要前者比后者长就莫得了,所以给所有串排个序,只有长度最小的那些可能不等于$0$;如果最小长度有两个或以上的不同字符串,那就全等于$0$了;如果只有一个,那就用$KMP$算法$O(n)$求出次数再累乘就可。