1 算术指令
加法指令
ADD、ADC、INC
减法指令
SUB、SBB、DEC、NEG、CMP
乘法指令
MUL、IMUL
除法指令
DIV、IDIV
十进制调整指令
DAA、DAS、
AAA、AAS、AAM、AAD
2 加法指令
2.1指令
加法指令: ADD DST, SRC
执行操作: (DST) ← (SRC) + (DST)
带进位加法指令: ADC DST, SRC
执行操作: (DST) ← (SRC) + (DST) + CF
加1指令: INC OPR
执行操作: (OPR) ← (OPR) + 1
注意:
* 除INC指令不影响CF标志外,均对条件标志位有影响。
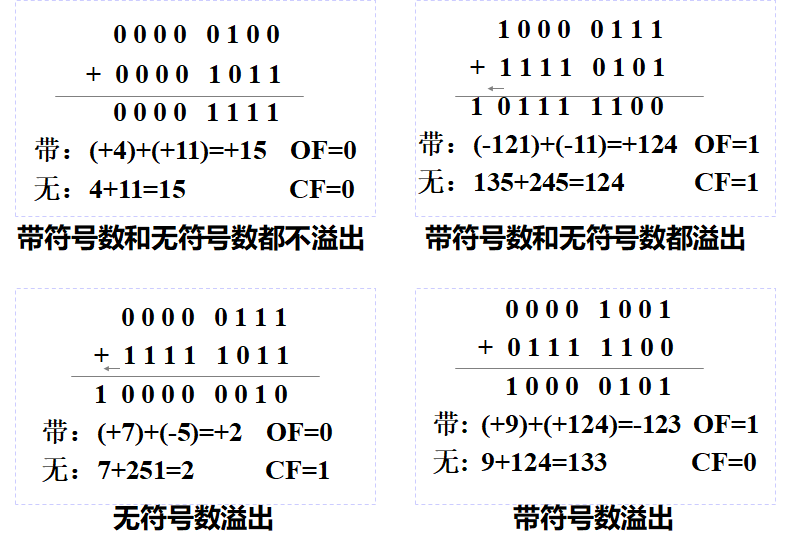
2.2 加法指令对条件标志位的影响

举例: n=8 bit 带符号数(-128~127) , 无符号数(0~255)
例:双精度数的加法
(DX) = 0002H (AX) = 0F365H
(BX) = 0005H (CX) = 8100H
指令序列 ADD AX, CX ; (1)
ADC DX, BX ; (2)
(1) 执行后,(AX) = 7465H
CF=1 OF=1 SF=0 ZF=0
(2) 执行后,(DX) = 0008H
CF=0 OF=0 SF=0 ZF=0
3减法指令
3.1指令
减法指令: SUB DST, SRC (subtract)
执行操作: (DST) ← (DST) - (SRC)
带借位减法指令: SBB DST, SRC (subtract with borrow)
执行操作: (DST) ← (DST) - (SRC) - CF
减1指令: DEC OPR (decrement)
执行操作: (OPR) ← (OPR) - 1
求补指令: NEG OPR (negate)
执行操作: (OPR) ← - (OPR) (OPR)← 0FFFF - (OPR)+ 2
把操作数按位求反后末位加一
比较指令: CMP OPR1, OPR2 (compare)
执行操作: (OPR1) - (OPR2)
注意:
* 除DEC指令不影响CF标志外,均对条件标志位有影响。
3.2对条件标志位(CF/OF/ZF/SF)的影响
3.2.1减法指令对条件标志位(CF/OF/ZF/SF)的影响

3.2.2NEG 指令对CF/OF的影响

例:x、y、z 均为双精度数,分别存放在地址为X, X+2;Y, Y+2;Z, Z+2的存储单元中,
用指令序列实现w ← x + y + 24 - z ,并用W, W+2单元存放w
MOV AX, X MOV DX, X+2 ADD AX, Y ADC DX, Y+2 ; x+y ADD AX, 24 ADC DX, 0 ; x+y+24 SUB AX, Z SBB DX, Z+2 ; x+y+24-z MOV W, AX MOV W+2, DX ; 结果存入W, W+2单元
4乘法指令
4.1指令
无符号数乘法指令: MUL SRC
带符号数乘法指令: IMUL SRC
执行操作:
字节操作数 (AX) ← (AL) * (SRC)
字操作数 (DX, AX) ← (AX) * (SRC)
注意:
* AL (AX) 为隐含的乘数寄存器。
* AX (DX,AX) 为隐含的乘积寄存器。
* SRC不能为立即数。
* 除CF和OF外,对条件标志位无定义
4.2乘法指令对 CF/OF 的影响

例:(AX) = 16A5H,(BX) = 0611H
(1) IMUL BL ; (AX) ← (AL) * (BL)
; A5*11 =》 5B*11=060B =》 F9F5
; (AX) = 0F9F5H CF=OF=1
(2) MUL BX ; (DX, AX) ← (AX) * (BX)
; 16A5*0611=0089 5EF5
; (DX)=0089H (AX)=5EF5H CF=OF=1
5.除法指令
5.1指令
无符号数除法指令: DIV SRC
带符号数除法指令: IDIV SRC
执行操作:
字节操作 (AL) ← (AX) / (SRC) 的商
(AH) ← (AX) / (SRC) 的余数
字操作 (AX) ← (DX, AX) / (SRC) 的商
(DX) ← (DX, AX) / (SRC) 的余数
注意:
* AX (DX,AX) 为隐含的被除数寄存器。
* AL (AX) 为隐含的商寄存器。
* AH (DX) 为隐含的余数寄存器。
* SRC不能为立即数。
* 对所有条件标志位均无定义。如何判别结果有效?
例:x , y , z , v 均为16位带符号数,计算
( v - ( x*y + z – 540 ) ) / x
MOV AX, X IMUL Y ; x*y →(DX,AX) MOV CX, AX MOV BX, DX MOV AX, Z CWD ;Z →(DX,AX) ADD CX, AX ADC BX, DX ; x*y+z →(BX,CX) SUB CX, 540 SBB BX, 0 ; x*y+z-540 MOV AX, V CWD ;V →(DX,AX) SUB AX, CX SBB DX, BX ; v-(x*y+z-540) IDIV X ; (v-(x*y+z-540))/x→(AX) 余数→(DX)
6.十进制调整指令
6.1BCD码
BCD码:用二进制编码的十进制数,又称二--十进制数 (binary code decimal)
压缩的BCD码:用 4 位二进制数表示 1 位十进制数
例:( 59 )10 =( 0101 1001 )BCD
非压缩的BCD码:用 8 位二进制数表示 1 位十进制数
例:( 59 )10 =( 0000 0101 0000 1001 )BCD
数字的 ASCII 码是一种 非压缩的 BCD 码
DIGIT ASCII BCD
0 30H 0011 0000
1 31H 0011 0001
2 32H 0011 0010
… … …
9 39H 0011 1001
例:写出( 3590 )10的压缩 BCD 码和非压缩BCD码,并分
别 把它们存入数据区 PAKED 和 UNPAK
压缩BCD: ( 3590 )10=( 0011 0101 1001 0000 )BCD
非压缩BCD:
( 3590 )10=( 00000011 00000101 00001001 00000000 )BCD

问题的提出:
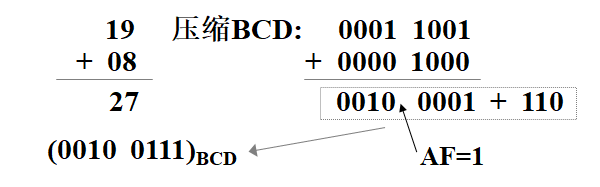
6.2指令
(1)压缩的BCD码调整指令
● DAA 加法的十进制调整指令 (decimal adjust for addition)
● DAS 减法的十进制调整指令(decimal adjust for subtraction)
(2)非压缩的BCD码调整指令
● AAA 加法的ASCII码调整指令 (ASCII adjust for addition)
● AAS 减法的ASCII码调整指令 (ASCII adjust for subtraction)
● AAM 乘法的ASCII码调整指令 (ASCII adjust for multiplication)
● AAD 除法的ASCII码调整指令 (ASCII adjust for devision)
压缩BCD运算举例: (1) MOV AL, BCD1 ; BCD1=34H ADD AL, BCD2 ; BCD2=59H, (AL)=8DH DAA ; 8DH+06H=93H MOV BCD3, AL ; BCD3=93H (2) MOV AL, BCD1 ; BCD1=34H SUB AL, BCD2 ; BCD2=59H , (AL)=0DBH DAS ; 0DBH-60H-06H=75H MOV BCD3, AL ; BCD3= 75 = - 25 (10^n’补码)
非压缩BCD运算举例: (1) MUL BL ; (AX)=(AL)×(BL)=08 × 09 AAM ; (AL)/0AH= 48H /0AH→ 0702 (2)AAD ; (AX) →(AH) ×0AH+(AL)=48H DIV BL ; (AL) = (AX)/(BL)=48H/4=12H AAM ; (AL)/0AH=12H/0AH=0108
