浮点数

浮点数

首发于https://zlogs.net,如果排版有问题，影响阅读，请到https://zlogs.net访问

不同时间段写的，不同参考，词语翻译不一样，下列词语是等价的

规格数=规范数=正规数

非规格数=非规范数=次正规数

怎么表示

数学中的数

• 数学中的数是怎么表示的，

  • 有两种方法，一种是普通计数如(12345)和(123.45)，还有一种是科学计数法，如(1.2345 imes10^4)和(1.2345 imes10^{-2})

  • 维基

    科学记数法（英语：Scientific notation，英国则称为 Standard form），又称为科学记数法或科学记法，是一种数字的表示法。科学记数法最早由阿基米德提出。

• 科学记数法有什么好处

  • 非常大数和非常小数表示时好处非常明显，可以很清晰看出量级和大小，如(123450000000000000000=1.2345 imes10^{20},0.00000000012345=1.2345 imes10^{-10})

  • 当我们要表示非常大或非常小的数时，如果用一般的方法，将一个数的所有位数都写出来，会很难直接确知它的大小，还会浪费很多空间。但若使用科学记数法，一个数的数量级、精确度和数值都较容易看出，例如于化学里，以公克表示一个质子质量的数值为:0.00000000000000000000000167262158, 但如果将它转成科学记数法的形式，便可不需要写那么多零︰(1.67262158 imes 10^{-24})，又例如，若以公斤为表示单位，则木星的质量值约为：1898130000000000000000000000

    像这样的大数亦无法直接用列出所有位数的方式表达出精确度，但科学记数法就能用下方形式明白的表示出来：

    (1.89813 imes 10^{27})

计算机中的数

• 计算机中的数也是类似，我们可以有多种存放方法，

  • 从这里开始下面就只讨论小数（浮点数）的存放方法

  • 比如0.00000000000000000000000167262158，可以先存数值本身即0 00000000000000000000000167262158，再存一个1表示小数点在哪，在第一个0的后面

  • 除了上面的存放方法还有其他存放方法，计算机发展初期对于小数还有各种各样的存法，各家制定各家规则的，互相不兼容，写程序还要写几套很麻烦，后来IEEE选择一个较好的制定成标准，以后大家都别各自搞各自的了，都按照这个来，这个标准就是IEEE754二进制浮点数算术标准

浮点表示对形如(V=x imes 2^y)的有理数进行编码。 它对执行涉及非常大的数字((|V|>>0))、非常接近于(0(|V|<<1))的数字， 以及更普遍地作为实数运算的近似值的计算， 是很有用的。
直到20世纪80年代， 每个计算机制造商都设计了自己的表示浮点数的规则， 以及对 浮点数执行运算的细节。 另外， 它们常常不会太多地关注运算的精确性，而把实现的速度 和简便性看得比数字梢确性更重要。
勹大约在1985年， 这些情况随看IEEE标准754的推出而改变了， 这是一个仔细制订的 表示浮点数及其运算的标准。 这项工作是从1976年开始由Intel赞助的， 与8087的设计 同时进行，8087是一种为8086处理器提供浮点支持的芯片。 他们请William Kahan(加州 大学伯克利分校的一位教授）作为顾问， 帮助设计未来处理器浮点标准。 他们支持Kahan 加入一个IEEE资助的制订工业标准的委员会。 这个委员会最终采纳的标准非常接近于 Kahan为Intel设计的标准。 目前， 实际上所有的计算机都支持这个后来被称为IEEE浮 点的标准。 这大大提高了科学应用程序在不同机器上的可移植性。

IEEE754转化过程

• IEEE754存储浮点数有点类似于十进制的科学记数法表示数

存储在32位的float里面，其中符号一位，尾数23位，指数8位

31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
s=sign	e=exponent(8 bits)								f=fraction(23 bit)

规格数

((-1)^{s} 10^{e-1111111} imes 1.f=(-1)^{s} 2^{e-127} imes 1.f)

非规格数

((-1)^{s} 10^{1-1111111} imes 0.f=(-1)^{s} 2^{1-127} imes 0.f)

规格数(10.5存储为例)

下面以32位的float为例说明10.5的存储格式

规范化

转二进制

• (10.5_{(10)}=1010.1_{(2)})

转二为底的科学记数法形式

• (1010.1_{(2)}=1.0101_{(2)} imes2_{(10)}^{3_{(10)}})

• (3_{(10)})为指数

  • 为偏移前指数

• (1.0101_{(2)})为尾数

  • 必须保证尾数的第一位不是零，且小数点在第一位和第二位之间

    十进制第一位不是0可以是1-9，而二进制第一位不是零只能是1

性质符号填充

• 最高位填充符号，正填充0，负填充1
• 10.5是正数填充0

0
^
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

尾数转化填充

隐藏高位1和点

• (1.0101 o 0101)

  • 既然尾数第一位不能是0只能是1，大家都是1和点，也没有写的不要了都省略也行

低位补零

• (0101 o 0101 0000 0000 0000 0000 000)

  • 补齐23位

填充尾数

• 讲补齐后尾数填充在低23位上

0									0	1	0	1	0	0	0	0	0...	0	0	0
									^	^	^	^	^	^	^	^	^ all 0	^	^	^
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

指数转化填充

偏移前的指数加偏移量

• (3_{(10)}+127_{(10)}=130_{(10)})

  • 在32位单精度类型中，这个偏移量是127

    在64位双精度类型中，偏移量是1023

偏移后的指数转二进制

• (130_{(10)}=1000 0010_{(2)})

填充指数

• 讲补齐后尾数填充在性质符号位后的高8位上

0	1	0	0	0	0	0	1	0	0	1	0	1	0	0	0	0	0...	0	0	0
	^	^	^	^	^	^	^	^
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

0   1000 0010   0101 0000 0000 0000 0000 000

测试结果

• 测试网站
  • https://babbage.cs.qc.cuny.edu/IEEE-754.old/Decimal.html
  • https://www.h-schmidt.net/FloatConverter/IEEE754.html
  • https://float.exposed/

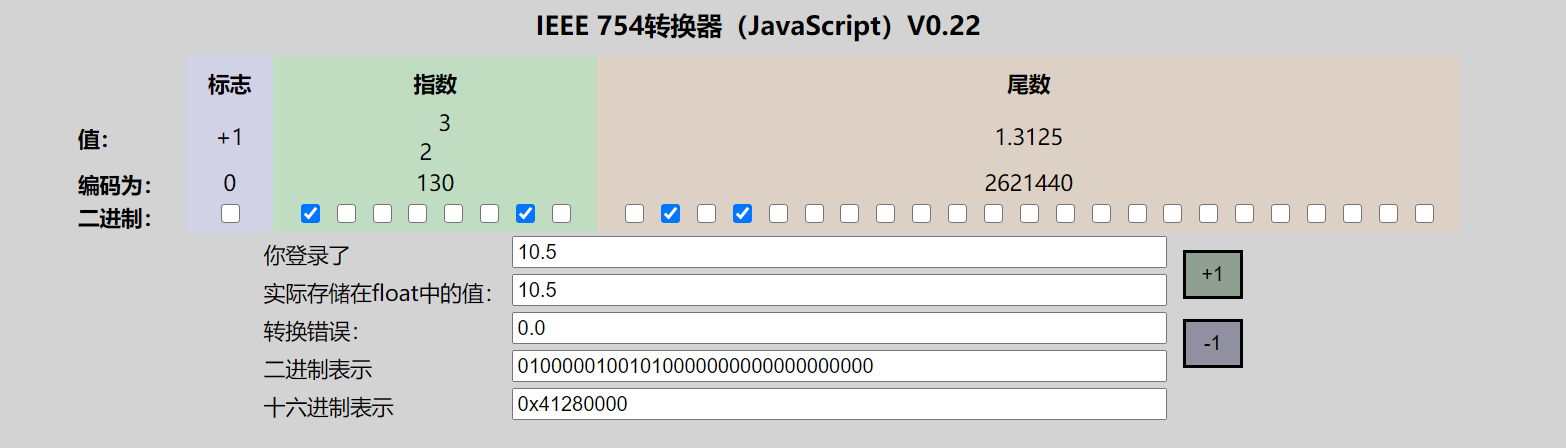
规格数读取(10.5为例子)

判断是不是规格数

• 除了符号位的高八位不全为0或者1，是规格数

• 为(sign 2^{exponent} imes fraction)形式

• 看其除了符号位的高八位是不是都是0是不是都是1

  • 如果不都是0且不都是1，则规格化的数
  • 如果都是0，则为非规格化的数
  • 如果都是1
    • 如果后面低23位全为0，则为无穷大
    • 如果后面低23位不全为0，则为NaN，not a number

0	1	0	0	0	0	0	1	0	0	1	0	1	0	0	0	0	0...	0	0	0
	^	^	^	^	^	^	^	^
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

0   1000 0010   0101 0000 0000 0000 0000 000

拆分符号位

• 符号位为0为正的,代入式子

• (sign 2^{exponent} imes fraction=+ 2^{exponent} imes fraction)

• 最高位为，符号位0是正的，1是负的

0	1	0	0	0	0	0	1	0	0	1	0	1	0	0	0	0	0...	0	0	0
^
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

拆分指数部分

读取指数部分

• 1000 0010

  • 除了符号位的高八位

0	1	0	0	0	0	0	1	0	0	1	0	1	0	0	0	0	0...	0	0	0
	^	^	^	^	^	^	^	^
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

指数部分转10进制偏移后指数

• (10000010_{(2)} o 130_{(10)})

减去偏移量转偏移前指数

• (130_{(10)}-127_{(10)}=3_{(10)})

代入式子

• (+ 2_{(10)}^{exponent} imes fraction=+ 2_{(10)}^{3_{(10)}} imes fraction)

拆分尾数部分

读取低23位

• 0101 0000 0000 0000 0000 000

0	1	0	0	0	0	0	1	0	0	1	0	1	0	0	0	0	0...	0	0	0
									^	^	^	^	^	^	^	^	^	^	^	^
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

去掉尾部0

• 0101 0000 0000 0000 0000 000 => 0101

补充高位1和点

• (0101_{(2)} o 1.0101_{(2)})

代入式子

• (+ 2_{(10)}^{3_{(10)}} imes 1.0101_{(2)})

转化成科学记数法或者普通形式

• (+ 2_{(10)}^{3_{(10)}} imes 1.0101_{(2)}=1010.1_{(2)})
• (1010.1_{(2)}=10.5_{(10)})

非规格数(二进制读取为例)

读取 0 0000 0000 0110 0000 0000 0000 0000 000 为例

0	0	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0...	0	0	0
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

判断是不是非规格数

• 除符号位为的高八位全部为0，是非规格数
• 也是(sign 2^{exponent} imes fraction)形式

0	0	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0...	0	0	0
	^	^	^	^	^	^	^	^
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

读取符号位

• 符号位为0，为正
• (+ 2^{exponent} imes fraction)

代入指数

• 非规格数指数固定为(1-127_{(10)}=-126_{(10)})

  • 非规格数指数是 1-偏移量 （而不是(0-127=-127)）

    这是规定

    规格数指数才是 实际指数-偏移量

• (+ 2_{(10)}^{-126_{(10)}} imes fraction)

读取代入尾数

读取尾数

• 0110 0000 0000 0000 0000 000

0	0	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0...	0	0	0
									^	^	^	^	^	^	^	^	^	^	^	^
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

去掉尾部0

• (0110 0000 0000 0000 0000 000_{(2)} o011_{(2)})

补充0.

• (0110_{(2)} o 0.011_{(2)})

  • 非规格数补充0.

    而规格数补充1.

代入式子

• (+ 2_{(10)}^{-126_{(10)}} imes fraction o + 2_{(10)}^{-126_{(10)}} imes 0.011_{(2)})

转化成普通形式

• (+ 2_{(10)}^{-126_{(10)}} imes 0.011_{(2)} o + 2_{(10)}^{-126_{(10)}} imes 0.375_{(10)} o 4.408103815583578155e-39)

注意用win10计算机算不出来，用手机计算机可以

测试结果

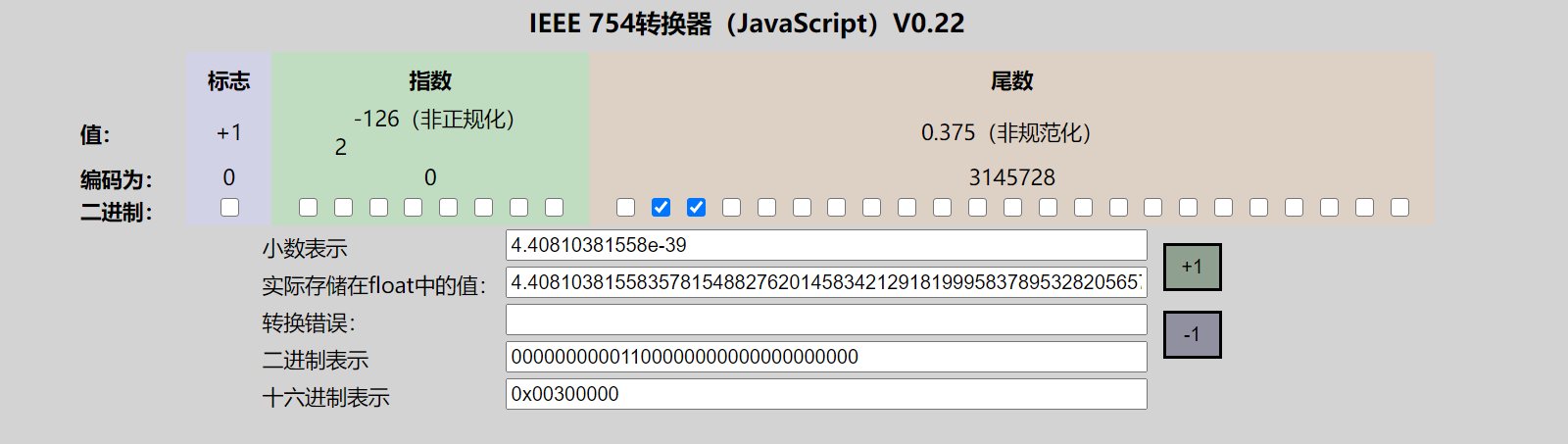
非规格数(写入是上面逆过程)

特殊数

• 最后一类数值是当指阶码（指数部分）全为1 的时候出现的。
• 当小数域全为0时， 得到的值表示无穷，
  • 当符号位为0时是正无穷 ,
  • 或者当符号位为1时是负无穷。
• 当我们把两个非常大的数相乘， 或者除以零时， 无穷能够表示溢出的结果。
• 当小数域为非零时， 结果值被称为"NaN", 即 “不是一个 数(Not a Number)" 的缩写。
  • 一些运箕的结果不能是实数或无穷， 就会返回这样的NaN 值，比如当计算(sqrt{-1})或(infty-infty)时。 在某些应用中，表示未初始化的数据时，它们也很有用处。
  • 这个不区分正负，都是NaN

无穷大

0	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0
正无穷	^ 都是1								^ 都是0
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

1	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0
负无穷	^ 都是1								^ 都是0
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

NaN

*	1	1	1	1	1	1	1	1	*	*	*	*	*	*	*	*	*	*	*	*
NaN	^ 都是1								^ *代表0或1都可以
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

范围与精度

IEEE754

32位float

范围

影响因素

• 主要由指数部分决定

0	1	0	0	0	0	0	1	0	0	1	0	1	0	0	0	0	0...	0	0	0
	^	^	^	^	^	^	^	^
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14~3	2	1	0
sign	exponent(8 bits)								fraction(23 bit)

#### 范围

下表中给出了重要的单精度存储格式位模式的示例。最大正正规数是以 IEEE 单精度格式表示的最大有限数。 最小正次正规数是以 IEEE 单精度格式表示的最小正数。最小正正规数通常称为下溢阈值。 （最大和最小正规数和次正规数的十进制值是近似的；对于所示的数字来说，它们是正确的。

公用名称	位模式（十六进制）	十进制值
+0	00000000	0.0
–0	80000000	–0.0
1	3f800000	1.0
2	40000000	2.0
最大正规数	7f7fffff	(3.40282347e+38)
最小正正规数	00800000	(1.17549435e–38=2^{-126})
最大次正规数	007fffff	(1.17549421e–38)
最小正次正规数	00000001	(1.40129846e–45)
+∞	7f800000	正无穷
–∞	ff800000	负无穷
非数字	7fc00000	NaN

NaN（Not a Number, 非数）可以用任何满足 NaN 定义的位模式表示。在上表中显示的 NaN 十六进制值只是可用于表示 NaN 的众多位模式之一。

---

	公用名称	位模式（十六进制）	十进制值	备注
	+∞	7f800000	正无穷
	NaN大于最大正规数且不为正无穷			由于存储表示非数字，就无法表示数
	最大正规数	7f7fffff	(3.40282347e+38)
eg	普通正的正规数	40000000	2.0	中间的数也不一是连续的，是离散的且涉及精度
	最小正正规数	00800000	(1.17549435e–38=2^{-126})
	最大次正规数	007fffff	(1.17549421e–38)
eg	普通的次正规数	0x00600000	(8.81620763117e-39)	非正规数有时候不归在float可表示的数里
	最小正次正规数	00000001	(1.40129846e–45)
err	小于最小次正规数且大于正0		无穷小的数	无法表示的数
	+0	00000000	0.0
	–0	80000000	–0.0
err	小于0且大于最大次负规数		无穷小的数	无法表示的数
	最大负次正规数	80000001	(-1.40129846e–45)
eg	普通的负次正规数	0x80600000	(-8.81620763117e-39)
	最大次负正规数	807fffff	(-1.17549421e–38)
	最大负正规数	80800000	(-1.17549435e–38=2^{-126})
eg	普通负的正规数	0xcc189680	(-40000000.0)
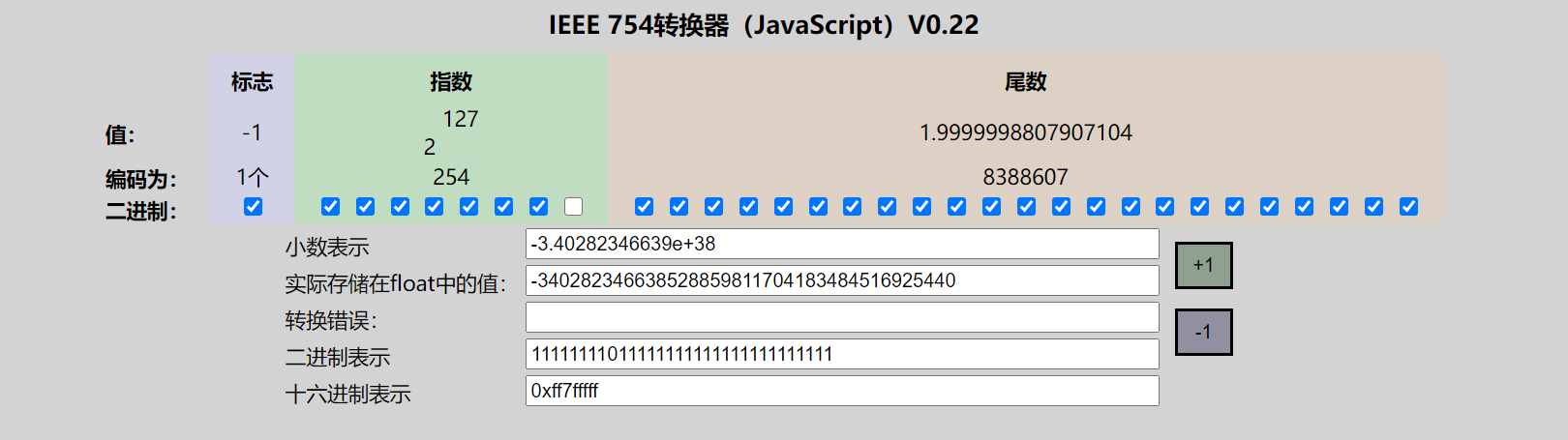
	最小负正规数	ff7fffff	(-3.40282347e+38)
	NaN小于最小正规数且不为负无穷	0x80189680	(-2.25804113503e-39)	无法表示的数
	–∞	ff800000	负无穷

• 规格数，（正的负的都是）最大

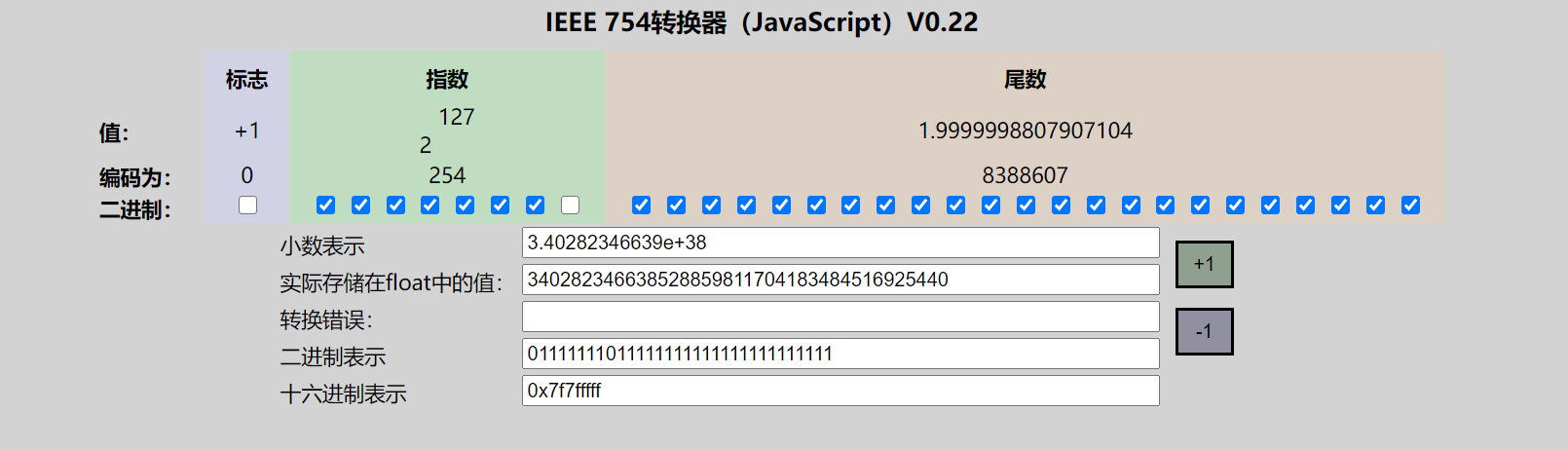
• 规格数，（正的）最小

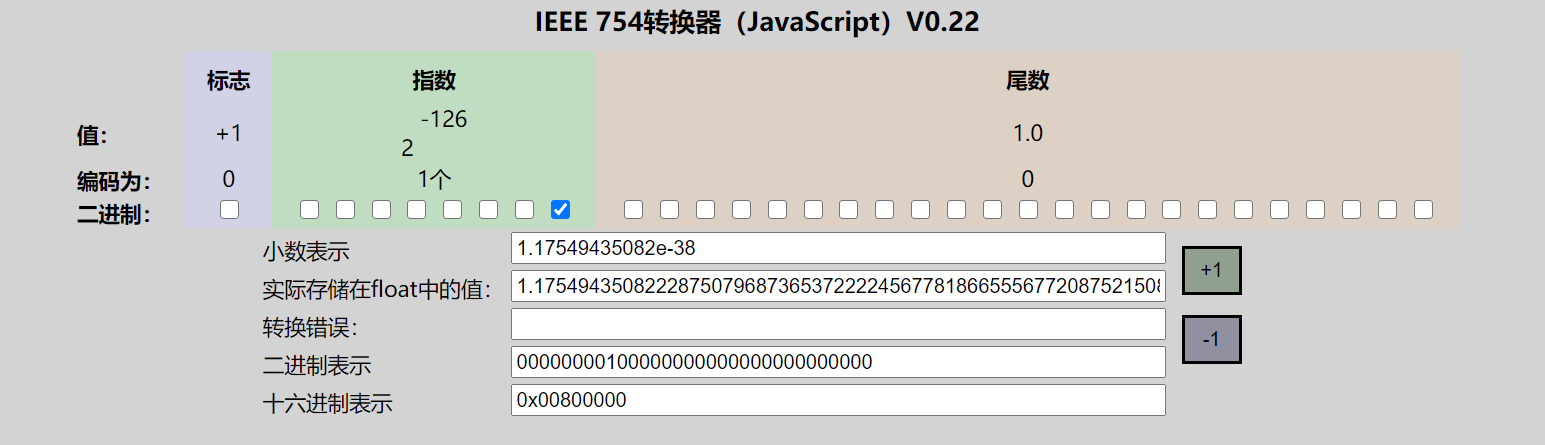
• 规格数，（负的）最大

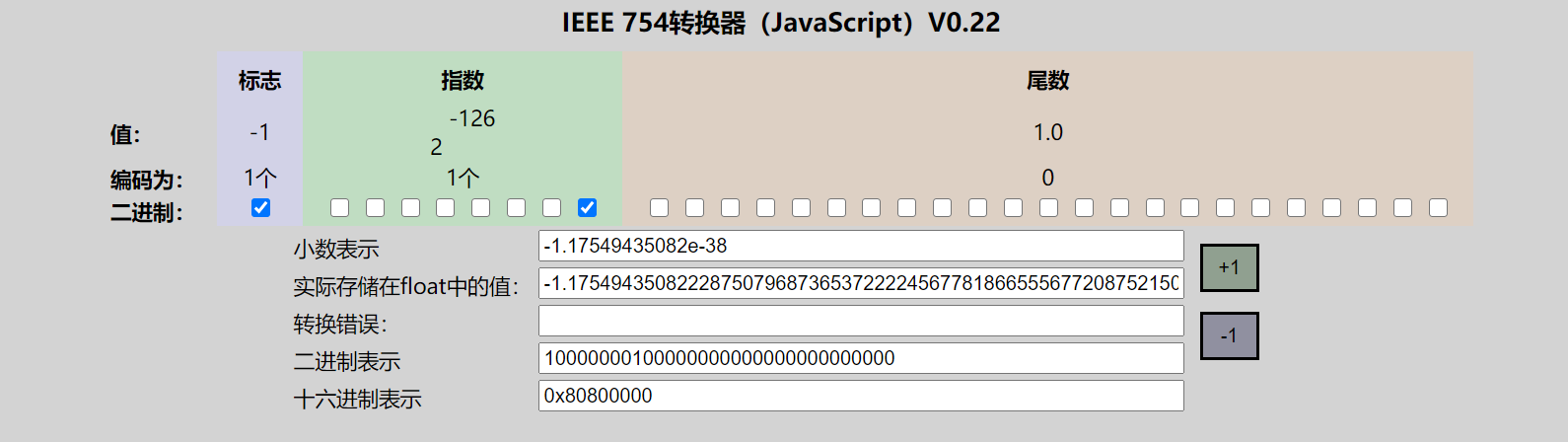
• 规格数，（正的负的都是）最小

• 次规格数，（正的负的都是）最大

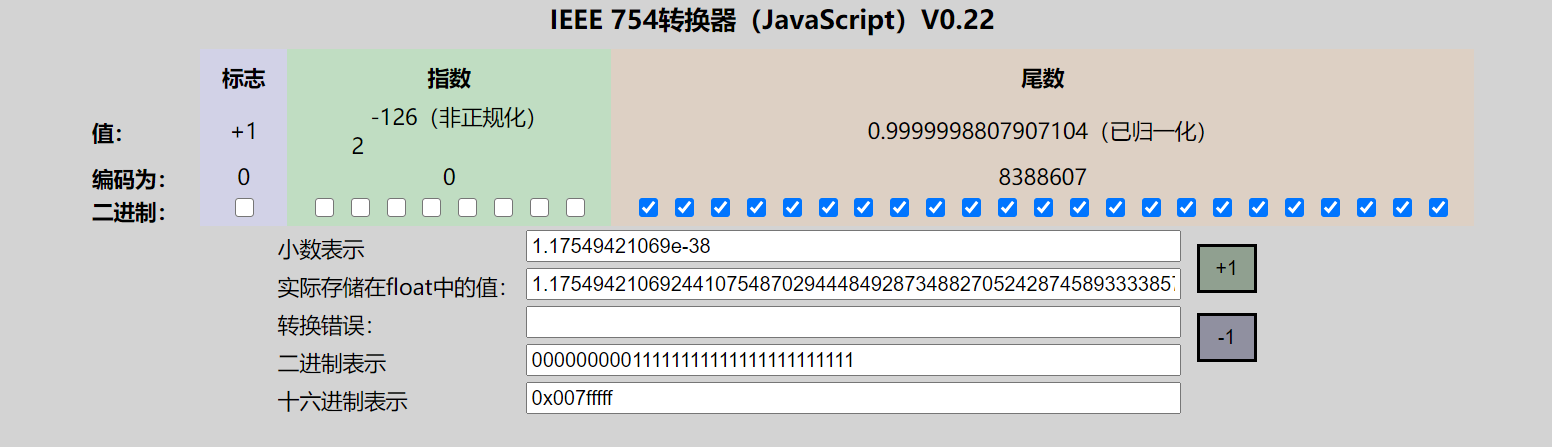
• 次规格数，（正的）最小

• 次规格数，（负的）最大

• 次规格数，（正的负的都是）最小

精度

• (2^{23}=8388608)

• 这么多组合，可以表示这么多不同的数,8388608这个一个7位数，6位是准的，7位不一定准

同理64位，有1符号位，11指数位，52尾数位

(2^{52}=4503 5996 2737 0496)是一个16位数，至少保证15位数存储是准的，至少可能存储15位有效数字

误差

• 十转二误差

  • 不是所有都可以表示为(sum_{i=1}^{n}[0|1] imes2^{N_i},(N_iin ext{整数},n eqinfty))

  • 如(0.000110011001……)存储时会截断存储产生误差

• 不能准确存储下列

  • 存储无穷大

  • 和无穷小量(包括 自然数+无穷小量 形式)，

  • 即有限的空间本身就是只能存储有限的离散的点

• 运算时产生无法准确存储的数据

参考

参考

• 兰德尔E.布莱恩特.深入理解计算机系统[M].龚奕利,贺莲,译.原书第3版.北京:机械工业出版社,2019
• https://docs.oracle.com/cd/E57201_01/html/E57330/z4000ac019178.html#scrolltoc
• https://ciechanow.ski/exposing-floating-point/
• https://people.eecs.berkeley.edu/~wkahan/ieee754status/754story.html
• https://zh.wikipedia.org/wiki/IEEE_754
• https://www.jianshu.com/p/8ee02e9bb57d
• https://www.jianshu.com/p/d71e4287ffa8

测试

• https://babbage.cs.qc.cuny.edu/IEEE-754.old/Decimal.html
• https://www.h-schmidt.net/FloatConverter/IEEE754.html
• https://float.exposed/

其他

• https://blog.csdn.net/u012611878/article/details/52455576
• https://www.cnblogs.com/lsgxeva/p/7614856.html
• https://www.jianshu.com/p/d71e4287ffa8