| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 2447 | Accepted: 678 | |
| Case Time Limit: 2000MS | ||
Description
There is an infinite square grid. Some vertices of the grid are black and other vertices are white.
A vertex V is called inner if it is both vertical-inner and horizontal-inner. A vertex V is called horizontal-inner if there are two such black vertices in the same row that V is located between them. A vertex V is called vertical-inner if there are two such black vertices in the same column that V is located between them.
On each step all white inner vertices became black while the other vertices preserve their colors. The process stops when all the inner vertices are black.
Write a program that calculates a number of black vertices after the process stops.
Input
The first line of the input file contains one integer number n (0 ≤ n ≤ 100 000) — number of black vertices at the beginning.
The following n lines contain two integer numbers each — the coordinates of different black vertices. The coordinates do not exceed 109 by their absolute values.
Output
Output the number of black vertices when the process stops. If the process does not stop, output -1.
Sample Input
4 0 2 2 0 -2 0 0 -2
Sample Output
5
Hint
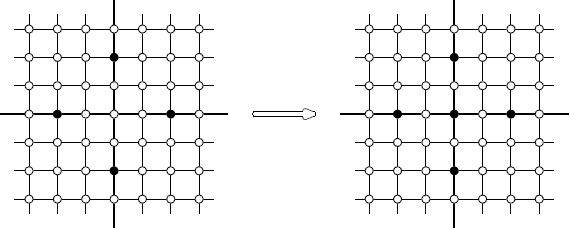
题意:无限大的棋盘上有黑白两种棋,前后左右都被黑棋包围的白棋都会最终变为黑棋,求最后有多少黑棋。
思路:因为棋盘是无限大的,所以要进行离散化,将有用的坐标节点取出来重新排列,譬如考虑横坐标的离散化,把所有黑子的横坐标取出,去掉重复,按原来的位置先后排序后再把横坐标赋予新的
值,即该横坐标从左到右排列排在第几位,以1开头;纵坐标也可以同理进行离散化。
离散化后所有被黑子包住的白子都将会变成黑子。此时的任务就是数出被包围的白子的个数。可以对离散化后的图形进行一行一行的扫描,白子的个数可以用树状数组进行存储,对于每一行的取出来的每一个黑子的
横坐标,先判断该横坐标在前面的行中有没有被取出过,如果取出过,那么这次取出意味着有上下两个黑子,之间也许夹着白子,那么可以通过树状数组把存储在该横坐标中的白子个数提取出来。树状数组在关于这个横坐标上
白子个数的记录清零,方便下一次记录新情况。之后从这个黑子的横坐标开始直到下一个黑子的横坐标为止,找出两者的坐标差(不含这两个横坐标本身),这个坐标差就是两个黑子之间白子的个数,之后就可以对中间这个
区间中的每一个横坐标在树状数组中对应位置处加1,表示这些横坐标上出现过一个白子并记录之。遍历所有行的所有黑子即可得到最终答案。
AC代码:
#define _CRT_SECURE_NO_DEPRECATE #include<iostream> #include<algorithm> #include<vector> using namespace std; typedef long long ll; const int N_MAX = 100000+4; int N; int X[N_MAX], Y[N_MAX]; vector<int>line[N_MAX];//一行一行的记录 bool visited[N_MAX]; ll bit0[N_MAX], bit1[N_MAX]; ll sum(ll *b,int i) { ll s = 0; while (i>0) { s += b[i]; i -= i&-i; } return s; } void add(ll *b,int i,ll x) { while (i <= N_MAX) { b[i] += x; i += i&-i; } } ll sum(int to) { return sum(bit1, to)*to + sum(bit0, to); } ll sum(ll*b,int from,int to) {//计算区间(from,to]的和 return sum( to) - sum( from); } void add(int from,int to,ll x) {//对[from,to]区间同时加上值x add(bit0,from,-x*(from-1)); add(bit1,from,x); add(bit0,to+1,x*to);//!! add(bit1,to+1,-x); } int compress(int *x) {//离散化,每一个x坐标的含义新定义为:所有的x坐标中排第几,1为下标起点 vector<int>v(N);//千万别忘记初始化,使用distance for (int i = 0; i < N;i++) { v[i] = x[i]; } sort(v.begin(), v.end()); v.erase(unique(v.begin(), v.end()), v.end()); for (int i = 0; i < N;i++) {//!!!!!!!1 x[i] = distance(v.begin(), lower_bound(v.begin(), v.end(), x[i])) + 1; } return v.size(); } int main() { scanf("%d",&N); for (int i = 0; i < N;i++) { scanf("%d%d",&X[i],&Y[i]); } int h = compress(Y); int w = compress(X); for (int i = 0; i < N; i++) {//离散化后,把坐标存起来,之后即可一行一行的考虑 line[Y[i]].push_back(X[i]); } ll res = N;//res记录最终的黑点数 for (int i = 1; i <= h;i++) {//!!!! vector<int>&xs = line[i];//对于每一行,查找黑点之间的白点个数 sort(xs.begin(),xs.end()); //!!!!!!!!!!!!!!! for (vector<int>::iterator it = xs.begin(); it != xs.end();it++) { int x = *it; ll s = sum(bit0, x - 1, x);//首先判断有没有以该值作为横坐标的白点,记录个数 if (visited[x]) {//如果这个横坐标以前到达过,再次到达就会封闭包围白点 res += s; } else visited[x] = true; add(bit0,x,-s);//在该横坐标处减去已经做记录的白点,清零,方便下次继续记录 //接下来计算从该黑点开始一直到下一个黑点为止中间的白点的个数 if ((it + 1) != xs.end()) { if(x+1<*(it+1)-1){//中间多于1个白点 add(x + 1, *(it + 1)-1, 1); } else if (x + 1 == *(it + 1) - 1) { add(bit0, x + 1, 1);//中间只有一个黑点 } } } } printf("%lld ",res); return 0; }