Viva Confetti
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 1025 | Accepted: 422 |
Description
Do you know confetti? They are small discs of colored paper, and people throw them around during parties or festivals. Since people throw lots of confetti, they may end up stacked one on another, so there may be hidden ones underneath.
A handful of various sized confetti have been dropped on a table. Given their positions and sizes, can you tell us how many of them you can see?
The following figure represents the disc configuration for the first sample input, where the bottom disc is still visible.
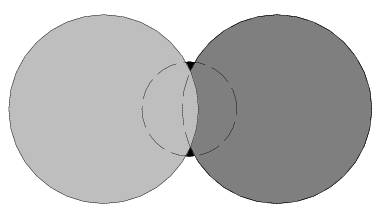
A handful of various sized confetti have been dropped on a table. Given their positions and sizes, can you tell us how many of them you can see?
The following figure represents the disc configuration for the first sample input, where the bottom disc is still visible.

Input
The input is composed of a number of configurations of the following form.
n
x1 y1 r1
x2 y2 r2
...
xn yn rn
The first line in a configuration is the number of discs in the configuration (a positive integer not more than 100), followed by one line descriptions of each disc : coordinates of its center and radius, expressed as real numbers in decimal notation, with up to 12 digits after the decimal point. The imprecision margin is +/- 5 x 10^(-13). That is, it is guaranteed that variations of less than +/- 5 x 10^(-13) on input values do not change which discs are visible. Coordinates of all points contained in discs are between -10 and 10.
Confetti are listed in their stacking order, x1 y1 r1 being the bottom one and xn yn rn the top one. You are observing from the top.
The end of the input is marked by a zero on a single line.
n
x1 y1 r1
x2 y2 r2
...
xn yn rn
The first line in a configuration is the number of discs in the configuration (a positive integer not more than 100), followed by one line descriptions of each disc : coordinates of its center and radius, expressed as real numbers in decimal notation, with up to 12 digits after the decimal point. The imprecision margin is +/- 5 x 10^(-13). That is, it is guaranteed that variations of less than +/- 5 x 10^(-13) on input values do not change which discs are visible. Coordinates of all points contained in discs are between -10 and 10.
Confetti are listed in their stacking order, x1 y1 r1 being the bottom one and xn yn rn the top one. You are observing from the top.
The end of the input is marked by a zero on a single line.
Output
For each configuration you should output the number of visible confetti on a single line.
Sample Input
3 0 0 0.5 -0.9 0 1.00000000001 0.9 0 1.00000000001 5 0 1 0.5 1 1 1.00000000001 0 2 1.00000000001 -1 1 1.00000000001 0 -0.00001 1.00000000001 5 0 1 0.5 1 1 1.00000000001 0 2 1.00000000001 -1 1 1.00000000001 0 0 1.00000000001 2 0 0 1.0000001 0 0 1 2 0 0 1 0.00000001 0 1 0
Sample Output
3 5 4 2 2
题意及思路:具体可以参考《算法竞赛入门经典 训练指南》P269的分析。
AC代码:
#define _CRT_SECURE_NO_DEPRECATE #include<iostream> #include<stdio.h> #include<algorithm> #include<queue> #include<set> #include<vector> #include<cstring> #include<string> #include<functional> #include<cmath> #include<stack> using namespace std; #define INF 0x3f3f3f3f #define pi acos(-1.0) double EPS = 4e-13; struct P { double x, y; P(double x=0,double y=0):x(x),y(y){} }; vector<P>ps; vector<double>r; int n; void clear() { ps.clear(); r.clear(); } //距离 double dist(const P&a,const P&b) { return sqrt((a.x - b.x)*(a.x - b.x)+(a.y - b.y)*(a.y - b.y));//!!!! } double normalize(double angel) { while (angel < 0.0)angel += 2 * pi; while (angel >= 2 * pi)angel -= 2 * pi; return angel; } int find_circle(P p,const vector<P>& ps,const vector<double>r ) {//返回覆盖点p的最上面的圆的编号 for (int i = r.size()- 1; i >= 0;i--) { if (dist(p, ps[i]) < r[i]) return i; } return -1; } void solve() { vector<bool>visible(n, false); for (int i = 0; i < n;i++) { vector<double>rads;//与其他圆相交的极角 rads.push_back(0.0); rads.push_back(2 * pi); for (int j = 0; j < n;j++) {//找到与圆i相交的所有交点 double a = r[i]; double c = r[j]; double b = dist(ps[i], ps[j]); if ( a + c < b ) // !!!!!!! continue; double theta = acos(double((a*a + b*b - c*c) /(2.0 * a*b))); double phi = atan2(ps[j].y-ps[i].y,ps[j].x-ps[i].x); rads.push_back(normalize(phi+theta)); rads.push_back(normalize(phi - theta)); } sort(rads.begin(), rads.end()); for (int j = 0; j + 1 < rads.size();j++) {//!!!!! double rad; rad = (rads[j] + rads[j + 1]) / 2.0; for (int k = -1; k <= 1;k+=2) {//该点向园内圆外分别稍微移一下 int t=find_circle(P(ps[i].x+cos(rad)*(r[i]+k*EPS),ps[i].y+sin(rad)*(r[i]+k*EPS)),ps,r); if (t != -1) visible[t] = true; } } } printf("%d ",count(visible.begin(),visible.end(),true)); } int main() { while (scanf("%d",&n)&&n) { for (int i = 0; i < n;i++) { double x, y, z; scanf("%lf%lf%lf",&x,&y,&z); ps.push_back(P(x, y)); r.push_back(z); } solve(); clear(); } return 0; }