题干
Input

Output

Example
Test 1: Test 2:
3 5
1 2 1 2
2 3 1 3
1 4
3 5
3 10
Tips

译成人话
给n个结点,n-1条无向边。即一棵树。我们需要给这n-1条边赋上0~ n-2不重复的值。mex(u,v)表示从结点u到结点v经过的边权值中没有出现的最小非负整数。计算下面等式的最大值:
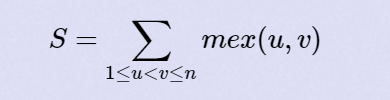
扯淡时间到:
看到题,头皮发麻,怎么想也想不出来,越是想越是觉得人是真的有极限的,于是,我不做人啦,老师!!
另外,我突然找到了一个很不错的视频题解???我大B站无所不有Σ(っ °Д °;)っ
咳~不玩梗了,关于这道题 ,我自己的确是没什么思路,所以,还是感谢郭军凯大佬和刘畅大佬的题解,给我这个小蒟蒻指了条明路 :D
首先,我们来看下面这张图:

我们一眼就能看到u1u2这条权值为0的边把这一堆节点分成了左右两堆,那么,根据定义我们能知道,无论是左还是右,只要是同一堆中的节点相互到达,答案一定是0,因为边肯定不经过0嘛,而0又肯定是最小的权。而如果左右两堆中的节点互相到达,那么一定要经过u1u2边也就是0权边,所以它的答案最小是1(不确定,因为我们不知道剩下的边权是多少,但最小一定是1,因为自然数中除了0就是1最小,更多的2,3,4…也是以此类推)
那么下一步,我们肯定是要一个个赋边权,那么怎么赋呢?下一步我们要赋值边权1,能考虑的边有u1v1,u1v2,v1v3,u2v4,u2v5…太多了。那么,我们再看一张图:

如图,我把v1v3这条边赋值为1,那么u1到v1,u1到v2,答案显然都是1,因为路径没经过1这条边,只有v1到v3答案为2,因为经过了1权边。
那么,我把u1v1这条边赋为1呢?

我们会发现,u1到v1,v1到v3,现在都经过了边权为1的边,此时答案都变成了2,显然比原来更大了。据此,我们可以推断,边权1赋给与0权边相邻的边时,答案最大,即最优。当赋边权2,边权3…时也是同理。
那么现在的问题是,与0权边相邻的边有u1v1,u1v2,u2v4,u2v5,这么多,我们该选哪个呢?

我们定义如图数组,在添加边权1之前,对于所有节点,只要路径经过u1u2即0权边,那么答案一定是1,对总答案贡献为siz[u1]*siz[u2];而路径不经过0权边的,跟一开始提到的一样答案都是0,对总答案没有贡献。所以此时在没加1权边时,除开u1u2外,总答案为 siz[u1]*siz[u2];

还是这张图,我们让它变得更一般化一点,u1u2表示为已确定权值的一条边,节点u1可表示为fa[v5][v1],节点u2表示为fa[v1][v5]。
我们的下一步加权选择有u1v1,u1v2,u2v4,u2v5,这里我只拿u1v1,u2v5两条边举例,别的边也是一样的道理,反正都会枚举到的。
如果我把下一个边权加在u1v1上,增大的答案就是1*siz[v1][v5]*siz[v5][v1](我们默认是按自然数从小到大顺序加权,每次权值都差1,故系数是1),再加上原来的dis[v1][fa[v1][v5]];
同理,把下一个边权加在u2v5上,增大的答案也是1*siz[v1][v5]*siz[v5][v1],再加上原来的dis[v5][fa[v5][v1]];
增大的答案都是一样的,所以我们最终比较的是dis[v1][fa[v1][v5]]和dis[v5][fa[v5][v1]]的大小,我们要取较大的那一个。
然后这题的思路就结束了,我们的步骤就是先预处理出siz[ ]和fa[ ][ ],再枚举i,j按公式找到dis[i][j]的最大值(这里要递归来找,因为我们不能保证枚举的顺序正好满足dis也是从小到大的顺序,中间会有空档,所以要递归)
最后的最后,开long long已经是常规操作了吧。
代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define ll long long
const int maxn=3005;
int head[maxn],len=0,n;
int root;
ll dis[maxn][maxn],fa[maxn][maxn],siz[maxn][maxn];
//dis[i][j]表示把从i到j间的m条边赋值0~m-1能得到的最大值
//fa[i][j]表示以i为根时,j的父节点
//siz[i][j]表示以i为根时,j节点的子树大小
struct Edge{
int next,to;
}edge[maxn<<1];
void Add(int u,int v){
edge[++len].next=head[u];
edge[len].to=v;
head[u]=len;
}
void Init(int u,int pa){//预处理fa[i][j]和siz[i][j]
siz[root][u]=1;//每节点的初始子树规模都是1,因为它自己就是一个节点
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(v==pa) continue;
fa[root][v]=u;//更新v的父节点
Init(v,u);//向子树方向递归
siz[root][u]+=siz[root][v];//更新子树规模:siz[父]+=siz[子]
}
}
long long Update(int u,int v){
if(u==v) return 0;//自己到自己肯定是0
if(dis[u][v]) return dis[u][v];//记忆化,减少重复计算
return (dis[u][v]=max(Update(u,fa[u][v]),Update(v,fa[v][u]))+siz[u][v]*siz[v][u]);//向下递归
}
int main(){
cin>>n;
int x,y;
for(int i=1;i<n;i++){
scanf("%d%d",&x,&y);
Add(x,y),Add(y,x);
}
for(int i=1;i<=n;i++){
root=i;
Init(i,-1);
}
ll ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
ans=max(Update(i,j),ans);//递归寻找答案的最大值
}
cout<<ans<<endl;
return 0;
}