开始学物理了!!!
先做两道题:
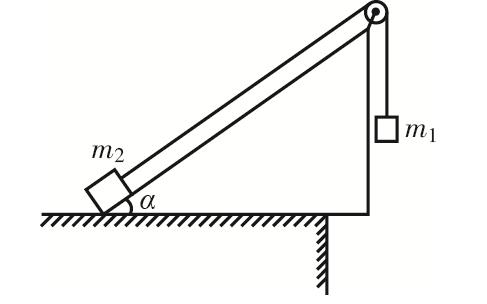
- 质量分别为m1和m2的两个小物块用轻绳连结,绳跨过位于倾角α = 30°的光滑斜面顶端的轻滑轮,滑轮与转轴之间的磨擦不计,斜面固定在水平桌面上,如图所示。第一次,m1悬空,m2放在斜面上,用t表示m2自斜面底端由静止开始运动至斜面顶端所需的时间。第二次,将m1和m2位置互换,使m2悬空,m1放在斜面上,发现m1自斜面底端由静止开始运动至斜面顶端所需的时间为t/3。求ml与m2之比。
一开始错写成
[frac {m_1g - frac{1}{2} m_2g} {m_2} cdot frac{t}{2}= frac {m_2g - frac{1}{2} m_1g}{3m_1} cdot frac{t}{6}
]
后来发现其实根本不是那样的,绳的拉力并不等于重力
【正解】
第一次物块运动的加速度a1分析如下:
对m2沿斜面方向受力分析,有
[T_1 − m+2gsinα = m_2a_1
]
由于有绳约束,m1的加速度也为a1,则对其竖直方向受力分析,有
[m_1g − T_1=m_1a_1
]
联立两式消去拉力T:可得
[a_1 = frac {m_1g − m_2gsinα }{ m_1 + m_2 } = frac { 2m_1 − m_2} { 2(m_1 + m_2)g }
]
[同理,第二次物块运动的加速度a_2
]
对m1沿斜面方向受力分析,有
[T_2 − m_1gsinα = m_1a_2
]
由于有绳约束,m2的加速度也为a2,则对其竖直方向受力分析,有
[m_2g−T_2 = m_2a_2
]
联立两式消去拉力T:可得
[a_2 = frac{ m_2g − m_1gsinα } { m_1+m_2} = frac { 2m_2−m_1 } { 2(m_1+m_2)g }
]
以l表示斜面的长度,则依题述有运动学关系
[l = frac {1} {2}a_1t^2= frac {1}{2} a_2( frac {t}{3} )^2
]
即得
[9a_1=a_2
]
,联立以上可解得
[frac {m_1}{m_2} = frac {11}{19}
]
- 一个密度均匀的圆柱,质量为m,半径为R,放在两个等高的台阶上,台阶一个固定不动,一个可无摩擦地滑动,如图所示.
当两支点的距离为2√R时,固定台阶对圆柱的支持力N,求此时可动台阶A的滑动速度.设所有摩擦均可忽略不计.
滑动的台阶和圆柱之间有速度关联.在圆柱静止系中,可动台阶上与圆柱的接触点只有切向速度.圆柱和静止的台阶有速度,加速度关联.即圆柱质心只有垂直于圆心到接触点的连线的速度分量,向心加速度为
[ frac {v_0^2} {R} $$.
圆柱法向受力提供向心加速度,可以得到圆柱质心的速度,再用关联可以得到可动台阶的速度.
由分析,圆柱的质心O相对于固定点C作圆周运动,以v0表示其速度大小,则有重力分量与支持力之差提供向心力
$$ mv_0^2R = mgcos45°−N, ]
所以解得
[v_0 = sqrt{ frac{ (sqrt{2}mg - 2N)R }{ 2m } }
]

由于BC=2√R,圆柱绕固定点C圆周运动,故轮缘B点的速度有:
[v_B = ω⋅sqrt{2}R = frac {v_0}{R}⋅sqrt{2} R=sqrt{2}v_0,v_B的方向垂直于BC向下.
]
[vB即为轮缘B点对地的速度vec{v}_{ B→G},vec{v}_{ A→B}必沿B点处圆弧切线方向,vec{v}_{ A→G}必沿水平方向,且此三者应满足vec{v}_{ A→G} = vec{v}_{ A→B} + vec{v}_{ B→C},
]
[即为图所示的关系,由图几何关系可见vec{v}_{ A→G} = vec{v}_{ B→G},即
]
[v = v_B = sqrt{2} v_0 = sqrt{ frac{ (sqrt{2}mg - 2N)R } { m } }
]
感觉物理白学了
From: 质心教育.