- 2D视图模型解析
- 3D视图模型解析
- 平移
- 旋转
- 伸缩
- 扭曲
- z轴方向平移与perspective的神秘关系
- matrix()终极变幻的方法
一、2D视图
2D视图就是默认平面上的每个点都与视线垂直,图形不会随视角变化发生视图变形。
二、3D视图
3D视图就是图形假设了一个视角和透视点,图形根据视角和透视点,展示图形在该视角和透视点的变形图形。

三、平移
- translate()
- translatex()
- translatey()
平移是基于2D视图的图像位置变幻,所以平移不会发生形变。相当于设置了设置定位(position+top/left),但是不会渲染引擎不会渲染平移元素不会放到独立的渲染层渲染,所以也就不会产生浮动流,且父级元素的overflow可以作用平移的子元素的溢出部分。
以上示例的关键代码:
1 /* 示例一 */ 2 /* 没有什么关键代码,就是两个普通的嵌套DIV */ 3 /* 示例二 : 基于示例一使用平移实现居中*/ 4 position:absolute;/* 父级设置了relative */ 5 left:calc(50%); 6 top:calc(50%); 7 transform:translate(-50%,-50%); 8 /* 示例三、四 使用平移溢出父级 overflow有效*/ 9 overflow:hidden;/示例四父级DIV/ 10 transform:translate(60px,60px);
需要注意的是translate()是用来设置纵横坐标同时偏移的方法,如果设置一个参数只有横向偏移。所以如果需求是一个方向的偏移建议使用translatex()或者translatey()。
四、旋转
- 2D旋转:rotate()
- 3D旋转:rotate3d()、rotatex()、totatey()
关于2D旋转和3D旋转需要注意的是,是web的平面图形基于2D空间和3D空间的旋转运动,2D空间的旋转就是在最前面介绍的2D视图模型的原理,在2D视图中旋转的是基于图形所在平面的某一点做绕该点的旋转运动。而3D空间的旋转是基于3D空间的绕空间上的某一条线旋转,假设视角固定(3D视图模型),由于图形的3D旋转产生视角移动,导致最终我们看到的web界面渲染的图形所出现的形变效果,这种效果就是transform的3D旋转效果。
需要注意的是web界面上的3D旋转模型是图形所在的平面做旋转运动,通常我们理解的日常三维空间的旋转是一个物体围绕另一个物体运动,运动的物体参照的是另一个物体的三维空间坐标进行运动,但是在web界面中的3D旋转是基于图形所在平面自己的三维坐标进行旋转,由旋转的图形在三维空间发生位移而图形所在的平面同步偏转位移,所以web中的3D旋转所基于的三维坐标会同步跟着图形移动。
简单的说,就是3D旋转时坐标轴会跟着图形旋转而旋转,所以在做连续旋转运动时需要注意所参照的坐标发生的位移问题。
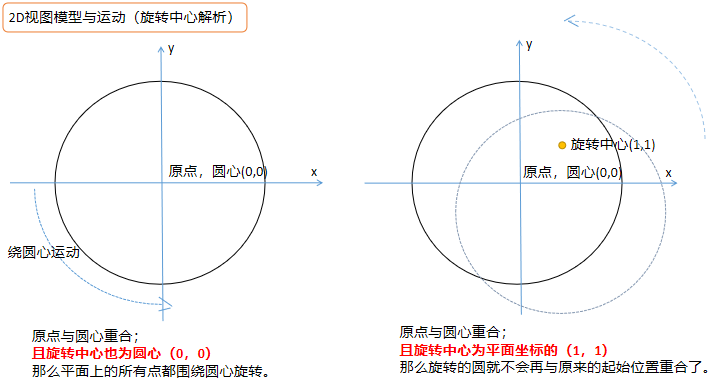
关于2D旋转,重点在于旋转中心的设置(transform-origin),默认的旋转中心是在元素的中心,也就是示例二、三所表现的样式。transform-origin(a,b)需要两个参数,分别是横向位置、纵向位置;
- 横向坐标值:length(距离元素最左侧的距离,可以超出元素的宽度)、百分比(基于元素宽度计算)、left(横向坐标在左侧,同length等于0)、right(元素的最右侧,同length等于宽度)。
- 纵向坐标的值:length、百分比、top、bottom。
示例中的关键代码:
1 /*示例一省略*/ 2 /*示例二*/ 3 transform:rodate(45deg); 4 transform-origin:50% 50%;/*默认值同等与center center*/ 5 /*示例三*/ 6 @keyframes run{ 7 0%{transform:rodate(0deg)} 8 100%{transform:rodate(360deg)} 9 } 10 animation:run 20s cubic-bezier(0,0,1,1) infinite; 11 /*示例四*/ 12 @keyframes run1{ 13 0%{transform:rodate(30deg)} 14 100%{transform:rodate(60deg)} 15 } 16 left:50%; 17 transform-origin:0px 0px: 18 transform:rotate(30deg); 19 animation:run1 1.5s cubic-bezier(0,0,1,1) infinite alternate;
虽然2D视图的旋转效果比较简单,但是重点并不在于应用2D视图,首先我们需要通过2D旋转来了解一个web视图基础知识,就是坐标原点和坐标方向。虽然在上面的四个示例中不能直接看到这其中的规律,但是还是可以推断出在web中的坐标方向y轴与我们通常的数学物理中的坐标轴方向不一致,在web视图中的y轴方向是指向下方的。

关于设置旋转中心transform-origin我们只能设置x轴和y轴的坐标,z轴默认始终是0。z轴更关键的是在于设置3D变换的视距,如果不设置3D视觉的话,图形发生的3D旋转在web界面上表现的视图是由2D视图模型看到的图形因为旋转发生宽高伸缩变换,并非3D视图变换,具体有什么区别通过以下几个示例来了解。
以上四个示例用来比较解析2D视图扭曲3D旋转与3D视图的3D旋转的区别,另外又通过示例三、四对比出视距对3D视图展示的影响。首先需要了解几个重要的CSS3属性:
- transform:rotateY();/*3D旋转中心轴*/
- transform-origin:length length;/*2D旋转中已经解析过*/
- perspective:length;透视距离
- transform-style:preserve-3d/flat;/*设置图形位于3维空间(3D视图)还是图形所在平面的扁平化处理(2D视图扭曲的3D旋转)*/
再来看示例中的关键代码:
1 /*示例一省略*/ 2 /*示例二*/ 3 transform:rotateY(45deg);/*以Y轴为旋转轴,顺时针转45°*/ 4 transform-origin:50% 50%;/*默认值*/ 5 /*示例三*/ 6 perspective:100px;/*默认视线在z轴方向上距离旋转中心的距离-设置在父级元素上*/ 7 transform-style: preserve-3d; 8 transform-origin:50% 50%;/*默认旋转中心*/ 9 transform:rotateY(45deg); 10 /*示例四:相对示例三只有视距发生变化*/ 11 perspective:300px;
这里有一个有意思的地方,或者说需要注意的地方,当使用transform:rotateX/rotateY/rotate3d时,必须要设置视距perspective的实现距离,这个属性不能设置0像素或者是负像素值,只有设置了perspective大于0像素的视距3D旋转视图才会有效,不然展示出来的视图就是2D视图下的3D旋转扭曲图形(如示例二)。
然而,我测试transform-style时,不论设置三维空间与否,如果不设置perspective的视距都不会有任何变化,但是如果设置了perspective的视距但不设置transform-style会正常出现3D视图,也就是说我测试的结果是transform-style实质上没有任何意义,是否有三维空间视图取决于perspective的控制,这个地方我暂时没有找到合理的解释,如果有知道的朋友还请不吝指教。
关键代码:
1 /*示例二*/ 2 transform:rotateY(45deg); 3 /*示例三*/ 4 transform:rotateY(45deg) rotateX(45deg); 5 /*示例四*/ 6 transform:rotateY(45deg) rotateX(45deg) rotateZ(45deg); 7 /*示例五*/ 8 transform: rotate3d(0, 10, 0, 45deg) rotate3d(10, 0, 0, 45deg) rotate3d(0, 0, 10, 45deg);
图解旋转与坐标的关系:
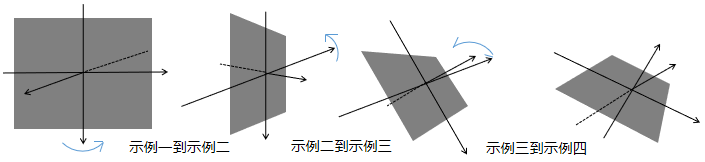
由代码示例展示到图解分析,还记得我在旋转部分开始文字解析的时候就说过的,3D旋转变换时实质上是图形所在平面绕旋转轴旋转,坐标永远都会跟随平面的旋转而旋转。
最后还是提一下关于rotate3d()这个函数吧,这个函数可以实现自定义旋转轴,如果只在一个坐标轴方向设置参数就表示以该坐标轴为旋转中心,参数大小无关(只要不等于0);如果设置多个坐标方向的参数,就会以设定的坐标参数大小来计算出自定义的旋转轴,这需要一些几何知识,三维空间的物理知识或许更准确,这些都不重要,重要的是你还记得这些高中时的知识。
五、伸缩变换、与对平移的影响
- scale()
- scalex()
- scaley()
- scalez()
- scale3d()
关于伸缩变换方法需要注意的就是元素视图伸缩后,在当前作用视图的平面上保留伸缩状态,如果图形发生其他视图变换,变换后的图形视图会因为之前的平面伸缩发生伸缩变换。这种影响主要可以从两种情况来理解,比如图形视图在x轴方向发生伸长2倍操作,接着触发x轴方向的平移,这时候平移的实际距离是设定参数的2倍;第二种情况就是当视图还是x轴发生2倍伸长,然后接着元素图形发生2D变换旋转90°,这时候旋转后的图形Y轴就与之前的X轴平行了,所以旋转后的图形Y轴方向会作用之前视图X轴的2倍伸长。用下面的两个示例来理解。
在展示示例之前还需要注意的是,元素图形伸缩是基于变换中向四周伸缩的,所以默认的变换中心在元素的中心点上,图形就会基于中心点向四周拉伸。
1.下面来展示第一种情况,伸缩变换scale()对平移translate()产生的影响:
实现效果的关键代码:
1 /*示例一没有任何变换属性的100*100的div*/ 2 /*示例二 宽高100px 变换中心设置为0px 0px(左上角),横向伸长一倍,平移100px*/ 3 transform-origin:0px 0px; 4 transform:scale(2,1) translateX(100px);
2.伸缩变换对旋转后的图形的影响:
这个示例我将富文本内编辑的示例代码全部贴出来对比(规律在前面已经解析过了,就不重复了):
1 <div style=" 100px; height: 100px; background-image: linear-gradient(to left,#CD853F, #CD69C9);"> </div> 2 <div style=" 100px; height: 100px; background-image: linear-gradient(to left,#CD853F, #CD69C9); transform-origin: 100px 100px; transform: scale(2,1); margin-left: 100px; margin-top: 10px;"> </div> 3 <div style=" 100px; height: 100px; background-image: linear-gradient(to left,#CD853F, #CD69C9); transform-origin: 100px 100px; transform: scale(2,1) rotate(90deg); margin-left: 100px; margin-top: 10px;"> </div>
最后关于变换伸缩,我在解析中使用的是视图平面拉伸,也有说成是视图的坐标拉伸,其描述的都是元素图形所在平面的伸缩变换。
然后关于关于scalez()或者scale3d()是z轴方向的拉伸,但由于web视图是2D图形,没有厚度,所以在2D试图变换中不会产生变化,但是在3D旋转视图变化中就会产生作用了。变化规律依然不变。
六、扭曲变换与坐标的关系及对其他变换的影响
- skew()
- skewx()
- skewy()
横向扭曲相当于拉伸x轴方向上的两条边向两边移位,导致y轴倾斜并被拉伸,反之纵向扭曲相当于y轴方向上的两条边向两边移位,导致x轴倾斜被拉伸。先来看图解:

所以被横向扭曲的图形如果在发生y轴方向的平移就是一个倾斜的平移,同理基于y轴的旋转也会是一个倾斜的旋转。
接着来看一个skew()在纵横两个方向上同时出现扭曲的变换:
关键代码:
1 @keyframes skew3{ 2 0%{transform:skew(0deg, 0deg)} 3 25%{transform:skew(45deg, 45deg)} 4 50%{transform:skew(0deg ,0deg)} 5 75%{transform:skew(-45deg ,-45deg)} 6 100%{transform:skew(0deg ,0deg)} 7 } 8 animation: skew3 5s cubic-bezier(0,0,1,1) infinite;
这种扭曲变形所产生的空间感是由视觉的错觉产生的,并非采用3D视图。
七、z轴方向平移与perspective的神秘关系
7.1在第三部分内容解析了关于2D平移的变换,在2D变换中,视图不会出现形变,只产生位置变化。但是在Z轴方向上的平移变换就是由视距perspective共同产生作用,正常情况下我们所理解的视距与视图的变换都是近大远小,但是在屏幕视图中,我们所看到的图像是模拟三维空间中图像在屏幕上的投影。所以在不设定Z轴平移transform:translateZ()时就默认图形与屏幕所在的平面重合,在这种情况下移动视距perspective屏幕中的图像不会发生任何变化。因为屏幕不会随视线距离产生变化。
如果translateZ()的参数大于0时,就相当于图形遮挡在屏幕前面,所以视距越接近图形,图形在屏幕上的投影就会越大,如果视线与屏幕的距离小于图形在Z轴中上的正向移动距离,图形就会消失。
如果translateZ()参数小于0时,就相当于图形在屏幕的后方,屏幕上所呈现的视图只是视线与图形的视角的一个切面,这时候会因为视距越近,视角越小,导致图形在屏幕上的切面越小。简单地说就是图形translateZ()的参数小于0时,视距越小,视图越小。

关键代码:
1 @keyframes pers{ 2 0%{perspective:1000px;} 3 100%{perspective:100px;} 4 } 5 /*父级元素*/ 6 perspective:1000px; 7 animation:pers 5s cubic-bezier(0,0,1,1) infinite; 8 /*示例一默认*/ 9 /*示例二*/ 10 transform:translateZ(60px); 11 /*示例三*/ 12 transform:translateZ(-60px);
7.2原来transform-style是这么用的:
当两个DIV嵌套,并设置子元素在Z轴上向正方向平移一段距离,然后旋转父级DIV,从3D视图的逻辑上来说这时候可以看到父子元素之间会出现Z轴上的距离,但是由于默认的浏览器渲染模式下旋转的元素和其子元素是保持在一个平面上渲染的,所以默认情况下只能看到子元素的旋转效果。在这种情况下CSS3提供了transform-style属性来改变元素内部的空间渲染模式,但设置transform-style: preserve-3d时就可以出现父子元素保持了Z轴方向上的空间距离,在旋转上就可以同时看到父子元素了。
1 <div style=" 100%; display: flex; flex-wrap: wrap; perspective: 800px; justify-content: center; align-items: center;"> 2 <div style="widht: 100px; height: 100px; background-color: red; transform: rotateY(25deg);"> 3 <div style=" 100px; height: 100px; background-color: blue; transform: translateZ(100px);"> </div> 4 </div> 5 <div style="widht: 100px; height: 100px; margin-left: 50px; background-color: red; transform: rotateY(25deg); transform-style: preserve-3d;"> 6 <div style=" 100px; height: 100px; background-color: blue; transform: translateZ(100px);"> </div> 7 </div> 8 </div>
7.3原来transform-origin可以定义3维旋转中心!!!
这里展示的是一个2维视图效果,3维视图效果见代码,关键的一行代码在这里:transform-origin: 100px 0px -500px;

1 <style> 2 *{ 3 margin: 0; 4 padding: 0; 5 } 6 :root 7 ,body{ 8 height: 100%; 9 perspective: 800px; 10 } 11 @keyframes origin3w{ 12 0%{ 13 transform: rotateY(0deg) ; 14 } 15 50%{ 16 transform: rotateY(180deg) ; 17 } 18 100%{ 19 transform: rotateY(360deg) ; 20 } 21 } 22 div{ 23 position: absolute; 24 top: calc(50% - 50px); 25 left: calc(50% - 50px); 26 width: 100px; 27 height: 100px; 28 background-size: cover; 29 transform-origin: 100px 0px -500px; 30 border-radius: 50px; 31 background-color: red; 32 animation: origin 10s cubic-bezier(0,0,1,1) infinite; 33 } 34 </style> 35 <div ></div>
八、matrix()终极变幻的方法
了解matrix()函数之前,必须先了解以下矩阵,在matrix()中只应用到了乘法矩阵,所以接下来也只针对乘法矩阵加以说明。矩阵在数学中的定义就是一个用来排列复数和实数的集合,在这里我们暂时不必要去研究复数和实数这些数学理论,我们只需要知道矩阵在matrix()中的应用就相当于一个用来存储数据的数据单元,那它怎么存储数据呢?先来看一些例子:
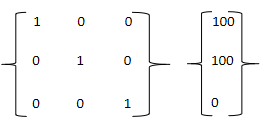
上面的示例中就是两个矩阵,第一个矩阵叫做三行三列矩阵,第二个矩阵叫做三行一列矩阵。接着来看什么是乘法矩阵(为了更好的表达乘法矩阵采用字母替代数值来表示):
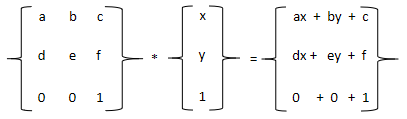
相信你已经发现规律了,所谓的乘法矩阵就是第一个矩阵的横向数据乘以对应的第二个纵向数据的和就得到了一个新的矩阵。如果第二个矩阵是两列的话,计算得到的矩阵就是两列的矩阵。来看下面这个示例:

在矩阵中的表示方法不存在逗号,这里为了更好的展示和理解我添加上了逗号,这个不是重点,重点是在matrix()中的第二个矩阵只需要一列就够了,不会出现上面这个相对复杂一些的矩阵。那再matrix()中需要怎么样的矩阵呢?又是怎么应用的呢?下面来看一组乘法矩阵转化成matrix()的计算逻辑和transform变换的应用:
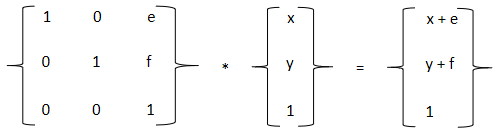
看到这个乘法矩阵是不想到了什么?先不要看第一个矩阵,看后面两个,第二个矩阵的x和y可以用来表示在平面上的一个点的坐标。假设x和y表示了某个图形的一个像素点,那么e就表示这个像素点在x轴方向的平移距离,f就表示这个点在y轴方向上的平移距离。
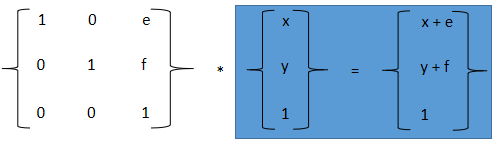
x和y是我们已知的图形的,e和f就是我们要对图形变换在平面内进行平移操作的横向和纵向的距离。再回头来看第一个矩阵,这就是我们需要在matrix的参数。
transform:matrix(1,0,0,1,e,f); ===>同等与transform:translate(epx,fpx);

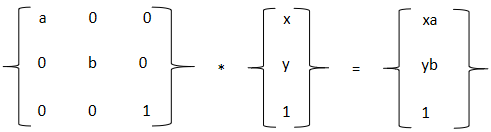
matrix()的取值就是在第一组矩阵中的上面两行获取的,至于为什么会有第三行,后面你就知道了,在平面变换中暂时只需要前面两行。通过上面的示例我们推导出matrix实现transform的平移公式。接着来看伸缩是不是就很简单了,transform:matrix(a,0,0,b,0,0); ===>同等与transform:scale(a,b);
然后来个有点梦幻的:
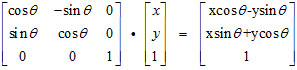
别飘,这是rotate()的乘法矩阵,实在是不敢吹牛了,给个链接大家自己看着办吧https://www.cnblogs.com/Ivy-s/p/6786622.html。
但是我依然没有有关于z轴的变换矩阵解析,这种梦幻的东西还是留给数学高手来解决吧。凌晨两点半了,睡觉。
