其实题目暗示了算期望,有两个难点。第一点要想到算每个site的期望;第二个是怎么算期望。
其实我一开始也想到了考虑每个site对于答案的贡献,但考虑到每个site对答案的贡献与上一个rest site在哪有关所以没有想出来。这就是第二个难点,我们引入概率来解决每个点的期望。
第n个site的期望是
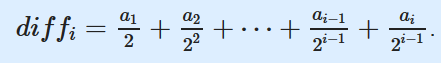
这个点之前就有rest site的概率是1//2,上两个才有rest site的概率是1/4,以此类推。得到这个公式后优化维护一个last代表上一个site的期望,就O(N)做完了。
1 #include<iostream> 2 using namespace std; 3 4 int n,a[1000005];//mi[i]为 2^i % mod 的值 5 long long ans,last,mi[1000005]; 6 int mod = 998244353; 7 8 int main(){ 9 cin>>n; 10 for(int i=1;i<=n;i++) scanf("%d",a+i); 11 12 mi[0]=1; 13 for(int i=1;i<=n;i++) mi[i]=(mi[i-1]*2)%mod; 14 15 for(int i=2;i<=n;i++){ 16 ans = (ans + (last + (mi[n-i]*a[i-1])%mod)%mod)%mod; 17 last = (last + (mi[n-i]*a[i-1])%mod)%mod; 18 } 19 20 for(int i=1;i<=n;i++) ans = (ans + (mi[n-i]*a[i])%mod)%mod; 21 cout<<ans; 22 23 return 0; 24 }