1.现代计算机存储和处理的信息都以二值信号表示。
2.机器为什么要使用二进制进行存储和处理?
答:二值信号能够很容易的被表示、存储、传输。例如:
可以表示为穿孔卡片上有洞和无洞、导线上的高压和低压,顺逆时针的磁场。
3.大多数机器使用8位的块或者byte(字节),作为最小可寻址的内存单位,而不是访问内存中的单独位。
4.机器级程序将内存视为一个非常大的字节数组,称为虚拟内存。
内存的每个字节都由唯一的数字来标识,称它为地址。
所有的地址集合就称为虚拟地址空间。
5.根据机器的不同,我们可以将存储顺序分为大端法和小端法。
大端法:字节值从小到大的排序。
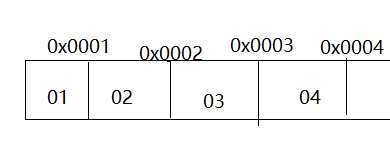
小端法:字节值从大到小的排序。
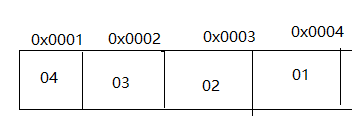
大多数的inter兼容机都只用小端模式;
IBM和Oracle大多数机器按大端模式操作;
安卓和IOS都只能运行小端模式。
一旦选择特定的操作系统,那么字节的顺序就固定下来了。
PS:至今也没确定统一的字节顺序,所以可以根据存储的数据不同,选择相应机器,可提高性能,也可以买双端法的处理器。
下面使用代码测试不同系统的端显示:
环境:windwos10 64位 处理器:Inter I7-7500U
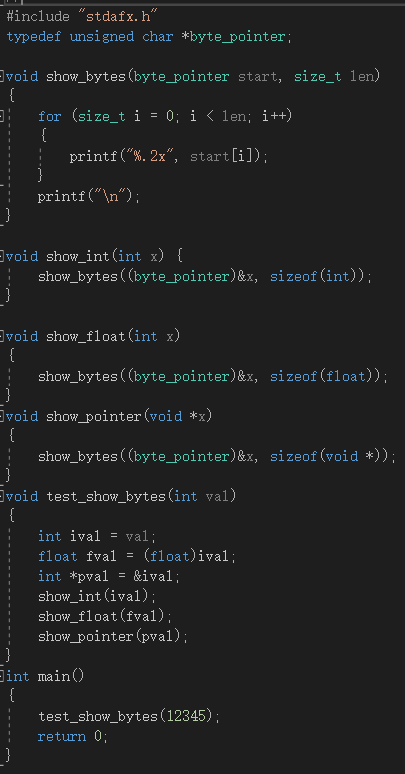
运行结果:

结果:int和float的结果是一样的,指针值和机器相关。
值12345的int十六进制表示为0x00003039.
可以看出在windows系统上最低的字节值0x39最先输出,所以windows使用的小端法。
其他小端法系统为Linux32,linux64。
在sun为大端法机器。
6.不同的机器类型使用不同的且不兼容的指令和编码方式;
即使是完全一样的进程,运行在不用系统上也会有不同编码规则,因此二进制代码是不兼容的。
二进制代码很少能在不同机器和操作系统组合之间移植。
7.确定一个位级表达式的结果的最好方法就是将十六进制参数扩展了二进制表示并执行二进制运算,然后转回十六进制。
8.补码,位运算。
根据补码转换无符号数公式:
x+2w x<0
T2Uw(x)=
x, x≥0
x T2U4(x)
-8 8
-3 13
5 5
12|-5 =》11110100 | 11111011 =11111111 输出结果为-1
开头符号位为1,其余各位取反,然后再整个数加1。 所以 11111111的补码是10000000 符号位为1, 所以得出10000001(-1)
还有无符号转换为补码等公式不一一列举了,具体请看该书。
其他:
(摘自其他博主 https://www.cnblogs.com/tjudzj/p/4190878.html)
补码:
(1)正数的补码:与原码相同(已知原码求补码)
例如:+9的原码是0000 1001。补码也是0000 1001。
(2)负数的补码:符号位为1,其余位为该数绝对值的原码按位取反,然后整个数加1。
例如:-7原码为1000 0111(高位为符号位,1表示负数,0表示正数),补码为1111 1001.
位运算:
(1)正数右移位(以85为例,可以视作int 、long、uint、ulong之一,按哪个规则都行)
85的二进制表示: 0000 0000 0000 0000 0000 0000 0101 0101
85右移(>>)3位: 0000 0000 0000 0000 0000 0000 0000 1010
移位后的结果十进制表示: 10
(2)负数右移位(以-85为例,可以视作int 、long之一,此处视为int,32位)
-85的二进制补码表示: 1111 1111 1111 1111 1111 1111 1010 1011
-85左移(>>)3位: 1111 1111 1111 1111 1111 1111 1111 0101
移位后结果的原码表示: 1000 0000 0000 0000 0000 0010 0000 1011
移位后的结果十进制表示: -11
最后,第二章习题太多,具体请看该书并实现。