SPFA是Bellman-Ford算法的一种队列实现,减少了不必要的冗余计算。
主要思想是:
初始时将起点加入队列。每次从队列中取出一个元素,并对所有与它相邻的点进行修改,若某个相邻的点修改成功,则将其入队。直到队列为空时算法结束。
这个算法简单的说就是队列优化的bellman-ford,利用了每个点不会更新次数太多的特点发明的此算法,所以它也是可以处理负边的。
SPFA在形式上和广度优先搜索(BFS)非常相似,不同的是BFS中一个点出了队列就不可能重新进入队列,但是SPFA中一个点可能在出队列之后再次被放入队列,也就是说一个点修改过其他的点之后,过了一段时间可能会获得更短的路径,于是再次用来修改其他的点,这样反复进行下去。
时间复杂度是O(kE),E是边数,K是常数,平均值为2。
算法实现:
dis[i]记录从起点s到i的最短路径,w[i][j]记录链接i、j边的长度,pre[v]记录前趋。
team[1……n]为队列,头指针head,尾指针tail。
布尔数组exist[1……n]记录一个点是否现在存在在队列中。
初始化:dis[s]=0,dis[v]=∞(v≠s),memset(exist,false,sizeof(exist));
起点入队:team[1]=s;head=0;tail=1;exist[s]=true;
do
{
1.头指针向下移一位,取出指向的点u。
2.exist[u]=false;已被取出了队列。
3.for与u相连的所有点v //注意不要去枚举所有点,用数组模拟邻接表储存
if( dis [ v ] > dis[ u ] + w [ u ][ v ])
{
dis [ v ] = dis [ u ] + w [ u ][ v ];
pre [ v ] = u;
if ( != exist [ v ])
{
尾指针下移一位,v入队;
exist [ v ] = true;
}
}
}
while( head < tail );
循环队列:
采用循环队列能够降低队列大小,队列长度只需开到2*n+5即可。
以上就是标程,根据我个人理解,下面是算法的实现过程:
先给一道题:
【题意】
给出一个图,起始点是1,结束点是N,边是双向的。求点1到点N的最短距离。哈哈,这就是标准的最短路径问题。
【输入格式】
第一行为两个整数N(1≤N≤10000)和M(0≤M≤200000)。N表示图中点的数目,M表示图中边的数目。
下来M行,每行三个整数x,y,c表示点x到点y之间存在一条边长度为c。(x≠y,1≤c≤10000)
【输出格式】
输出一行,一个整数,即为点1到点N的最短距离。
如果点1和点N不联通则输出-1。
【样例1输入】
2 1
1 2 3
【样例1输出】
3
【样例2输入】
3 3
1 2 5
2 3 5
3 1 2
【样例2输出】
2
【样例3输入】
6 9
1 2 7
1 3 9
1 5 14
2 3 10
2 4 15
3 4 11
3 5 2
4 6 6
5 6 9
【样例3输出】
20
我们先来举个例子,一个连通图中共有6个点,每两个点之间有连线(有向、无向都行,这里采用的是无向),边权都已给出,求从1号点到6号点的最短路径长度。
如图:
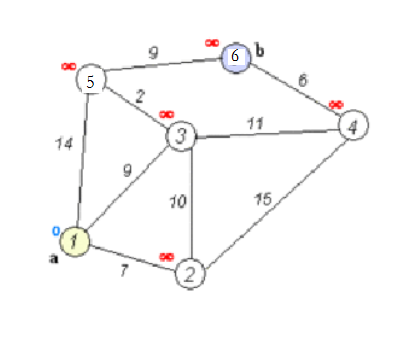
首先,我们先假设所有的点到1的距离都为一个很大的数,例如999999999;
然后对于1这个点,它可以去三个小伙伴的家里(2号、3号、4号),它先到2号家里,发现距离是7,它又依次到3、5号点,分别发现距离是9和14。现在1号点就不打算待在家里了,它比较懒,就去离自己进的2号家里,所以dis[2]更新为7,dis[3]=9,dis[5]=14。
其次,这些点有个特点,就是它们都十分enthusiastic,它会不停的问自己家的邻居(与该点连接的其他点):1号点到你们家用不用先来我家,距离也许更短哦?例如2号点,它不会问1号点,因为1号点已经不在他家了(exist[1]=false),他就去问3,4号。因为9<10+7,所以3号点谢绝说:不了,他直接来我家就是最短的,是9。2号点又去问4号说:哎?1号去你家先到我家坐会呗?因为初始化1到每个点的距离都是999999999,所以7+15肯定小于999999999。所以4说:好啊!,先到你家啊,这样1号点就不累了!,所以dis[4]更新为15+7=22,。当2号点全都问完之后,它也要去干别的事了,所以就退出,即exist[2]=false。
如此循环,直到6号点。
大体的思路就是这样,那么队列是怎么模拟的呢?
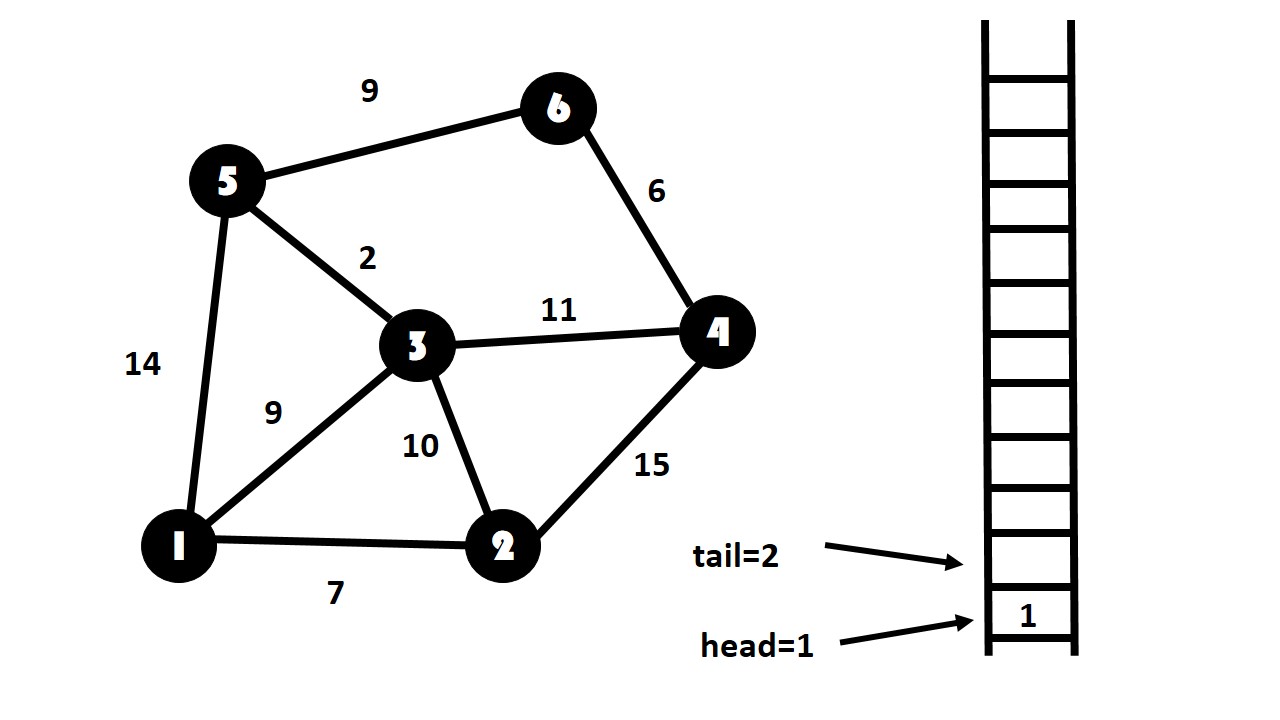
初始化,把1放进队列中,接着,按照顺序把1能走到的点依次放入队列。
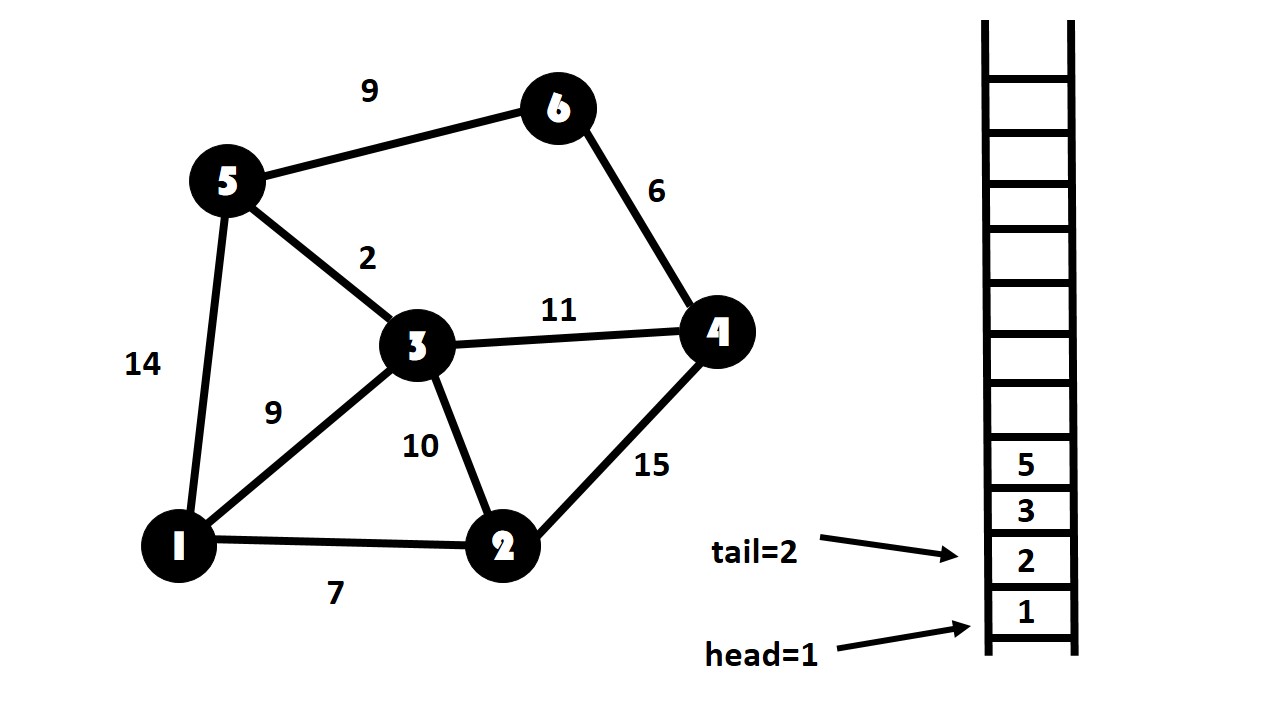
1退出,指针向上移,把2能到达的点依次放入队列中,有过的点就不放。
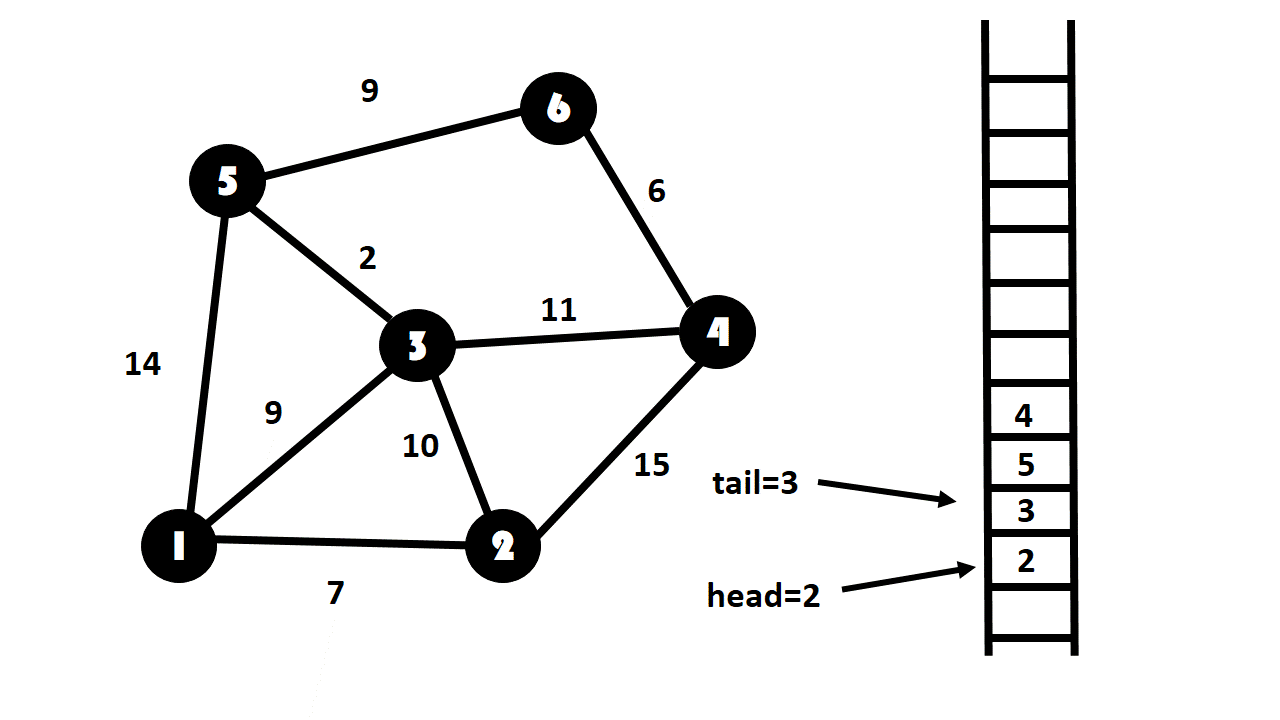
如此循环知道队列里只剩6号点位置。
这就是队列模拟的操作了,代码实现可能会看得更清楚吧:
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cstdlib> const int N=210000; using namespace std; int head,tail,st,z,x,y,len=0; int lis[N]; int last[N]; int dis[N]; bool exist[N]; struct bian {//构造边 int x,y,d,next; }; bian a[1010000]; void zxy(int x,int y,int d) {//定义zxy函数 len++; a[len].x=x; a[len].y=y; a[len].d=d; a[len].next=last[x]; last[x]=len; } int main() { int n,m; scanf("%d%d",&n,&m); for(int i=1; i<=m; i++) { scanf("%d%d%d",&x,&y,&z); zxy(x,y,z);//双向边操作 zxy(y,x,z); } st=1; memset(exist,false,sizeof(exist)); lis[st]=true; for(int i=1; i<=n; i++) dis[i]=99999999; dis[1]=0; head=1; tail=2; while(head!=tail) { x=lis[head]; for(int k=last[x]; k; k=a[k].next) { y=a[k].y; if(dis[y]>dis[x]+a[k].d) { dis[y]=dis[x]+a[k].d; if(exist[y]==false) { exist[y]=true; lis[tail]=y; tail++; if(tail==n+1)//循环队列 tail=1; } } } lis[head]=0; head++; if(head==n+1)//循坏队列 head=1; exist[x]=false; } if(dis[n]==99999999) printf("-1"); else printf("%d",dis[n]); return 0; }