树状数组与线段树的区别是什么呢?
树状数组能有的操作,线段树一定有;
线段树有的操作,树状数组不一定有。
但是,凡是树状数组能进行的操作,速度肯定比线段树的快。
所以,树状数组还是非常实用的。
#include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #include <vector> #include <cstdlib> #define N 10010 #define zxy(i , a , b) for(int i = a ; i <= b ; i ++) #define yxz(i , a , b) for(int i = a ; i >= b ; i --) #define zxyzxy(i , a , b) for(int i = a ; i < b ; i ++) #define yxzyxz(i , a , b) for(int i = a ; i > b ; i --) using namespace std; int read() { int ans = 0; char ch = getchar(),last = ' '; while(ch < '0' || ch > '9') last = ch , ch = getchar(); while(ch >= '0' && ch <= '9') ans = ans * 10 +ch - '0' , ch = getchar(); if(last == '-') ans = -ans; return ans; } void put(int x) { if(x < 0) { putchar('-'); x = -x; } if(x == 0) { putchar('0'); return; } int q[100] , nn = 0; while(x) q[++ nn] = x % 10 , x /= 10; while(nn) putchar('0' + q[nn]), --nn; } int a[N],c[N],n;
先建两个数组:a[]是用来存本来的数的;c[]相当与a[]的若干个上级,他管理的a[]的数随他下标的增大而逐渐增多(这样的好处下面会说)。
那么树状数组的思路是什么呢?
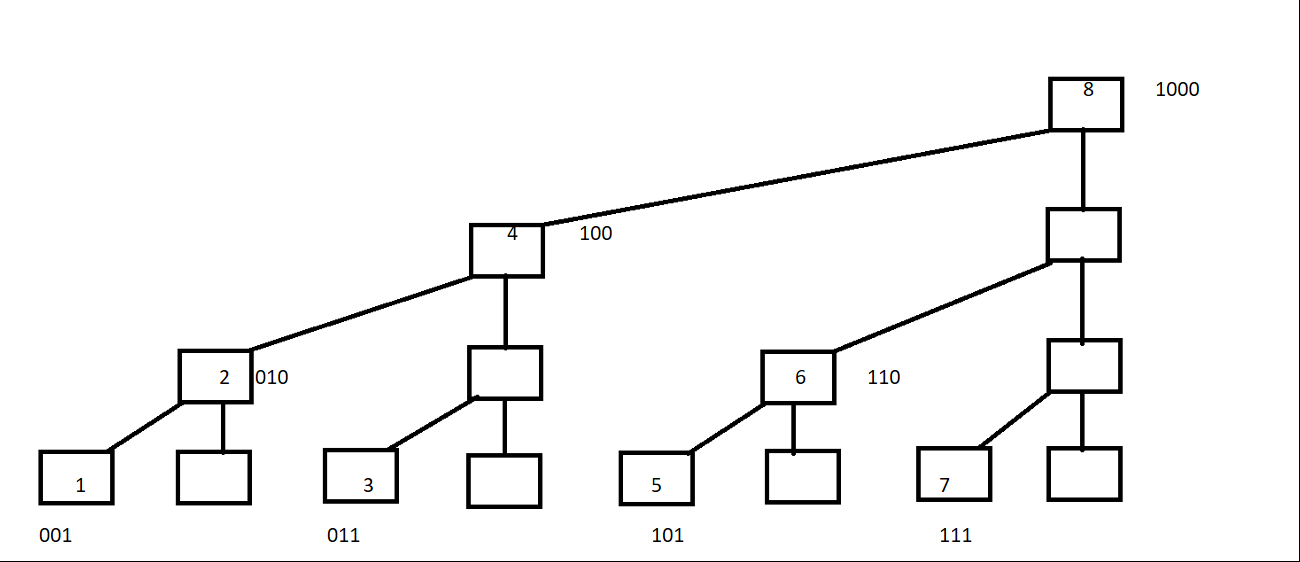
请看这幅图,最下面的八个方块就代表存入a[]中的八个数,现在都是十进制;
他们上面的参差不齐的剩下的方块就代表a[]的上级——c[]数组;
很显然看出:c[2]管理的是a[1] a[2] ;c[4]管理的是a[1] a[2] a[3] a[4] ; c[6]管理的是a[5] a[6] ;c[8]则管理全部8个数。
所以,如果你要算区间和的话,比如说要算a[51] ~ a[91]的区间和,暴力算当然可以,那上百万的数,那就RE喽。
那么这种类似于跳一跳的连续跳到中心点而分值不断变大的原理是一样的。
你从91开始往前跳,发现c[n](n我也不确定是多少,算起来太麻烦,就意思一下)只管a[91]这个点,那么你就会找a[90],发现c[n - 1]管的是a[90] a[89];那么你就会直接跳到a[88] ,c[n - 2]就会管a[81] ~ a[88]这些数,下次查询从a[80]往前找,以此类推。
那么问题来了,你是怎么知道c[]管的a[]的个数分别是多少呢?你那个1个 2个 8个……是怎么来的呢?
这时,我们引入一个函数——lowbit:
int lowbit(int x)//算出x二进制的从右往左出现第一个1以及这个1之后的那些0组成数的二进制对应的十进制的数 { return x & -x; }
lowbit的意思注释说明了,咱们就用这个说法来证明一下a[88]:
88 -> 1011000 B(B代表二进制)
发现第一个1以及他后面的0组成的二进制是 1000
1000 B -> 8
1000对应的十进制是8,所以c[]一共管理8个a[];
这就是lowbit的用处,仅此而已(但也相当有用)。
你可能又问了:x & -x 是什么意思啊?
-x 代表x的负数,计算机中负数使用对应的正数的补码来表示;
例如 :
x =88(1011000);
-x = -88 = (0100111 + 1) = (101000);
x & (-x) = (1000) = 8;
神奇吧,我也觉得神奇!
那么对于单点修改就更轻松了:
void change(int x ,int k) { while(x <= n)//不能越界 { c[x] = c[x] + k; x = x + lowbit(x); } }
每次只要在他的上级那里更新就行,自己就可以不用管了。
int getsum(int x) //a[1]……a[x]的和 { int ans = 0; while(x >= 1) { ans = ans + c[x]; x = x - lowbit(x); } return ans; }
区间和也不用说了吧,代码十分清真。
给一道板题:
【题意】
给出n个数,并且初始化所有数字都为0。接下来m次操作。
操作有以下两种:
1:C x y 把第x个数的值增加y(y可正可负)
2:P x y 就是询问 第x个数 至 第y个数 的所有数的和。
【输入格式】
第一行两个整数n和m(1 <= n <= 100000 ,1 <= m <= 100000 )
下来m行,每行描述一次操作。
【输出格式】
当2操作时输出相应的答案。
【样例输入】
5 3
C 2 3
C 4 5
P 1 5
【样例输出】
8
#include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #include <vector> #include <cstdlib> #define N 10010 #define zxy(i , a , b) for(int i = a ; i <= b ; i ++) #define yxz(i , a , b) for(int i = a ; i >= b ; i --) #define zxyzxy(i , a , b) for(int i = a ; i < b ; i ++) #define yxzyxz(i , a , b) for(int i = a ; i > b ; i --) using namespace std; int read() { int ans = 0; char ch = getchar(),last = ' '; while(ch < '0' || ch > '9') last = ch , ch = getchar(); while(ch >= '0' && ch <= '9') ans = ans * 10 +ch - '0' , ch = getchar(); if(last == '-') ans = -ans; return ans; } void put(int x) { if(x < 0) { putchar('-'); x = -x; } if(x == 0) { putchar('0'); return; } int q[100] , nn = 0; while(x) q[++ nn] = x % 10 , x /= 10; while(nn) putchar('0' + q[nn]), --nn; } int a[N],c[N],n; int lowbit(int x)//算出x二进制的从右往左出现第一个1以及这个1之后的那些0组成数的二进制对应的十进制的数 { return x & -x; } void change(int x ,int k) { while(x <= n)//不能越界 { c[x] = c[x] + k; x = x + lowbit(x); } } int getsum(int x) //a[1]……a[x]的和 { int ans = 0; while(x >= 1) { ans = ans + c[x]; x = x - lowbit(x); } return ans; } int main() { int m; n = read(); m = read(); memset(a , 0 , sizeof(a)); memset(c , 0 , sizeof(c)); zxy(i , 1 , m) { char ss[N]; int x, y; scanf("%s",ss); x = read(); y = read(); if(ss[0] == 'C') change(x , y); else put(getsum(y) - getsum(x - 1)); //因为getsum求的是1到这个数的和,所以求x到y的和就应该用y - (x - 1) } return 0; }