2021.1.13 刷题（最长回文字符串-动规）

题目链接：https://leetcode-cn.com/problems/longest-palindromic-substring/
题目描述：
给你一个字符串 s，找到 s 中最长的回文子串。
示例 1：
输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：
输入：s = "cbbd"
输出："bb"

示例 3：
输入：s = "a"
输出："a"

示例 4：
输入：s = "ac"
输出："a"

提示：
1 <= s.length <= 1000
s 仅由数字和英文字母（大写和/或小写）组成

方法一：暴力求解

class Solution {
public:
    string longestPalindrome(string s) {
        if(s.length()==1)
            return s;
        string rev = s;
        string res;
        std::reverse(rev.begin(),rev.end());
        if(rev == s)
            return s;
        int len = 0;  //回文字串的长度
        for(int i = 0; i < s.length(); i++)   
        {
            string temp;  //待验证字串
            for(int j = i; j < s.length(); j++)
            {
                temp = temp + s[j];
                if(len >= temp.length())
                    continue;
                else if(rev.find(temp)!=-1)  //找到s与rev的最长公共字串temp
                {
                    string q = temp; //验证temp是否是回文字串
                    std::reverse(q.begin(),q.end());
                    if(q == temp)
                    {
                        res = temp;
                        len = temp.length();
                    }     
                }else break;  
            }
            temp = "";
        }
        return res;
    }
};

方法二：动态规划
题解链接：https://leetcode-cn.com/problems/longest-palindromic-substring/solution/5-zui-chang-hui-wen-zi-chuan-dong-tai-gui-hua-jie-/
本题使用的方法是动态规划，这里需要找的是最长回文子串，首先第一步，我们需要定义dp数组的含义，定义二维布尔数组dp[i][j]dp[i][j]数组表示：
字符串s[icdots j]s[i⋯j]是否为回文子串，如果是，dp[i][j] = true，如果不是，dp[i][j] = false。

如何我们现在已经知道了dp[i+1][j-1]了，那我们如何计算dp[i][j]呢？通过观察，我们发现：
如果s[i] == s[j]那么说明只要dp[i+1][j-1]是回文子串，那么是dp[i][j]也就是回文子串
如果s[i]不等于s[j]那么说明dp[i][j]dp[i][j]必定不是回文子串。
当只有一个字母的时候肯定是回文子串，所以初始化的dp表应该如下图所示：

但是这样会有一种情况通过不了例如给的例子中的“cbbd”：

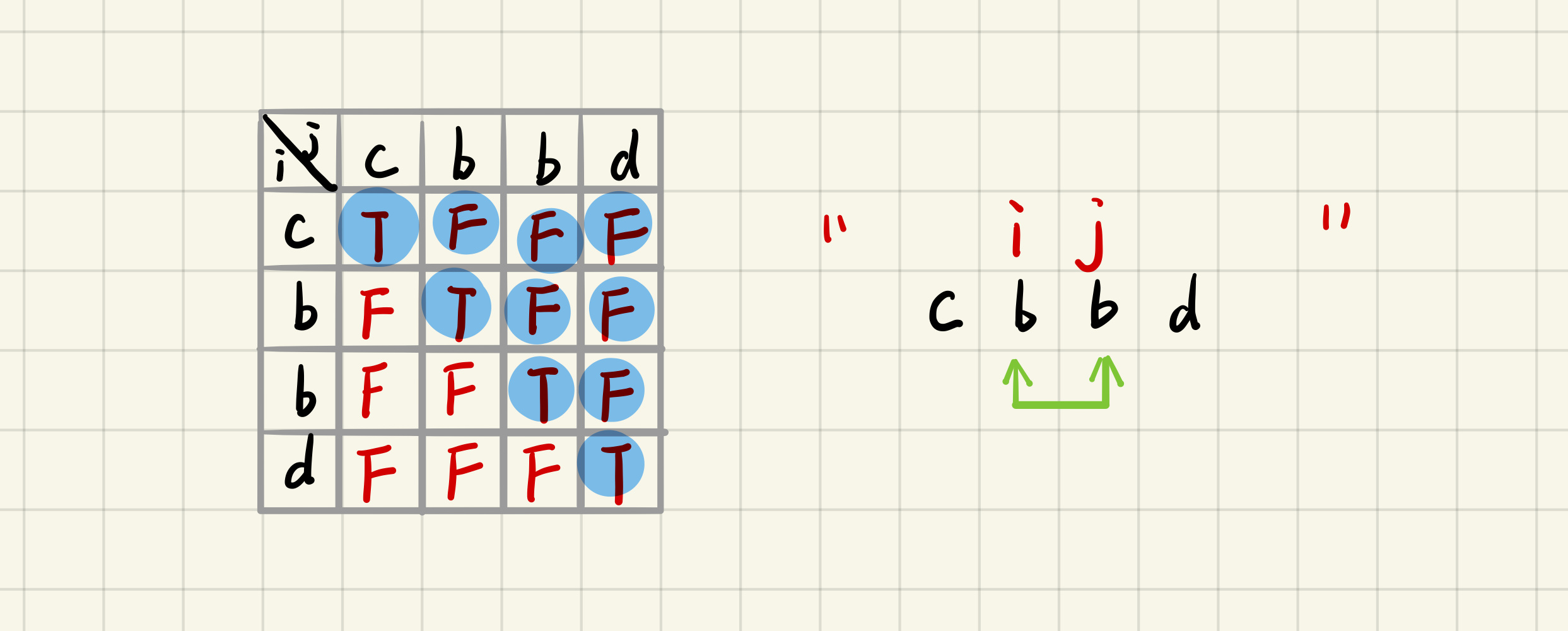
由于我们在dp表中表示不出来，那我们就在计算的时候单独拿出来这种情况计算，即i和j相邻的时候。

class Solution {
public:
    string longestPalindrome(string s) {
        int len=s.size();
        if(len==0||len==1)
            return s;
        int start=0;//回文串起始位置
        int max=1;//回文串最大长度
        vector<vector<int>>  dp(len,vector<int>(len));//定义二维动态数组
        for(int i=0;i<len;i++)//初始化状态
        {
            dp[i][i]=1;
            if(i<len-1&&s[i]==s[i+1])
            {
                dp[i][i+1]=1;
                max=2;
                start=i;
            }
        }
        for(int l=3;l<=len;l++)//l表示检索的子串长度，等于3表示先检索长度为3的子串
        {
            for(int i=0;i+l-1<len;i++)
            {
                int j=l+i-1;//终止字符位置
                if(s[i]==s[j]&&dp[i+1][j-1]==1)//状态转移
                {
                    dp[i][j]=1;
                    start=i;
                    max=l;
                }
            }
        }
        return s.substr(start,max);//获取最长回文子串
    }
};