题目链接:https://leetcode-cn.com/problems/minimum-size-subarray-sum
题目描述:
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
输入:s = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
进阶:如果你已经完成了 O(n) 时间复杂度的解法, 请尝试 O(n log n) 时间复杂度的解法。
解题:
刷题目录:https://github.com/youngyangyang04/leetcode-master
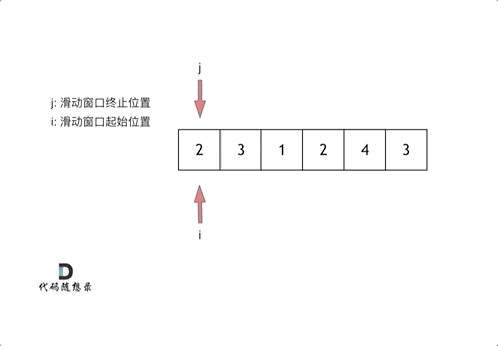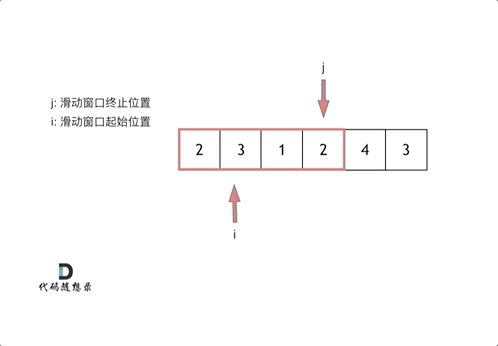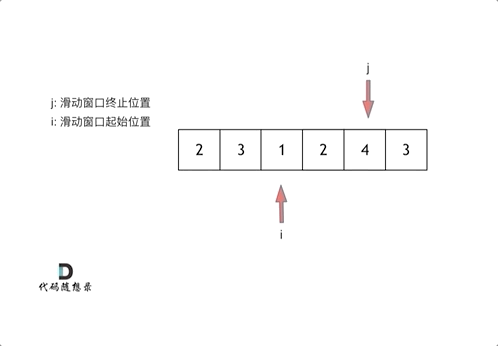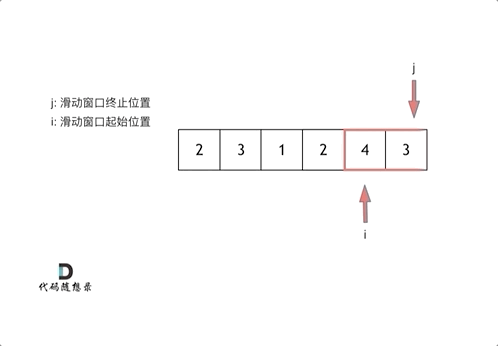
从动画中可以发现滑动窗口也可以理解为双指针法的一种!只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
在本题中实现滑动窗口,主要确定如下三点:
窗口内是什么?
如何移动窗口的起始位置?
如何移动窗口的结束位置?
窗口就是 满足其和 ≥ s 且长度最小的连续子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要缩小,即起始位置向前移动。
窗口的结束位置如何移动:如果当前窗口的值小于s,窗口就要扩大,即结束位置向前移动。
窗口的结束位置就是遍历数组的指针,窗口的起始位置设置为数组的起始位置就可以了。
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int len = nums.size();
int sum = 0; //滑动窗口的数值之和
int fastIndex = 0; //滑动窗口的结束位置
int slowIndex = 0; //滑动窗口的起始位置
int subLength = 0; //滑动窗口的长度
int minLength = nums.size() + 1;
for(; fastIndex < len; fastIndex++)
{
sum += nums[fastIndex];
while(sum >= s) //动态调节滑动窗口的起始位置
{
subLength = fastIndex - slowIndex + 1;
minLength = subLength < minLength ? subLength:minLength;
sum -= nums[slowIndex];
slowIndex++;
}
}
return minLength == nums.size() + 1? 0 : minLength;
}
};