2021.2.9 刷题（构造二叉树）

1.从中序与后序遍历序列构造二叉树
题目链接：https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
题目描述：

题解：

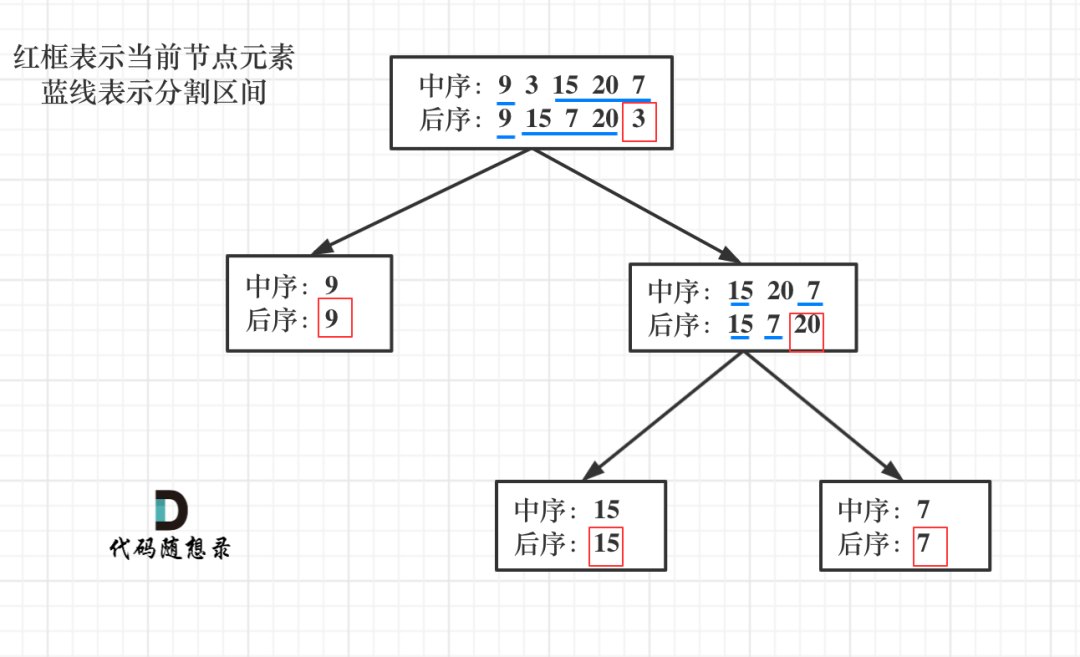
第一步：如果数组大小为零的话，说明是空节点了。
第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
第五步：切割后序数组，切成后序左数组和后序右数组
第六步：递归处理左区间和右区间

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* travel(vector<int>& inorder, vector<int>& postorder)
    {
        if(postorder.size() == 0) return nullptr;
        int val = postorder[postorder.size() - 1]; //二叉树的根
        TreeNode* root = new TreeNode(val);//创建一个新节点
        int index;
        for(index = 0; index < inorder.size(); index++)  //在中序数组中找到后续节点的分割位置
        {
            if(inorder[index] == val) break;
        }
        //切割中序数组，中序左数组[0, index)
        vector<int> leftInorder(inorder.begin(), inorder.begin() + index);
        //切割中序数组，中序右数组[index + 1, end)
        vector<int> rightInorder(inorder.begin() + index + 1, inorder.end());
        postorder.resize(postorder.size() - 1);//去除后序数组的最后一个元素
        //切割后序数组，后序左数组于中序左数组大小一致
        vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
        vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
        //递归处理左右子树
        root->left = travel(leftInorder, leftPostorder);
        root->right = travel(rightInorder, rightPostorder);
        return root;

    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.size() == 0 || postorder.size() == 0)
            return nullptr;
        return travel(inorder, postorder);

    }
};

2.从前序与中序遍历序列构造二叉树
题目链接：https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
题目描述：

题解：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* travel(vector<int>& preorder, int preBegin, int preEnd, vector<int>& inorder, int inBegin, int inEnd)
    {
        
        if(preBegin == preEnd) return NULL;
        int val = preorder[preBegin];
        TreeNode* root = new TreeNode(val);
        if (preEnd - preBegin == 1) return root;
        int index;//查找切割点
        for(index = inBegin; index < inEnd; index++)
        {
            if(inorder[index] == val) break;
        }
        //切割中序序列
        int leftInorderBegin = inBegin;
        int leftInorderEnd = index;
        int rightInorderBegin = index + 1;
        int rightInorderEnd = inEnd;
        //切割前序序列
        int leftPreorderBegin = preBegin + 1;
        int leftPreorderEnd = preBegin + 1 + leftInorderEnd - leftInorderBegin;
        int rightPreorderBegin = leftPreorderEnd;
        int rightPreorderEnd = preEnd;
        //递归左、右子树
        root->left = travel(preorder, leftPreorderBegin, leftPreorderEnd, inorder, leftInorderBegin, leftInorderEnd);
        root->right = travel(preorder, rightPreorderBegin, rightPreorderEnd, inorder, rightInorderBegin, rightInorderEnd);

        return root;

    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size() == 0 || inorder.size() == 0)
            return nullptr;
        return travel(preorder, 0, preorder.size(), inorder, 0, inorder.size());
    }
};