参考:http://www.felix021.com/blog/read.php?2040
以上参考的原文写得很好,解析的非常清楚。以下用我自己的理解,对关键部分算法进行简单的描述:
- 回文的判断需要完成从中心字符向两侧进行逐字符匹配;
- 回文好比圆,由两个重要的参数决定,即“圆心”(中心字符,对偶数长的回文而言是两个字符)和“直径”(回文长度);
- 如果一个“点”落入另一个“圆”内,则以这个点为圆心的“圆”必定受这个“大圆”及相对大圆圆心对称的“对称圆”的影响:
- 在“大圆”范围内,这个“圆”的直径不能大于“对称圆”的直径(只要在大回文的范围内,该回文的字符匹配结果可以取用对称位置回文的匹配结果);
- 即使“对称圆”超出“大圆”边界,这个“圆”也不能超出“大圆”边界(如果对称位置回文长度超出了大回文范围,则该回文不可超出范围,否则大回文需要延展,即大圆需要扩张);
盗两张图:
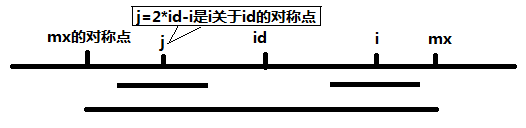
对称回文在大回文范围内
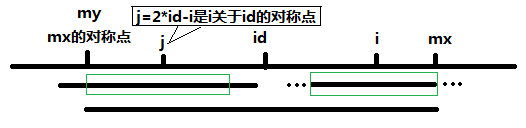
对称回文超出大回文范围
这个算法巧妙利用了回文的特点,在线性求解过程中充分利用了之前已得到的结果,尽量避免重复匹配,极大降低复杂度。
string = "12212321"
SEPCHAR = '#'
target = ""
# pre-process
for i in range(len(string)):
target = target + SEPCHAR + string[i]
target=target + SEPCHAR
# the key procedure
idx = 0
mx = 0
p=[]
for i in range(len(target)):
p.append(0)
for i in range(len(target)):
if i >= mx:
p[i] = 1
else:
p[i] = min(p[2*idx-i], mx-i)
while (i+p[i]) in range(len(target)) and (i-p[i]) in range(len(target)) and target[i+p[i]] == target[i-p[i]]:
p[i] += 1
if (i + p[i] > mx):
mx = i + p[i]
idx = i
# print the results
print string
for i in range(len(target)):
print target[i],
print ""
max_len = 0
center = 0
for i in range(len(target)):
print p[i],
if p[i] > max_len:
max_len = p[i]
center = i
print ""
print "max len of palindrom is %d at index %d" %(max_len-1, center/2)