BZOJ 1101: [POI2007]Zap

二次联通门 : BZOJ 1101: [POI2007]Zap

二次联通门 :  luogu P3455 [POI2007]ZAP-Queries

 求下面式子的值

因为 x∈[1,a], y∈[1,b]

那么 x/k∈[1,a/k], y/k∈[1,b/k]

则有以下式子

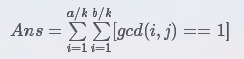
因为

所以

我们把 μ(i)  放到前面去， 交换一下枚举的顺序得到以下的式子

这个式子就变成这样了

 因为有这只有种取值

所以下底函数分块，前缀和优化下就能过了。

 弃了弃了。。。果然自己太笨。。反演看一上午看不明白。。

/*
    BZOJ 1101: [POI2007]Zap
    
    莫比乌斯反演
    
    
*/
#include <cstdio>

void read (int &now)
{
    register char word = getchar ();
    bool temp = false;
    for (now = 0; word < '0' || word > '9'; word = getchar ());
    for (; word >= '0' && word <= '9'; now = now * 10 + word - '0', word = getchar ());
}

inline void swap (int &a, int &b)
{
    int now = a;
    a = b;
    b = now;
}

inline int min (int a, int b)
{
    return a < b ? a : b;
}

#define Max 100005

bool is_prime[Max];
int prime_list[Max];

int mobius[Max];

int sum[Max];

void Euler_to_Mobius (int N)
{
    is_prime[0] = is_prime[1] = true;
    mobius[1] = 1;
    int Prime_Count = 0;
    for (register int i = 2, j, pos; i <= N; i ++)
    {
        if (!is_prime[i])
        {
            prime_list[++ Prime_Count] = i;
            mobius[i] = -1;
        }
        for (j = 1; j <= Prime_Count && i * prime_list[j] <= N; j ++)
        {
            pos = i * prime_list[j];
            is_prime[pos] = true;
            if (i % prime_list[j])
                mobius[pos] = -mobius[i];
            else
            {
                mobius[pos] = 0;
                break;
            }    
        }
    }
}


int main (int argc, char *argv[])
{
    int T;
    read (T);
    int _Limit = Max - 2;
    Euler_to_Mobius (_Limit);
    
    for (int i = 1; i <= _Limit; i ++)
        sum[i] = sum[i - 1] + mobius[i];
    
    long long Answer = 0;
    
    for (int x, y, z; T --; Answer = 0)
    {
        read (x);
        read (y);
        read (z);
        
        x /= z;
        y /= z;

        if (x > y) 
            swap (x, y);
        for (register int j = 0, i = 1; i <= x; i = j + 1)
        {
            j = min (x / (x / i), y / (y / i));
            Answer += 1LL * (sum[j] - sum[i - 1]) * (x / i) * (y / i);
        }
        
        printf ("%lld
", Answer);
    }
    
    return 0;
}