BZOJ 3771: Triple

二次联通门 : BZOJ 3771: Triple

依旧是权限题放题面

/*
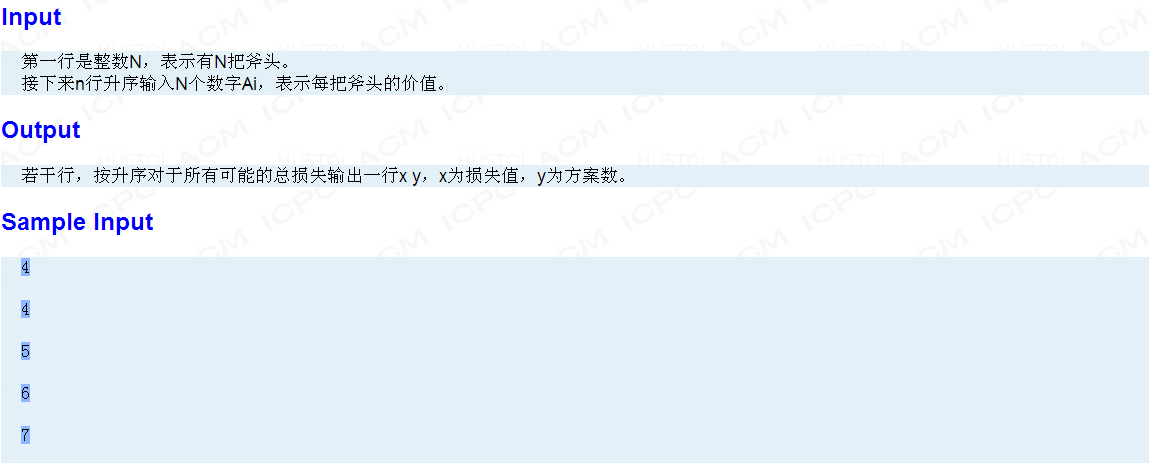
    BZOJ 3771: Triple
    
    考虑构造三个生成函数

    A为原斧子价值的生成函数
    B为斧子价值两倍的生成函数
    C为斧子价值三倍的生成函数
    即一次拿1/2/3把

    然后直接乘的话是会出现重复的
    所以要进行一下容斥

    最终的多项式即为A+(A*A-B)/2+(A*A*A-3*A*B+2*C)/6
    发现直接算是O(N^2)的，所以用FFT加速
*/
#include <cstdio>
#include <iostream>
#include <cmath>
 
#define rg register
inline void read (int &n)
{
    rg char c = getchar ();
    for (n = 0; !isdigit (c); c = getchar ());
    for (; isdigit (c); n = n * 10 + c - '0', c = getchar ());
}
typedef double flo; const flo PI = acos (-1.0);
 
struct vec 
{
    flo x, y; vec (flo a = 0, flo b = 0) : x (a), y (b) { }
     
    vec operator + (const vec &rhs)
    { return vec (x + rhs.x, y + rhs.y); }
 
    vec operator - (const vec &rhs)
    { return vec (x - rhs.x, y - rhs.y); }
 
    vec operator * (const vec &rhs)
    { return vec (x * rhs.x - y * rhs.y, x * rhs.y + y * rhs.x); }
 
    vec operator /= (const flo &k)
    { return x /= k, y /= k, *this; }
 
    vec operator * (flo k)
    { return vec (x * k, y * k); }
 
    vec operator / (const flo &k)
    { return vec (x / k, y / k); }
};
#define Max 1000005
int rd[Max]; vec a[Max], b[Max], c[Max];
 
void DFT (vec *a, int N, int f = 1)
{
    rg int i, j, k; vec wn, w, x, y;
    for (i = 0; i < N; ++ i) if (rd[i] > i) std :: swap (a[i], a[rd[i]]);
     
    for (k = 1; k < N; k <<= 1)
    {
        wn = vec (cos (PI / k), f * sin (PI / k));
        for (j = 0; j < N; j += k << 1)
            for (i = 0, w = vec (1, 0); i < k; ++ i, w = w * wn)
                x = a[i + j], y = a[i + j + k] * w, a[i + j] = x + y, a[i + j + k] = x - y;
    }
    if (f == -1) for (i = 0; i < N; ++ i) a[i] /= N; 
}
 
inline void cmax (int &a, int b) { if (b > a) a = b; }
 
int main (int argc, char *argv[])
{
    int N, L, x; read (N); rg int i; L = N;
    for (; L; -- L)
        read (x), ++ a[x].x, ++ b[x << 1].x, ++ c[x * 3].x, cmax (N, x * 3);
     
    int M = N << 1; L = 0;
    for (N = 1; N <= M; N <<= 1, ++ L); 
     
    for (i = 1; i < N; ++ i)
        rd[i] = (rd[i >> 1] >> 1) | ((i & 1) << (L - 1));
 
    DFT (a, N), DFT (b, N), DFT (c, N);
 
    for (i = 0; i < N; ++ i)
        a[i] = a[i] + (a[i] * a[i] - b[i]) / 2 + (a[i] * a[i] * a[i] - a[i] * b[i] * 3 + c[i] * 2) / 6;
 
    DFT (a, N, -1);
 
    for (i = 0; i < N; ++ i)
        if (int (a[i].x + 0.1))
            printf ("%d %d
", i, int (a[i].x + 0.1));
 
    return 0;
}