进阶之常见算法和算法题

一、常用进阶算法

1、二分查找

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

二分查找的基本思想是将n个元素分成大致相等的两部分，取a[n/2]与x做比较，如果x=a[n/2],则找到x,算法中止；如果x<a[n/2],则只要在数组a的左半部分继续搜索x,如果x>a[n/2],则只要在数组a的右半部搜索x.

时间复杂度无非就是while循环的次数！

总共有n个元素，

渐渐跟下去就是n,n/2,n/4,....n/2^k（接下来操作元素的剩余个数），其中k就是循环的次数

由于你n/2^k取整后>=1

即令n/2^k=1

可得k=log2n,（是以2为底，n的对数）

所以时间复杂度可以表示O(h)=O(log2n)

 

方法一：不使用递归

def search(lst, num):
    left = 0
    right = len(lst) - 1
    while left <= right:  # 循环条件
        mid = (left + right) // 2  # 获取中间位置，数字的索引
        if num < lst[mid]:  # 如果查询数字比中间数字小，那就去中间数的左边找，
            right = mid - 1  # 调整右边边界
        elif num > lst[mid]:  # 如果查询数字比中间数字大，那么就去中间数的右边找
            left = mid + 1  # 调整左边边界
        elif num == lst[mid]:
            print('找到的数：%s, 索引是：%s' %(lst[mid], mid))
            return mid  # 如果查询数字刚好为中间值，返回该值得索引
    print('没有找到该值')
    return -1  # 如果循环结束，左边大于了右边，代表没有找到


lst = [1, 3, 4, 8, 11, 12, 13, 15, 17, 20, 21, 27, 42, 43, 49, 51, 52, 57, 58, 59, 62, 69, 71, 73, 74, 80, 83, 84, 89, 96, 100, 111]
search(lst, 1)  # 找到的数：1, 索引是：0
search(lst, 51)  # 找到的数：51, 索引是：15
search(lst, 96)  # 找到的数：96, 索引是：29
search(lst, 120)  # 没有找到该值

方法二：使用递归

def search(lst, num, left=None, right=None):
    left = 0 if left is None else left
    right = len(lst)-1 if right is None else right
    mid = (right + left) // 2
    if left > right:  # 循环结束条件
        print('没有找到该值')
        return None
    elif num < lst[mid]:
        return search(lst, num, left, mid - 1)
    elif num > lst[mid]:
        return search(lst, num, mid + 1, right)
    elif lst[mid] == num:
        print('找到的数：%s, 索引是：%s' % (lst[mid], mid))
        return mid


lst = [1, 3, 4, 8, 11, 12, 13, 15, 17, 20, 21, 27, 42, 43, 49, 51, 52, 57, 58, 59, 62, 69, 71, 73, 74, 80, 83, 84, 89, 96, 100, 111]
search(lst, 1)  # 找到的数：1, 索引是：0
search(lst, 51)  # 找到的数：51, 索引是：15
search(lst, 96)  # 找到的数：96, 索引是：29
search(lst, 120)  # 没有找到该值

2、二叉查找树-平衡树

前置知识：二叉树的深度

# 节点定义如下
# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
n3 = TreeNode(3)
n9 = TreeNode(9)
n20 = TreeNode(20)
n15 = TreeNode(15)
n7 = TreeNode(7)

n3.left = n9
n3.right = n20
n20.left = n15
n20.right = n7
n3 = TreeNode(3)
n9 = TreeNode(9)
n20 = TreeNode(20)
n15 = TreeNode(15)
n7 = TreeNode(7)

n3.left = n9
n3.right = n20
n20.left = n15
n20.right = n7
Solution().maxDepth(n3)

# 方法一：每到一个节点，深度就+1
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        return self.get_dep(root, 1)

    def get_dep(self, node, depth):
        if not node:
            return depth - 1
        return max(self.get_dep(node.left,depth+1),self.get_dep(node.right,depth+1))


# 方法二：
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        else:
            left_depth = self.maxDepth(root.left)
            right_depth = self.maxDepth(root.right)
        return max(left_depth,right_depth)+1

算法解析：
终止条件： 当 root​ 为空，说明已越过叶节点，因此返回 深度 0 。
递推工作： 本质上是对树做后序遍历，从叶子节点一层层向上加
计算节点 root​ 的 左子树的深度 ，即调用 maxDepth(root.left)；
计算节点 root​ 的 右子树的深度 ，即调用 maxDepth(root.right)；
返回值： 返回 此树的深度 ，即 max(maxDepth(root.left), maxDepth(root.right)) + 1。

判断这个二叉树是否为平衡二叉树

# 方法一
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        if not root:
            # 空树也是平衡树
            return True
        left_height = self.get_dep(root.left, 1)
        right_height = self.get_dep(root.right, 1)
        if abs(left_height-right_height) > 1:
            return False
        else:
            return self.isBalanced(root.left) and self.isBalanced(root.right)

    def get_dep(self, node, depth):
        if not node:
            return depth - 1
        return max(self.get_dep(node.left,depth+1),self.get_dep(node.right,depth+1))


# 方法二
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        if not root:
            return True

        left_height = self.depth(root.left)
        right_height = self.depth(root.right)
        if abs(left_height - right_height) > 1:
            return False
        else:
            return self.isBalanced(root.left) and self.isBalanced(root.right)

    def depth(self, root):
        if not root: 
            return 0

        return max(self.depth(root.left), self.depth(root.right)) + 1

3、二叉树遍历算法

原文更详细哦
作者：z1m
链接：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/solution/tu-jie-er-cha-shu-de-si-chong-bian-li-by-z1m/

来源：力扣（LeetCode）

# 前序遍历
# 递归
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        def tree(node):
            if not node:
                return
            res.append(node.val)
            tree(node.left)
            tree(node.right)
        tree(root)
        return res


# 迭代
class Solution:
    """
    它先将根节点 cur 和所有的左孩子入栈并加入结果中，直至 cur 为空，用一个 while 循环实现：
    然后，每弹出一个栈顶元素 tmp，就到达它的右孩子，再将这个节点当作 cur 重新按上面的步骤来一遍，直至栈为空。这里又需要一个 while 循环。
    """
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        
        cur, stack, res = root, [], []
        while cur or stack:
            while cur:  # 根节点和左孩子入栈
                res.append(cur.val)
                stack.append(cur)
                cur = cur.left
            tmp = stack.pop()  # 每弹出一个元素，就到达右孩子
            cur = tmp.right
        return res



# 中序遍历
# 递归
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        def tree(node):
            if not node:
                return
            tree(node.left)
            res.append(node.val)
            tree(node.right)
        tree(root)
        return res



# 迭代
class Solution:
    """
    和前序遍历的代码完全相同，只是在出栈的时候才将节点 tmp 的值加入到结果中。
    """
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        
        cur, stack, res = root, [], []
        while cur or stack:
            while cur:  # 根节点和左孩子入栈
                stack.append(cur)
                cur = cur.left
            tmp = stack.pop()
            res.append(cur.val)  # 出栈再加入结果
            cur = tmp.right
        return res


# 后续遍历
# 递归
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        res = []
        def tree(node):
            if not node:
                return
            tree(node.left)
            tree(node.right)
            res.append(node.val)
        tree(root)
        return res



# 迭代
class Solution:
    """
    继续按照上面的思想，这次我们反着思考，节点 cur 先到达最右端的叶子节点并将路径上的节点入栈；
    然后每次从栈中弹出一个元素后，cur 到达它的左孩子，并将左孩子看作 cur 继续执行上面的步骤。
    最后将结果反向输出即可。参考代码如下：
    """
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        
        cur, stack, res = root, [], []
        while cur or stack:
            while cur:  # 先达最右端
                res.append(cur.val)
                stack.append(cur)
                cur = cur.right
            tmp = stack.pop()
            cur = tmp.left
        return res[::-1]

4、广度搜索算法

BFS(Breadth First Search)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        
        res = []
        stack = [root, ]  # 进行遍历的节点顺序
        while stack:
            level = []  # 每层的节点都存在一起
            n = len(stack)  # 每层需要处理的节点数
            for _ in range(n):
                node = stack.pop(0)  # 当前处理的节点
                level.append(node.val)
                if node.left:
                    stack.append(node.left)
                if node.right:
                    stack.append(node.right)
            if level:
                res.append(level)
        return res

5、深度搜索算法

作者：fuxuemingzhu
链接：https://leetcode-cn.com/problems/binary-tree-level-order-traversal/solution/tao-mo-ban-bfs-he-dfs-du-ke-yi-jie-jue-by-fuxuemin/
来源：力扣（LeetCode）

DFS(Depth First Search)不是按照层次遍历的。为了让递归的过程中同一层的节点放到同一个列表中，在递归时要记录每个节点的深度 level。递归到新节点要把该节点放入 level 对应列表的末尾。

当遍历到一个新的深度 level，而最终结果 res 中还没有创建 level 对应的列表时，应该在 res 中新建一个列表用来保存该 level 的所有节点。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def levelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        res = []
        self.level(root, 0, res)
        return res

    def level(self, root, level, res):
        if not root: 
            return
        
        if len(res) == level:
            # 如果有3层，res就会有三个列表元素
            # 每个列表存放自己层次的节点(level层次对应res的索引)
            res.append([])
        
        res[level].append(root.val)
        if root.left:
            self.level(root.left, level + 1, res)
        if root.right:
            self.level(root.right, level + 1, res)

二、算法题

说明：题目来自LeetCode和牛客网

LeetCode：https://leetcode-cn.com/

牛客网：https://www.nowcoder.com/

1、

小明有一些气球想挂在墙上装饰 他希望相同颜色的气球不要挂在一起 写一个算法帮他得出一种可行的挂气球方式 自行定义函数 输入和返回 如果无法做到相同颜色的气球不挂在一起 请定义合适的异常方式返回

"""
小明有一些气球想挂在墙上装饰
他希望相同颜色的气球不要挂在一起
写一个算法帮他得出一种可行的挂气球方式
自行定义函数 输入和返回 如果无法做到相同颜色的气球不挂在一起 请定义合适的异常方式返回
"""
def sort_ball(data):
    """
    :param data: dict类型
    :return: 
    """
    all_count = sum(data.values())  # 气球总数
    # 根据data的值，获取气球颜色最多的数量
    max_count = sorted(data.items(), key=lambda x: x[1], reverse=True)[0][1]

    # 异常：即相同颜色的气球挂在一起了
    if max_count - 1 > all_count - max_count:
        return '无法做到相同气球不挂在一起！'

    # 初始的气球列表(顺序的)
    initial_lst = []
    for ball, count in data.items():
        initial_lst.extend([ball for i in range(count)])

    # 排序后，相同气球不挂一起
    res_lst = ["null"] * all_count  # 初始化最终列表的长度
    # 排序思路：间隔地把气球放到最终的列表
    res_lst[::2] = initial_lst[all_count // 2:]
    res_lst[1::2] = initial_lst[:all_count // 2]
    return res_lst


data = {
    'red': 5,  # 红色气球5个
    'blue': 5,  # 蓝色5个
    'white': 2,  # 白色2个
}
ret = sort_ball(data)
print(ret)  # blue-red-blue-red-blue-red-blue-red-white-red-white-blue

2、计算每个元素除自己之外其他元素的乘积(不能够使用除法)

输入: [1,2,3,4]
输出: [24,12,8,6]

# 1.时间复杂度O(n^2)
def func(lst):
    result_lst = []
    for i in lst:
        tmp_res = 1

        for j in lst:
            if j != i:
                tmp_res *= j

        result_lst.append(tmp_res)
    return result_lst

# 2.时间复杂度O(n)
解题思路:
0.左右乘积列表，这里需要先构造 left，right 两个数组，分别存储当前元素左侧的乘积以及右侧的乘积。
1.初始化两个数组 left，right。其中 left[i] 表示 i 左侧全部元素的乘积。right[i] 表示 i 右侧全部元素的乘积。
2.开始填充数组。这里需要注意 left[0] 和 right[lenght-1] 的值（length 表示数组长度，right 数组是从右侧往左进行填充）。
    对于 left 数组而言，left[0] 表示原数组索引为 0 的元素左侧的所有元素乘积，这里原数组第一位元素左侧是没有其他元素的，所以这里初始化为 1。而其他的元素则为：left[i] = left[i-1] * nums[i - 1]
    同样的 right 数组，right[length-1] 表示原数组最末尾的元素右侧所有元素的乘积。但因为最末尾右侧没有其他元素，所以这里 right[length-1] 也初始化为 1。其他的元素则为：right[i]=right[i+1]*nums[i+1]
3.至于返回数组 output 数组，再次遍历原数组，索引为 i 的值则为：output[i] = left[i] * right[i]


def func(lst):
    length = len(lst)  # 列表长度

    # 初始化左右两个列表和最终输出列表
    left = [1] * length
    right = [1] * length
    output = [1] * length

    # 先填充 left 数组
    # left 数组表示遍历时 i 左侧的乘积
    # 因为数组第一个元素左侧没有其他元素，所以 left 数组第一个元素为 1
    # left 数组接下来的元素则为原数组的第一位元素与 left 数组第一位元素的乘积，依次类推
    for i in range(1, length):
        left[i] = left[i - 1] * lst[i - 1]  # left = [1, 1, 2, 6]

    # 同样的 right 数组从右往左进行填充
    # 同样数组末尾元素右侧没有其他元素，所以末尾元素值为 1
    # 右边往左的元素则为原数组与 right 数组末尾往前一位元素的乘积，依次类推
    for i in range(length - 2, -1, -1):
        right[i] = right[i + 1] * lst[i + 1]

    # 重新遍历，输出 output 数组
    # output[i] 等于 lst 中除 lst[i] 之外其余各元素的乘积
    # 也就是 output[i] 的值为 left[i] * right[i]
    for i in range(length):
        output[i] = left[i] * right[i]

    return output

3、最小公倍数

正整数A和正整数B 的最小公倍数是指 能被A和B整除的最小的正整数值，设计一个算法，求输入A和B的最小公倍数。

"""分析：最小公倍数=两个数的乘积/最大公约数

欧几里德算法又称辗转相除法 --- 求最大公约数
假如需要求 1997 和 615 两个正整数的最大公约数,用欧几里德算法，是这样进行的：
1997 / 615 = 3 (余 152)  # 第一步：两个数相除得到商和余数
615 / 152 = 4(余7)  # 第二步：用上面的除数去除以余数，得到新的商和余数
152 / 7 = 21(余5)  # 重复2的步骤
7 / 5 = 1 (余2)
5 / 2 = 2 (余1)
2 / 1 = 2 (余0)  # 直到余数为0，当前除数就是最大公约数
至此，最大公约数为1
以除数和余数反复做除法运算，当余数为 0 时，取当前算式除数为最大公约数，所以就得出了 1997 和 615 的最大公约数 1。

"""
def max_com_div(x, y):
    """使用辗转相除法求最大公约数"""
    if x > y:
        a = x  # 被除数
        b = y  # 除数
    else:
        a = y  # 被除数
        b = x  # 除数

    # 辗转相除法
    while b != 0:
        c = a % b  # 余数
        a = b
        b = c

    return a


def min_com_multi(x, y):
    """最小公倍数=两个数的乘积/最大公约数"""
    max_com = max_com_div(x, y)
    result = x * y / max_com
    return result

4、计算一个数字的立方根，不使用库函数

def cube_root(x):
    """
    216的立方根，其实就是216的1/3次方
    """
    num = float(x)
    res = num ** (1 / 3.0)
    return '%.1f' % res

5、将一个字符串str的内容颠倒过来，并输出

str的长度不超过100个字符。 如：输入“I am a student”，输出“tneduts a ma I”。
输入描述:
输入一个字符串，可以有空格

输出描述:
输出逆序的字符串

# 最简单的方法，切片逆序
def reverse_order1(s):
    return s[::-1]


# 递归
def reverse_order2(s, last_index):
    """
    :param s: 输入的字符串
    :param last_index: 字符串最后一位索引
    从最后一位索引开始取值，向前拼接
    """
    if last_index < 0:
        return ""
    return s[last_index] + reverse_order2(s, last_index - 1)


res = reverse_order2("I am a student", len("I am a student") - 1)

6、统计个数和平均值

从输入任意个整型数，统计其中的负数个数并求所有非负数的平均值，结果保留一位小数，如果没有非负数，则平均值为0,本题有多组输入数据，输入到文件末尾，请使用while(cin>>)读入

示例1
输入
-13 -4 -7

输出
3
0.0

import sys


while True:
    input_num = sys.stdin.readline().strip()
    num_list = map(int, input_num.split())
    if input_num:
        positive = 0  # 正数个数
        negative = 0  # 负数个数

        positive_sum = 0  # 正数总值
        for num in num_list:
            if num < 0:
                negative += 1
            else:
                positive += 1
                positive_sum += num

        print(negative)
        if positive == 0:
            print(0.0)
        else:
            avg = (float(positive_sum) / positive)
            print("%.1f" % avg)
    else:
        break

7、

连续输入字符串(输出次数为N,字符串长度小于100)，请按长度为8拆分每个字符串后输出到新的字符串数组，

长度不是8整数倍的字符串请在后面补数字0，空字符串不处理。

首先输入一个整数，为要输入的字符串个数。

例如：

输入：

2

abc

12345789

输出：

abc00000

12345678

90000000

import sys

while True:
    n = sys.stdin.readline().strip()
    if n:
        n = int(n)
        while n > 0:
            n -= 1
            str = sys.stdin.readline().strip()
            # 先判断输入的字符串是否为8的倍数，若不是，则先在后面补充0
            # 比如输入str = abc，那么先把str补充0，补到为8的倍数，str = abc00000
            s_length = len(str)
            if s_length % 8 > 0:
                str = str + (8 - s_length % 8) * "0"

            # 对补充完的str每8位输出一次
            item = ""
            for i in range(len(str)):
                item += str[i]
                if (i + 1) % 8 == 0:
                    print(item)
                    item = ""
    else:
        break

8、最长上升子序列

Redraiment是走梅花桩的高手。Redraiment总是起点不限，从前到后，往高的桩子走，要求走的步数最多，你能替Redraiment研究他最多走的步数吗？ 

样例输入

6

2 5 1 5 4 5

样例输出

3

提示：其实就是求最长上升子序列

Example: 
6个点的高度各为 2 5 1 5 4 5 
如从第1格开始走,最多为3步, 2 4 5   # 即从2开始，找到上升的序列，如 2 5是不对的，下降的，但是 2 ... 4 5 就可以，是上升的
从第2格开始走,最多只有1步,5 
而从第3格开始走最多有3步,1 4 5 
从第5格开始走最多有2步,4 5

所以这个结果是3。

def length_of_lis(nums):
    """
    要注意的是：最大上升子序列中的元素可以不是连续的，比如：2 3 1 5 3 最大上升子序列是： 2 3 5
    用dp[i] 表示 从下标0 到下标i 的最长上升子序列的长度，
    例如对于样例输入[10,9,2,5,3,7,101,18], 初始化 dp = [ 1, 1, 1, 1, 1, 1, 1, 1]
    显然dp[0] = 1

    对于任意的i 不为零的情况，应该在 i 的左侧找一个下标 j ，解释：
    1. nums[j]比 nums[i] 小
    2. 证明j这个序列上还有一个上升元素i，那么从0到i的序列中最大的上升序列就是 j的上升序列长度+1
    3. 更新i对应的上升序列长度：dp[i] = max(dp[j]) + 1 , dp[i])

    如果不存在这样的下标j，说明在0 ~ i 的范围内，所有元素都比nums[i] 大，即无法找到一个能和 nums[i] 组成上升子序列的元素。
    """
    lenth = len(nums)
    # 初始化dp
    dp = [1 for _ in range(lenth)]

    for i in range(1, lenth):
        for j in range(i):
            if nums[i] > nums[j]:
                # 0-i这个序列中，可能有多个上升序列，拿到最大的那个长度
                dp[i] = max(dp[j] + 1, dp[i])

    return max(dp)

9、按个数大小输出顺序

输入一个字符串，对字符中的各个英文字符，数字，空格进行统计（可反复调用）
按照统计个数由多到少输出统计结果，如果统计的个数相同，则按照ASCII码由小到大排序输出。

输入：aadddccddc

输出：dca

def my_sorted(string):
    dic = dict()
    for s in string:
        # 如果是数字、字母、空格，统计其数量
        if s.isdigit() or s.isalpha() or s == ' ':
            if s in dic.keys():
                dic[s] += 1
            else:
                dic[s] = 1
    # 第一次排序，按照acsii排序
    tmp = sorted(dic.items(), key=lambda x: x[0])
    # 第二次排序，按照各个字符统计的数量排序
    res = sorted(tmp, key=lambda x: x[1], reverse=True)
    result = ''.join([k for k, v in res])
    return result

10、接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例：

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

解题思路：

作者：xiao_shi_mei
链接：https://leetcode-cn.com/problems/trapping-rain-water/solution/shuang-zhi-zhen-an-xing-qiu-geng-hao-li-jie-onsuan/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

1. 利用左右指针的下标差值计算出每一行雨水+柱子的体积，如图第一行体积为11，第二行为8，第三行为1。累加得到整体体积tmp=20tmp=20（每一层从左边第一个方格到右边最后一个方格之间一定是被蓝黑两种颜色的方格填满的，不会存在空白，这也是为什么能按层求的关键）
2. 计算柱子体积，为height：[0,1,0,2,1,0,1,3,2,1,2,1]height：[0,1,0,2,1,0,1,3,2,1,2,1] 数组之和SUM=14SUM=14（也可以直接用sum()函数，不过时间复杂度就是O(2n)了）
3. 返回结果 tmp-SUMtmp−SUM就是雨水的体积

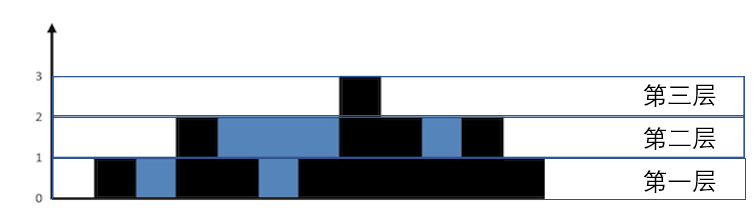
初始left=0，right=11(数组长度)，high=1，high=当前层数。当左右指针指向的区域高度小于high时，左右指针都向中间移动，直到指针指向区域大于等于high的值的时候，指针停下。

第一层：high=1,所以left向右移动到left=1，right保持不动(因为right初始化的区域大于等于high=1)。所以第一层体积为tmp1=right-left+1=11(记得加一奥！)

第二层：high=2，left一直向右移动到left=3，right向左移动到right=10，所以tmp2=right-left+1=8

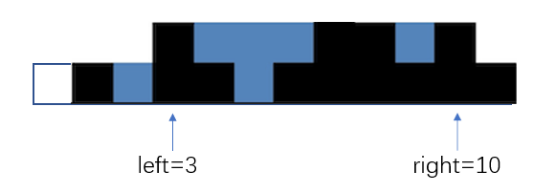
第三层：high=3,left和right向中间移动直至重合，因为重合的时候仍然有体积（所以循环条件里一定要写left<=right,而不是left<right），所以tmp3=right-left+1=1

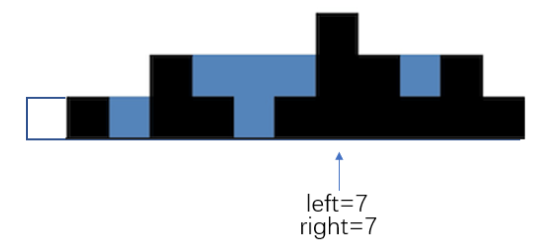
代码

class Solution:
    def trap(self, height):
        n = len(height)
        left, right = 0, n - 1
        SUM, tmp, high = 0, 0, 1
        while (left <= right):
            while (left <= right and height[left] < high):
                SUM += height[left]
                left += 1
            while (right >= left and height[right] < high):
                SUM += height[right]
                right -= 1
            high += 1
            tmp += right - left + 1
        return tmp - SUM

11、正则匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

说明:

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。
示例 1:

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。
示例 2:

输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:

输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。
示例 4:

输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:

输入:
s = "mississippi"
p = "mis*is*p*."
输出: false

class Solution:
    def isMatch(self, sss, ppp):
        # 结束条件
        if not ppp:
            return not sss

        # 匹配第一个字符，后续继续递归匹配
        first_match = (len(sss) > 0) and ppp[0] in {sss[0], '.'}

        # 先处理 `*`
        if len(ppp) >= 2 and ppp[1] == '*':
            # 匹配0个 | 多个
            return self.isMatch(sss, ppp[2:]) or (first_match and self.isMatch(sss[1:], ppp))

        # 处理 `.` ，匹配一个
        return first_match and self.isMatch(sss[1:], ppp[1:])

12、文本左右对齐

给定一个单词数组和一个长度 maxWidth，重新排版单词，使其成为每行恰好有 maxWidth 个字符，且左右两端对齐的文本。

你应该使用“贪心算法”来放置给定的单词；也就是说，尽可能多地往每行中放置单词。必要时可用空格 ' ' 填充，使得每行恰好有 maxWidth 个字符。

要求尽可能均匀分配单词间的空格数量。如果某一行单词间的空格不能均匀分配，则左侧放置的空格数要多于右侧的空格数。

文本的最后一行应为左对齐，且单词之间不插入额外的空格。

说明:

单词是指由非空格字符组成的字符序列。
每个单词的长度大于 0，小于等于 maxWidth。
输入单词数组 words 至少包含一个单词。
示例:

输入:
words = ["This", "is", "an", "example", "of", "text", "justification."]
maxWidth = 16
输出:
[
   "This    is    an",
   "example  of text",
   "justification.  "
]
示例 2:

输入:
words = ["What","must","be","acknowledgment","shall","be"]
maxWidth = 16
输出:
[
  "What   must   be",
  "acknowledgment  ",
  "shall be        "
]
解释: 注意最后一行的格式应为 "shall be    " 而不是 "shall     be",
     因为最后一行应为左对齐，而不是左右两端对齐。       
     第二行同样为左对齐，这是因为这行只包含一个单词。
示例 3:

输入:
words = ["Science","is","what","we","understand","well","enough","to","explain",
         "to","a","computer.","Art","is","everything","else","we","do"]
maxWidth = 20
输出:
[
  "Science  is  what we",
  "understand      well",
  "enough to explain to",
  "a  computer.  Art is",
  "everything  else  we",
  "do                  "
]

"""
将字符串分为三种情况,
1.不为最后一行的情况下,只有一个单词的情况
2.不为最后一行的情况下,有多个单词的情况
3.为最后一行的情况
这里我用currentlength计算每次maxWidth去除掉所需字符串并且每两个字符串去除掉,比如maxWidth=16的时候,取出"This is an"10个字母之后,还剩下6个字母,此时currentlength = 6,
1.不为最后一行的情况下,只有一个单词的情况:
在最后面填补currentlength个空格
2.不为最后一行的情况下,有多个单词的情况
每一行填补的单词数为currentlength//单词的个数
如果遇到多余单词的情况下,每一行<currentlength%单词的个数位置的时候,再补上括号
3.为最后一行的情况下,除了最后一个单词之外,每个单词中间添加一个空格,最后一个单词后面再添加currentlength个空格

注明：
作者：zuo-ni-ai-chi-de-tang-seng-rou
链接：https://leetcode-cn.com/problems/text-justification/solution/li-kou-68xiao-bai-du-neng-kan-dong-de-zi-fu-chuan-/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
"""

class Solution:
    def fullJustify(self, words, maxWidth):
        cur = 0
        results = []
        while cur < len(words):
            # cur为当前words能够达到的末尾单词的数组索引
            begins, currentlength = cur, maxWidth - len(words[cur])
            # begins标记起始下标,cur标记末尾的单词数组下标,currentlength标记去除words[cur]之后的长度
            currentstring = ''
            while cur + 1 < len(words) and currentlength >= len(words[cur + 1]) + 1:
                currentlength = currentlength - (len(words[cur + 1]) + 1)
                cur = cur + 1
            # cur的末尾坐标始终不断地往后移动
            # 只有一个单词并且不为最后一行的时候，当前字符串不断地后续填充空格
            if begins == cur and cur != len(words) - 1:
                currentstring = currentstring + words[cur]
                for i in range(currentlength):
                    currentstring = currentstring + ' '
            # 有多个单词的时候的时候，记录下商和余数
            elif cur != len(words) - 1:
                gap = currentlength // (cur - begins)  # 需要分配的空格
                gap = gap + 1  # 默认单词间的一个空格，因此需要+1
                remains = currentlength % (cur - begins)
                for i in range(begins, cur + 1, 1):
                    currentstring = currentstring + words[i]
                    if i != cur:
                        for j in range(gap):
                            currentstring = currentstring + ' '
                        # 后面添加gap个空格,如果小于remains余数的情况下后面再放置一个空格
                        if i < begins + remains:
                            currentstring = currentstring + ' '
            # 为最后一行时单独考虑
            else:
                for i in range(begins, cur + 1, 1):
                    currentstring = currentstring + words[i]
                    # 最后一行填充字符串,不为最后一个单词的时候再在后面填充一个空格
                    if i != cur:
                        currentstring = currentstring + ' '
                for j in range(currentlength):
                    currentstring = currentstring + ' '
            # 最后一行不足的情况下全部填充空格
            results.append(currentstring)
            cur = cur + 1
        return results

13、双指针-原地算法

给定一组字符，使用原地算法将其压缩。

压缩后的长度必须始终小于或等于原数组长度。

数组的每个元素应该是长度为1 的字符（不是 int 整数类型）。

在完成原地修改输入数组后，返回数组的新长度。

进阶：
你能否仅使用O(1) 空间解决问题？

示例 1：

输入：
["a","a","b","b","c","c","c"]

输出：
返回 6 ，输入数组的前 6 个字符应该是：["a","2","b","2","c","3"]

说明：
"aa" 被 "a2" 替代。"bb" 被 "b2" 替代。"ccc" 被 "c3" 替代。
示例 2：

输入：
["a"]

输出：
返回 1 ，输入数组的前 1 个字符应该是：["a"]

解释：
没有任何字符串被替代。
示例 3：

输入：
["a","b","b","b","b","b","b","b","b","b","b","b","b","a","a"]

输出：
返回 6 ，输入数组的前4个字符应该是：["a","b","1","2","a":"2"]。

解释：
由于第一个字符 "a" 不重复，所以不会被压缩。"bbbbbbbbbbbb" 被 “b12” 替代，但是最后的字符"a"有重复，也要压缩。
注意每个数字在数组中都有它自己的位置。
 

提示：

所有字符都有一个ASCII值在[35, 126]区间内。
1 <= len(chars) <= 1000。

from collections import Counter

class Solution:
    def compress(self, chars: List[str]) -> int:
        if not chars:
            return 0
        elif len(chars) == 1:
            return 1
        
        # 双指针法-原地压缩
        index = 0  # 新字符的下标，由于压缩后的字符串长度一定比之前的短，所以可以使用新的下表然后在原字串上更新
        lens = len(chars)
        i = 0  # 用以统计的指针
        while i < lens:
            j = i + 1  # 用于遍历的指针
            while j < lens and chars[j] == chars[i]:
                j += 1
            if j - i > 1:  # 相同的字符长度大于1，进行压缩：字符+数字
                chars[index] = chars[i]
                index += 1
                strs = str(j-i)
                for s in strs:
                    chars[index] = s
                    index += 1
            else:  # 相同字符的长度等于1，直接写字符，后不加数字
                chars[index] = chars[i]
                index += 1
            i = j
        res = chars[:index]
        print(res)
        return index  # 由于index指向的是压缩后字串的下标，所以可以直接返回index即可

14、双指针滑动窗口

在一排树中，第 i 棵树产生 tree[i] 型的水果。
你可以从你选择的任何树开始，然后重复执行以下步骤：

把这棵树上的水果放进你的篮子里。如果你做不到，就停下来。
移动到当前树右侧的下一棵树。如果右边没有树，就停下来。
请注意，在选择一颗树后，你没有任何选择：你必须执行步骤 1，然后执行步骤 2，然后返回步骤 1，然后执行步骤 2，依此类推，直至停止。

你有两个篮子，每个篮子可以携带任何数量的水果，但你希望每个篮子只携带一种类型的水果。

用这个程序你能收集的水果树的最大总量是多少？

示例 1：

输入：[1,2,1]
输出：3
解释：我们可以收集 [1,2,1]。
示例 2：

输入：[0,1,2,2]
输出：3
解释：我们可以收集 [1,2,2]
如果我们从第一棵树开始，我们将只能收集到 [0, 1]。
示例 3：

输入：[1,2,3,2,2]
输出：4
解释：我们可以收集 [2,3,2,2]
如果我们从第一棵树开始，我们将只能收集到 [1, 2]。
示例 4：

输入：[3,3,3,1,2,1,1,2,3,3,4]
输出：5
解释：我们可以收集 [1,2,1,1,2]
如果我们从第一棵树或第八棵树开始，我们将只能收集到 4 棵水果树。

class Solution:
    """
    用一个指针go向右遍历和一个指向当前水果的指针here
    go用于往右探，here用于指示每一个新的子序列要重前面那个序列里继承哪一位。
    核心是：go往前遍历的时候，如果超过2种水果了，那么go就回退到here的位置重新开始遍历
    """
    def totalFruit(self, tree: List[int]) -> int:
        here, go = 0, 0
        result = 0  # 结果
        lens = len(tree)
        fruitstyles = {}  # 格式为 --> {水果类型: 数量}
        while go < lens:
            # 当前水果类型为2，且tree[go]不在fruitstyles，证明tree[go]是第三种水果
            # 则把go重置到here(第二种水果的初始位置)那里重新遍历
            if len(fruitstyles.keys()) == 2 and tree[go] not in fruitstyles:
                go = here
                fruitstyles = {}
            else:
                fruitstyles[tree[go]] = fruitstyles.get(tree[go], 0) + 1
                here = go if tree[go] != tree[here] else here # 记录下第二种水果的初始位置
                go += 1
            result = max(result, sum(fruitstyles.values()))
        return result

15、数组的相对排序

给你两个数组，arr1 和 arr2，

arr2 中的元素各不相同
arr2 中的每个元素都出现在 arr1 中
对 arr1 中的元素进行排序，使 arr1 中项的相对顺序和 arr2 中的相对顺序相同。未在 arr2 中出现过的元素需要按照升序放在 arr1 的末尾。

示例：

输入：arr1 = [2,3,1,3,2,4,6,7,9,2,19], arr2 = [2,1,4,3,9,6]
输出：[2,2,2,1,4,3,3,9,6,7,19]
 

提示：

arr1.length, arr2.length <= 1000
0 <= arr1[i], arr2[i] <= 1000
arr2 中的元素 arr2[i] 各不相同
arr2 中的每个元素 arr2[i] 都出现在 arr1 中

from collections import defaultdict


class Solution:
    def relativeSortArray(self, arr1: List[int], arr2: List[int]) -> List[int]:
        result = []
        notexists = []
        tmp_dic = defaultdict(int)
        for i in arr1:
            if i not in arr2:
                notexists.append(i)
            else:
                tmp_dic[i] += 1

        for j in arr2:
            result.extend([j]*tmp_dic[j])
        notexists.sort()
        result.extend(notexists)
        return result

方法2

class Solution:
    def relativeSortArray(self, arr1: List[int], arr2: List[int]) -> List[int]:
        notexists = []
        exits = []
        for i in arr1:
            if i not in arr2:
                notexists.append(i)
            else:
                exits.append(i)

        exits.sort(key=lambda x: arr2.index(x))
        notexists.sort()
        result = exits + notexists
        return result

16、自定义字符串排序

字符串S和 T 只包含小写字符。在S中，所有字符只会出现一次。

S 已经根据某种规则进行了排序。我们要根据S中的字符顺序对T进行排序。更具体地说，如果S中x在y之前出现，那么返回的字符串中x也应出现在y之前。

返回任意一种符合条件的字符串T。

示例:
输入:
S = "cba"
T = "abcd"
输出: "cbad"
解释:
S中出现了字符 "a", "b", "c", 所以 "a", "b", "c" 的顺序应该是 "c", "b", "a".
由于 "d" 没有在S中出现, 它可以放在T的任意位置. "dcba", "cdba", "cbda" 都是合法的输出。
注意:

S的最大长度为26，其中没有重复的字符。
T的最大长度为200。
S和T只包含小写字符。

from collections import Counter 

class Solution:
    def customSortString(self, S: str, T: str) -> str:
        exists = Counter(T)
        notexists = ""
        result = ""
        for i in T:
            if i not in S:
                notexists += i

        for j in S:
            if j in exists:
                tmp = j * exists[j]
                result += tmp
        result = result + notexists
        return result