矩阵快速幂
---!x^n+y^n=z^n
定义矩阵A(m*n),B(p*q),A*B有意义当且仅当n=p。即A的列数等于B的行数。
且C=A*B,C(m*q)。
例如:

进入正题,由于现在全国卷高考不考矩阵,也没多大了解。因为遇到了斐波那契这题...
注意到: Fn+1=Fn+Fn-1
我们会有:
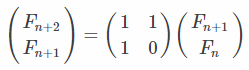
则:
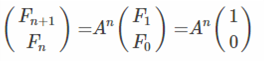
所以我们只需要想办法求矩阵A的幂,这时候我们当然想要用快速幂。
代码部分:
定义矩阵:
struct matrix{ ll a[3][3]; };
(类比整数的快速幂)预处理:
[我们需要一类似于1的矩阵:]
『1 0 0
0 1 0
0 0 1』类似这种操作...
void init(){ int i,j; memset(res.a,0,sizeof res.a); for(i=1;i<=2;i++) res.a[i][i]=1; base.a[1][1]=1; base.a[1][2]=1; base.a[2][1]=1; base.a[2][2]=0;
}
矩阵乘法:[就该题而言]
matrix mul(matrix p,matrix q){ int i,j,k; matrix m; memset(m.a,0,sizeof m.a); for(i=1;i<=2;i++) for(j=1;j<=2;j++) for(k=1;k<=2;k++) m.a[i][j]=(m.a[i][j]+p.a[i][k]*q.a[k][j])%Mod; return m; }
快速幂:
void mfpow(ll p){ init(); while(p){ if(p&1) res=mul(base,res); base=mul(base,base); p>>=1; } }
全部的代码:(lowbee的难免会差一些,请大佬们见谅...)
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 typedef long long ll ; 6 inline ll read(); 7 const ll Mod = 1e9 + 7 ; 8 struct matrix{ 9 ll a[3][3]; 10 }; 11 matrix res,base; 12 ll ans; 13 ll c[3]; 14 ll n; 15 namespace lys{ 16 void init(){ 17 int i,j; 18 memset(res.a,0,sizeof res.a); 19 for(i=1;i<=2;i++) res.a[i][i]=1; 20 base.a[1][1]=1; 21 base.a[1][2]=1; 22 base.a[2][1]=1; 23 base.a[2][2]=0; 24 } 25 matrix mul(matrix p,matrix q){ 26 int i,j,k; 27 matrix m; 28 memset(m.a,0,sizeof m.a); 29 for(i=1;i<=2;i++) 30 for(j=1;j<=2;j++) 31 for(k=1;k<=2;k++) 32 m.a[i][j]=(m.a[i][j]+p.a[i][k]*q.a[k][j])%Mod; 33 return m; 34 } 35 void mfpow(ll p){ 36 init(); 37 while(p){ 38 if(p&1) res=mul(base,res); 39 base=mul(base,base); 40 p>>=1; 41 } 42 } 43 int main(){ 44 int k; 45 n=read(); 46 mfpow(n-1); 47 c[1]=1; 48 c[2]=0; 49 for(k=1;k<=2;k++) 50 ans=(ans+res.a[1][k]*c[k])%Mod; 51 cout<<ans<<endl; 52 return 0; 53 } 54 } 55 int main(){ 56 lys::main(); 57 return 0; 58 } 59 inline ll read(){ 60 ll k=0,f=1; 61 char c=getchar(); 62 while(c<'0'||c>'9'){ 63 if(c=='-') 64 f=-1; 65 c=getchar(); 66 } 67 while(c>='0'&&c<='9'){ 68 k=k*10+c-'0'; 69 c=getchar(); 70 } 71 return k*f; 72 }
题目链接[luogu]:
https://www.luogu.org/problem/show?pid=1962