解题代码部分来自网友,如果有不对的地方,欢迎各位大佬评论
题目1、海盗分金币有5个海盗,相约进行一次帆船比赛。
比赛中天气发生突变,他们被冲散了。
恰巧,他们都先后经过途中的一个无名的荒岛,并且每个人都信心满满,觉得自己是第一个经过该岛的人。
第一个人在沙滩上发现了一堆金币。他把金币分成5等份。发现刚好少一个金币。他就从自己口袋拿出一个金币补充进去,然后把属于自己的那份拿走。
第二个到达的人也看到了金币,他也和第一个人一样,把所有金币5等分,发现刚好缺少一个金币,于是自己补进去一个,拿走了属于自己的那份。
第三,第四,第五人的情况一模一样。
等他们到了目的地,都说自己的情况,才恍然大悟,一起去荒岛找金币,然而再也没有找到荒岛。他们都惋惜地说:岛上还有一千多枚金币呢!
请你根据这些信息,推算荒岛上最初有多少金币?
这是一个整数,请通过浏览器提交答案,不要填写任何多余的内容(比如说明性的文字等)
3129public class Main {
public static void main(String[] args) {
for(int i = 1000;i < 100000;i++) {
int a1, a2, a3, a4, a5;
if((i + 1) % 5 != 0)
continue;
a1 = (i + 1) / 5 - 1;
if((i - a1 + 1) % 5 != 0)
continue;
a2 = (i - a1 + 1) / 5 - 1;
if((i - a1 - a2 + 1) % 5 != 0)
continue;
a3 = (i - a1 - a2 + 1) / 5 - 1;
if((i - a1 - a2 - a3 + 1) % 5 != 0)
continue;
a4 = (i - a1 - a2 - a3 + 1) / 5 - 1;
if((i - a1 - a2 - a3 - a4 + 1) % 5 != 0)
continue;
a5 = (i - a1 - a2 - a3 - a4 + 1) / 5 - 1;
int temp = i - a1 - a2 - a3 - a4 - a5;
if(temp > 1000 && temp < 2000)
System.out.println("i = "+i);
}
}
}
里面的*在编写的时候会自动编译成线,这里就用代码的格式把题目弄过来
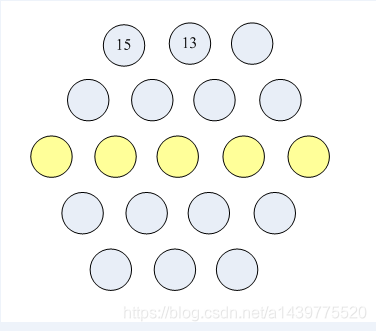
把 1 2 3 ... 19 共19个整数排列成六角形状,如下:
* * *
* * * *
* * * * *
* * * *
* * *
要求每个直线上的数字之和必须相等。共有15条直线哦!
再给点线索吧!我们预先填好了2个数字,第一行的头两个数字是:15 13,参见图【p1.png】,黄色一行为所求。
请你填写出中间一行的5个数字。数字间用空格分开。
这是一行用空格分开的整数,请通过浏览器提交答案,不要填写任何多余的内容(比如说明性的文字等)
public class Main {
public static boolean[] used = new boolean[20];
public void swap(int[] A, int i, int j) {
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
public boolean check(int[] A, int step) {
int sum = A[0] + A[1] + A[2];
if(step >= 7) {
if(A[3] + A[4] + A[5] + A[6] != sum)
return false;
}
if(step >= 8)
if(A[0] + A[3] + A[7] != sum)
return false;
if(step >= 12) {
if(A[7] + A[8] + A[9] + A[10] + A[11] != sum)
return false;
if(A[2] + A[6] + A[11] != sum)
return false;
}
if(step >= 13)
if(A[1] + A[4] + A[8] + A[12] != sum)
return false;
if(step >= 16) {
if(A[12] + A[13] + A[14] + A[15] != sum)
return false;
if(A[1] + A[5] + A[10] + A[15] != sum)
return false;
}
if(step >= 17) {
if(A[2] + A[5] + A[9] + A[13] + A[16] != sum || A[7]+A[12]+A[16] != sum)
return false;
}
if(step >= 18)
if(A[3] + A[8] + A[13] + A[17] != sum || A[6] + A[10] + A[14] + A[17] != sum)
return false;
if(step >= 19) {
if(A[0]+A[4]+A[9]+A[14]+A[18] != sum || A[16] + A[17] + A[18] != sum || A[11] + A[15] + A[18] != sum)
return false;
}
return true;
}
public void dfs(int[] A, int step) {
if(check(A, step) == false)
return;
if(step == 19) {
for(int i = 0;i < A.length;i++)
System.out.print(A[i]+" ");
System.out.println();
return;
}
for(int i = 1;i <= 19;i++) {
if(used[i] == false) {
used[i] = true;
A[step] = i;
dfs(A, step + 1);
used[i] = false;
}
}
}
public static void main(String[] args) {
Main test = new Main();
int[] A = new int[19];
A[0] = 15;
A[1] = 13;
A[2] = 10;
used[15] = true;
used[13] = true;
used[10] = true;
test.dfs(A, 3);
}
}
X星球的母鸡很聪明。它们把蛋直接下在一个 N * N 的格子中,每个格子只能容纳一枚鸡蛋。它们有个习惯,要求:每行,每列,以及每个斜线上都不能有超过2个鸡蛋。如果要满足这些要求,母鸡最多能下多少蛋呢,有多少种摆放方法呢?
下面的程序解决了这个问题,请仔细分析程序逻辑,推断划线处缺少的代码。
public class A
{
static int max = 0;
static int T = 0;
static final int N = 6;
// 只能在(r,c) 以及其右,其下放置
static void f(int[][] da, int r, int c)
{
if(r>=N){
int n = count(da);
if(n>max) {
max = n;
T = 0;
}
if(n==max) T++;
return;
}
//计算一下步放哪
int r_next = r;
int c_next = c + 1;
if(c_next>=N){
c_next = 0;
r_next++;
}
if(____________________){ // 填空位置
da[r][c] = 1;
f(da, r_next, c_next);
}
da[r][c] = 0;
f(da, r_next, c_next);
}
static int count(int[][] da)
{
int n = 0;
for(int i=0; i<da.length; i++)
for(int j=0; j<da[i].length; j++)
if(da[i][j]==1) n++;
return n;
}
static int spy(int[][] da, int r, int c)
{
int m=0;
// 该行
int n=0;
for(int i=0; i<N; i++) if(da[r][i]==1) n++;
if(n>m) m = n;
//该列
n=0;
for(int i=0; i<N; i++) if(da[i][c]==1) n++;
if(n>m) m = n;
//右斜线
n=0;
for(int i=0; i<N; i++){
if(r-i<0 || c-i<0) break;
if(da[r-i][c-i]==1) n++;
}
for(int i=1; i<N; i++){
if(r+i>=N || c+i>=N) break;
if(da[r+i][c+i]==1) n++;
}
if(n>m) m = n;
//左斜线
n=0;
for(int i=0; i<N; i++){
if(r-i<0 || c+i>=N) break;
if(da[r-i][c+i]==1) n++;
}
for(int i=1; i<N; i++){
if(r+i>=N || c-i<0) break;
if(da[r+i][c-i]==1) n++;
}
if(n > m) m = n;
return m;
}
public static void main(String[] args)
{
int[][] da = new int[N][N];
f(da, 0, 0);
System.out.println(max);
System.out.println(T);
}
}
注意:通过浏览器提交答案。只填写缺少的内容,不要填写任何多余的内容(例如:说明性文字或已有符号)。
spy(da, r, c) < 2
如果用a b c d这4个字母组成一个串,有4!=24种,如果把它们排个序,每个串都对应一个序号:
abcd 0
abdc 1
acbd 2
acdb 3
adbc 4
adcb 5
bacd 6
badc 7
bcad 8
bcda 9
bdac 10
bdca 11
cabd 12
cadb 13
cbad 14
cbda 15
cdab 16
cdba 17
…
现在有不多于10个两两不同的小写字母,给出它们组成的串,你能求出该串在所有排列中的序号吗?
【输入格式】
一行,一个串。
【输出格式】
一行,一个整数,表示该串在其字母所有排列生成的串中的序号。注意:最小的序号是0。
例如:
输入:
bdca
程序应该输出:
11
再例如:
输入:
cedab
程序应该输出:
70
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static char[] arrayA;
//返回n!= 1*2*3*...*n
public long getN(int n) {
long result = 1;
for(int i = 1;i <= n;i++)
result = result * i;
return result;
}
public void getResult(String A) {
int len = A.length();
arrayA = A.toCharArray();
Arrays.sort(arrayA);
boolean[] used = new boolean[len];
long count = 0;
for(int i = 0;i < len;i++) {
char t = A.charAt(i);
int a = 0;
for(int j = 0;j < len;j++) {
if(used[j] == true)
continue;
if(arrayA[j] == t) {
used[j] = true;
break;
}
a++;
}
count = count + a * getN(len - 1 - i);
}
System.out.println(count);
}
public static void main(String[] args) {
Main test = new Main();
Scanner in = new Scanner(System.in);
String A = in.next();
test.getResult(A);
}
}
天才少年的邻居 atm 最近学习了线性代数相关的理论,他对“矩阵”这个概念特别感兴趣。矩阵中有个概念叫做幂零矩阵。对于一个方阵 M ,如果存在一个正整数 k 满足 M^k = 0 ,那么 M 就是一个幂零矩阵。(^ 表示乘方)
atm 不满足幂零矩阵,他自己设想了一个幂一矩阵:对于一个方阵 M ,如果存在一个正整数 k 满足 M^k = I ,其中 I 是单位矩阵,那么 M 就是一个幂一矩阵。
atm 特别钟情于这样一种方阵:每行每列有且仅有一个 1 。经过 atm 不断实验,他发现这种矩阵都是幂一矩阵。
现在,他的问题是,给定一个满足以上条件的方阵,他想求最小的 k 是多少。
【输入格式】
第一行一个正整数 n ,表示矩阵大小是 n * n 。
接下来 n 行,每行两个正整数 i j 表示方阵的第 i 行第 j 列为 1。
1 <= i, j <= n 。
行号,列号都从1开始。
【输出格式】
一行。一个正整数,即题目中所说最小的 k 。
【样例输入】
5
3 1
1 2
4 4
2 3
5 5
【样例输出】
3
【数据范围】
对于 30% 的数据满足 n <= 10
对于 60% 的数据答案不超过 10^18
对于 100% 的数据满足 n <= 10000
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
import java.util.Scanner;
public class 第五题 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
//创建索引数组num[n]
int[] num = new int[n];
for(int i = 0;i<n;i++){
//输入数组,注意要-1,因为题目说输入的行和列都是以1开始
num[in.nextInt()-1] = in.nextInt()-1;
}
//这里vis数组为了加快循环
boolean[] vis = new boolean[n];
//max存储最终结果
long max = 1;
//从原数组的第0行开始,寻找搜索
for(int i = 0;i<n;i++){
//如果当前行已经被搜索过,直接continue
if(vis[i]){
continue;
}
//count记录搜索次数(题目说对于 60% 的数据答案不超过 10^18 ,这里以防万一,用long)
long count = 1;
//s为每次搜索的数组下标索引
int s = i;
//当前第s行被搜索了,记录vis数组
vis[s] = true;
//当索引与值不相等时就继续循环
while(num[s] != i){
//每次循环一次count+1
count++;
//当前索引对应的值是下一次的索引
s = num[s];
//当前索引对应的行被搜索过,记录vis数组
vis[s] = true;
}
//搜索结束,判断搜索结果是否能被max整除
if(max%count!=0){
//计算max和count的最小公倍数存入max
if(max>count){
max = max*count/gcd(max,count);
}else{
max = max*count/gcd(count,max);
}
}
}
//输出最终结果
System.out.println(max);
in.close();
}
private static long gcd(long max, long count) {
//辗转相除法求最大公约数
if(max%count==0){
return count;
}
return gcd(count,max%count);
}
}
X星球的居民点很多。Pear决定修建一个浩大的水利工程,以解决他管辖的N个居民点的供水问题。现在一共有N个水塔,同时也有N个居民点,居民点在北侧从1号到N号自西向东排成一排;水塔在南侧也从1号到N号自西向东排成一排。
N条单向输水线(有水泵动力),将水从南侧的水塔引到北侧对应的居民点。
我们不妨将居民点和水塔都看做平面上的点,居民点坐标为(1,K)(N,K),水塔为(1,0)(N,0)。
除了N条纵向输水线以外,还有M条单向的横向输水线,连接(Xi,Yi)和(Xi,(Yi)+1)或者(Xi,Yi)和(Xi,(Yi)-1)。前者被称为向右的水路,而后者是向左的。不会有两条水路重叠,即便它们方向不同。
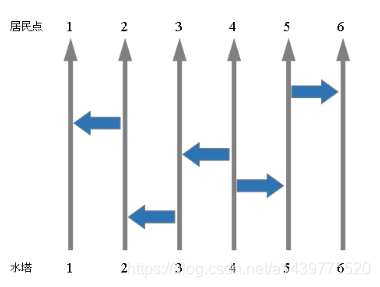
布局的示意图如:【p1.png】所示。
显然,每个水塔的水都可以到达若干个居民点(而不仅仅是对应的那个)。例如上图中,4号水塔可以到达3、4、5、6四个居民点。
现在Pear决定在此基础上,再修建一条横向单项输水线。为了方便考虑,Pear认为这条水路应当是自左向右的,也就是连接了一个点和它右侧的点(例如上图中连接5和6两个纵线的横向水路)。
Pear的目标是,修建了这条水路之后,能有尽可能多对水塔和居民点之间能到达。换句话说,设修建之后第i个水塔能到达Ai个点,你要最大化A1+A2+…+An。
根据定义,这条路必须和X轴平行,但Y坐标不一定要是整数。注意:虽然输入中没有重叠的水路,但是你的方案可以将新修的输水线路与已有的水路重叠。
【输入数据】
输入第一行包含三个正整数N,M,K,含义如题面所述:N是纵向线数,M横向线数,K是居民点纵坐标。
接下来M行,每行三个整数。前两个正整数Xi Yi表示水路的起点坐标;
1<=Xi<=N,0<Yi<K。
接下来一个数0或者1,如果是0表示这条水路向左,否则向右。
保证水路都是合法的,也就是不会流向没有定义的地方。
【输出数据】
输出一行。是一个正整数,即:题目中要求的最大化的A1+A2+…+An。
【输入样例1】
4 3 2
1 1 1
3 1 0
3 1 1
【输出样例1】
11
【输入样例2】
7 9 4
2 3 0
7 2 0
6 3 1
6 1 0
2 1 1
3 3 1
5 2 0
2 2 1
7 1 0
【输出样例2】
21
【数据范围】
对于20%的数据,N,K<=20,M<=100
对于40%的数据,N,K<=100,M<=1000
对于60%的数据,N,K<=1000,M<=100000
对于100%的数据,N,K<=50000,M<=100000
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 5000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
import java.util.Scanner;
public class Main {
public static int n, m , k;
public static int[][] value;
public void getResult() {
int max = Integer.MIN_VALUE;
for(int i = 1;i < n;i++) {
if(value[i][i+1] == 0) {
value[i][i+1] = 1;
int temp = 0;
for(int k = 1;k <= n;k++) {
temp++;
int t = k - 1;
while(t >= 1) { //寻找左边连通水磊
if(value[t][t+1] == 1) {
temp++;
t--;
} else
break;
}
t = k + 1;
while(t <= n) { //寻找右边连通水磊
if(value[t][t-1] == 1) {
temp++;
t++;
} else
break;
}
}
max = Math.max(max, temp);
value[i][i+1] = 0;
}
}
System.out.println(max);
}
public static void main(String[] args) {
Main test = new Main();
Scanner in = new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
k = in.nextInt();
value = new int[n + 1][n + 1];
for(int i = 0;i < m;i++) {
int x = in.nextInt();
@SuppressWarnings("unused")
double y = in.nextDouble();
int c = in.nextInt();
if(c == 0)
value[x][x - 1] = 1; //单向向左连通
else
value[x][x + 1] = 1; //单向向右连通
}
test.getResult();
}
}