扩展欧几里德算法

    扩展欧几里德算法

   扩展欧几里德算法是用来在已知a, b求解一组x，y [x,y都是整数]，使它们满足贝祖等式： ax+by = gcd(a, b) =d（解一定存在，根据数论中的相关定理）。扩展欧几里德常用在求解模线性方程及方程组中。

   证明

    当 b=0 gcd（a，b）=a。此时 x=1，y=0；

      ax+by = gcd(a, b);

      bx1+a%by1=gcd(b, a%b);

     根据 gcd(a, b) = gcd (b, a%b);

     ax+by  =  bx1+a%by1;

     a%b = (a- (a/b)*b)

     ax+ by = ay1+ b(x1-(a/b)*by1);

     x=y1; y= x1- a/b*by1;

    这样我们就得到了求解 x, y 的方法：x，y 的值基于 x1，y1.

　 上面的思想是以递归定义的，因为 gcd 不断的递归求解一定会有个时候 b=0，所以递归可以结束。

    代码

int exgcd(int a, int b, int &x, int &y) {//x, y表示解 
  if (b == 0) {
    x = 1;
    y = 0;
    return a;
  }
  int k = exgcd(b, a%b, x, y);
  int t=x;
  x=y;
  y=t-(a/b)*y;
  return k;
}

   拓展欧几里得的几个应用

   1求解不定方程； 

   例如：求解不定整数方程ax+by = c

     求ax+by = c， 令d =gcd(a,b);

     那么(a / d ) * x + (b / d )* y = c / d

     因为(a / d )、(b / d ) 、x、y都是整数，那么保证原不定整数方程ax+by = c有解的充要条件就是c / d为整数，即c是gcd(a,b)的倍数。

    如果有解，那么令 K = c/d；

    那么，对方程aX+bY = d；假设有拓展欧几里得求出一组解为(X0,Y0)，那么aX0+bY0 = d；等式两边同时乘以K，即K*( aX0+bY0 ) = d*K = c；由恒等关系，原方程的解（x0，y0）：

    X0 = KX0 = c/d * X0，y0 = KY0 = c/d *Y0。

      不定方程的通解：

       若（x0，y0）是不定整数方程ax+by = c的一组解，则他的任意整数解都可以表示成（x0+ kb’, y0-ka’），其中a’ = a/gcd(a,b), b’ = b/gcd(a,b).

       题目  nyoj1235

        

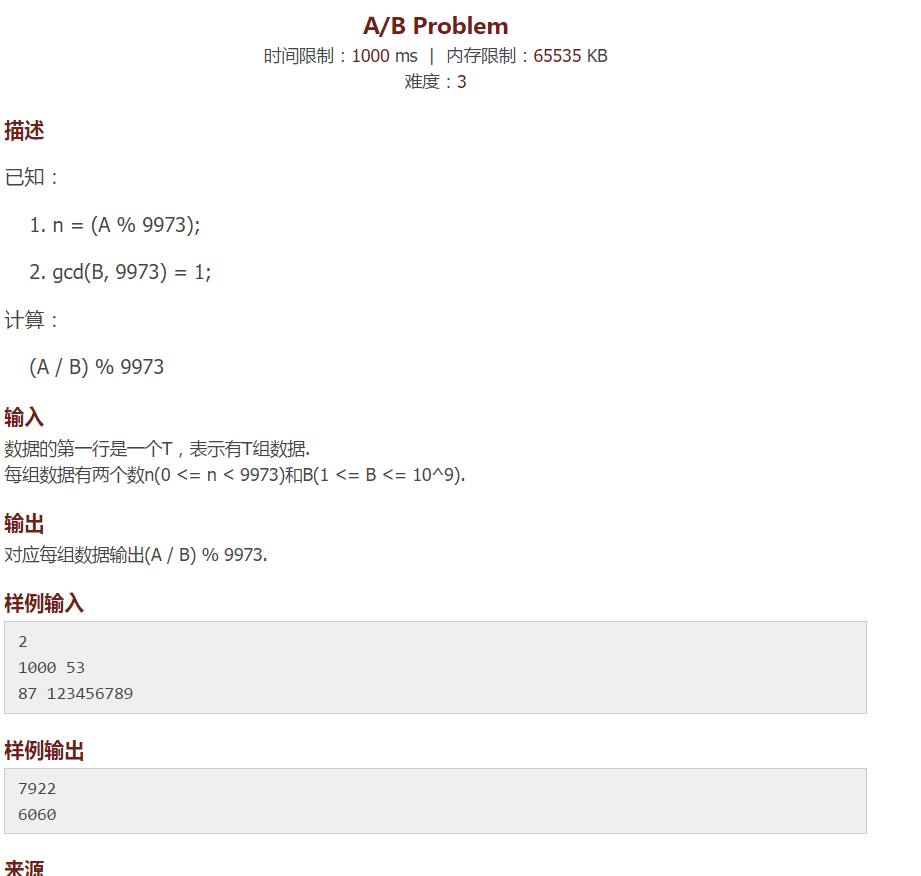
       a/b%m=k//设等于k

       a/b=k + xm

        a=kb+xmb

       a%m=kb%m+0

      n = kb%m;

      bx+my=gcd(b, m)=1;

      xb%m+my%m=n;

      x=k;

     xb/n%m+my/n%m=1;

    把x/m%m, y.n%m 看成一个整体

     解得 x=k/n;

     k=x*n;

   2求解模线性方程（线性同余方程）；

  .......

   3求解模的逆元；

.....