递归的定义
在定义一个过程或函数时,出现直接或者间接调用自己的成分,称之为递归。
若直接调用自己,称之为直接递归;若间接调用自己,称之为间接递归。
如果一个递归函数中递归调用语句是最后一条执行语句,则称这种递归调用为尾递归。
尾递归算法:可以用循环语句转换为等价的非递归算法
其他递归算法:可以通过栈来转换为等价的非递归算法
使用递归的场景
(1)定义是递归的
有许多数学公式、数列等的定义是递归的。例如,求n!和Fibonacci数列等。这些问题的求解过程可以将其递归定义直接转化为对应的递归算法。
(2)数据结构是递归的
有些数据结构是递归的。 例如, 单链表就是一种递归数据结构, 其节点类型定义如下:
1 typedef struct LNode 2 { 3 ElemType data; 4 struct LNode *next; //指向同类型节点的指针 5 } LinkList;
不带头节点单链表示意图:
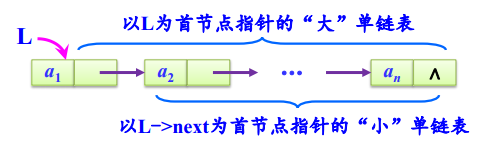
(3)问题的求解方法是递归的

递归模型
一个递归模型是由递归出口和递归体两部分组成。
递归出口确定递归到何时结束;递归体确定递归求解时的递推关系。
f(sn) = g(f(si), f(si+1), …, f(sn-1), cj, cj+1, …, cm)
其中g是一个非递归函数,c是常量。
把一个不能或不好直接求解的“大问题”转化成一个或几个“小问题”来解决; 再把这些“小问题”进一步分解成更小的“小问题” 来解决。 直到每个“小问题”都可以直接解决(此时分解到递归出口)。
但递归分解不是随意的分解,递归分解要保证“大问题”与“小问题”相似,即求解过程与环境都相似。
f(s1) = m1
f(sn) = g(f(sn-1), cn-1)
求f(sn)的分解过程如下:
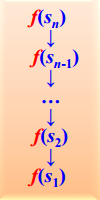
遇到递归出口发生“质变” , 即原递归问题便转化成可以直接求解的问题。 求值过程:

这样f(sn)便计算出来了,因此递归的执行过程由分解和求值两部分构成。
求递归模型的步骤
(1)对原问题f(s)进行分析, 称为“ 大问题” ,假设出合理的“ 小问题” f(s’)
(2)假设f(s’)是可解的, 在此基础上确定f(s)的解, 即给出f(s)与f(s’)之间的关系,即递归体
(3)确定一个特定情况(如f(1)或f(0))的解,即递归出口
应用
1、采用递归算法求实数数组A[0..n-1]中的最小值
分析:

假设f(A,i-1)已求出, 则f(A,i)=MIN(f(A,i-1), A[i]), 其中MIN()为求两个值较小值函数。
当i=0时,只有一个元素,有f(A,i)=A[0]。
递归模型:
f(A,i) = A[0] 当i=0时
f(A,i) = MIN(f(A,i-1), A[i]) 其他情况
代码:
1 float f(float A[], int i) 2 { 3 float m; 4 if (i == 0) 5 return A[0]; 6 else 7 { 8 m = f(A, i - 1); 9 10 if (m > A[i]) 11 return A[i]; 12 else 13 return m; 14 } 15 }
2、求单链表中数据节点个数
分析:
空单链表的数据节点个数为0,即 f(L)=0 当L=NULL
对于非空单链表:
考虑一下我们的链表模型:

则可以得出下面的图:

递归模型:
f(L) = 0 当L=NULL
f(L) = f(L->next) + 1 其他情况
代码:
1 int count(Node *L) 2 { 3 if (L == NULL) 4 return 0; 5 else 6 return count(L->next) + 1; 7 }
3、正向显示所有节点值
分析:
假设f(L->next)已求解
f(L)等价于输出L->data; f(L->next);
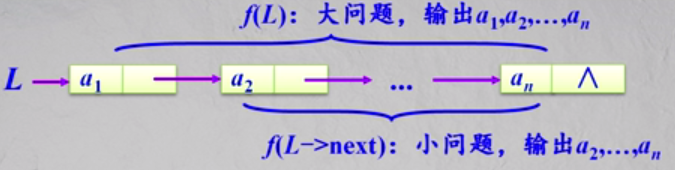
递归模型:
f(L) 不做任何事件 当L=NULL
f(L) 输出L->data;f(L->next) 其他情况
代码:
1 void traverse(Node *L) 2 { 3 if (L == NULL) 4 return; 5 6 printf("%d ", L->data); 7 traverse(L->next); 8 }
4、反向显示所有节点值
分析:
假设f(L->next)已求解
f(L)等价于f(L->next);输出L->data;
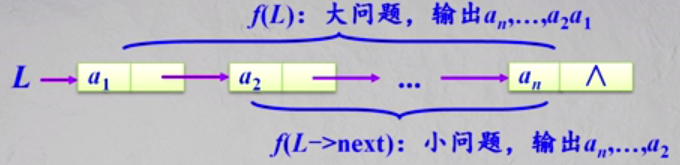
递归模型:
f(L) 不做任何事件 当L=NULL
f(L) f(L->next);输出L->data 其他情况
代码:
1 void traverseR(Node *L) 2 { 3 if (L == NULL) 4 return; 5 6 traverseR(L->next); 7 printf("%d ", L->data); 8 }
5、采用递归算法求解迷宫问题,并输出从入口到出口的所有迷宫路径
分析:
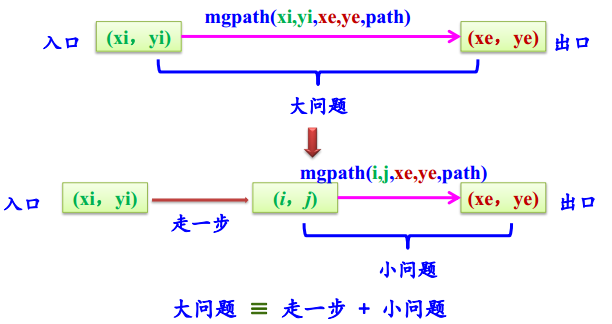
递归模型:
mgpath(xi,yi,xe,ye,path) 将(xi,yi)添加到path中;输出path中的迷宫路径; 若(xi,yi)=(xe,ye)
mgpath(xi,yi,xe,ye,path) 对于(xi,yi)四周的每一个相邻方块(i,j):
(1)将(xi,yi)添加到path中;
(2)置mg[xi][yi]=-1;
(3)mgpath(i,j,xe,ye,path);
(4)path回退一步并置mg[xi][yi]=0; (在一个“小问题” 执行完后回退是为了找所有解)
若(xi,yi)不为出口且可走
代码:
1 typedef struct 2 { 3 int i; //当前方块的行号 4 int j; //当前方块的列号 5 } Box; 6 7 typedef struct 8 { 9 Box data[MaxSize]; 10 int length; //路径长度 11 } PathType; //定义路径类型 12 13 int mg[M+2][N+2] = //M=4, N=4 14 { 15 {1, 1, 1, 1, 1, 1}, 16 {1, 0, 0, 0, 1, 1}, 17 {1, 0, 1, 0, 0, 1}, 18 {1, 0, 0, 0, 1 ,1}, 19 {1, 1, 0, 0, 0, 1}, 20 {1, 1, 1, 1, 1, 1} 21 }; 22 23 void mgpath(int xi,int yi,int xe,int ye,PathType path) 24 //求解路径为:(xi,yi) (xe,ye) 25 { 26 int di,k,i,j; 27 if (xi == xe && yi == ye) 28 { 29 path.data[path.length].i = xi; 30 path.data[path.length].j = yi; 31 path.length++; 32 printf("迷宫路径%d如下: ",++count); 33 34 for (k = 0; k < path.length; k++) 35 { 36 printf(" (%d, %d)", path.data[k].i, path.data[k].j); 37 38 if ((k + 1) % 5 == 0) //每输出每5个方块后换一行 39 printf(" "); 40 } 41 printf(" "); 42 } 43 else //(xi,yi)不是出口 44 { 45 if (mg[xi][yi] == 0) //(xi,yi)是一个可走方块 46 { 47 di= 0; 48 while (di<4) //对于(xi,yi)四周的每一个相邻方位di 49 { 50 switch(di) //找方位di对应的方块(i,j) 51 { 52 case 0: 53 i = xi-1; j = yi; break; 54 case 1: 55 i = xi; j = yi + 1; break; 56 case 2: 57 i = xi + 1; j = yi; break; 58 case 3: 59 i = xi; j = yi - 1; break; 60 } 61 path.data[path.length].i = xi; 62 path.data[path.length].j = yi; 63 path.length++; //路径长度增1 64 mg[xi][yi]=-1; //避免来回重复找路径 65 66 mgpath(i,j,xe,ye,path); 67
68 path.length--; //回退一个方块 69 mg[xi][yi]=0; //恢复(xi,yi)为可走 70 di++; 71 } //-while 72 } //- if (mg[xi][yi]==0) 73 } //-递归体 74 } 75 76 int main() 77 { 78 PathType path; 79 path.length=0; 80 81 mgpath(1, 1, 4, 4, path); 82 83 return 0; 84 }
初始:
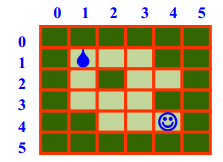
结果:
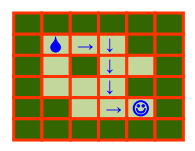
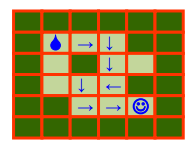
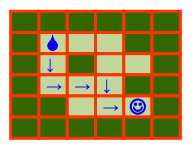

本文图片参考自:配套ppt课件