优先搜索(DFS, Depth First Search)是一个针对图和树的遍历算法。早在19世纪就被用于解决迷宫问题。
对于下面的树而言,DFS方法首先从根节点1开始,其搜索节点顺序是1,2,3,4,5,6,7,8(假定左分枝和右分枝中优先选择左分枝)。
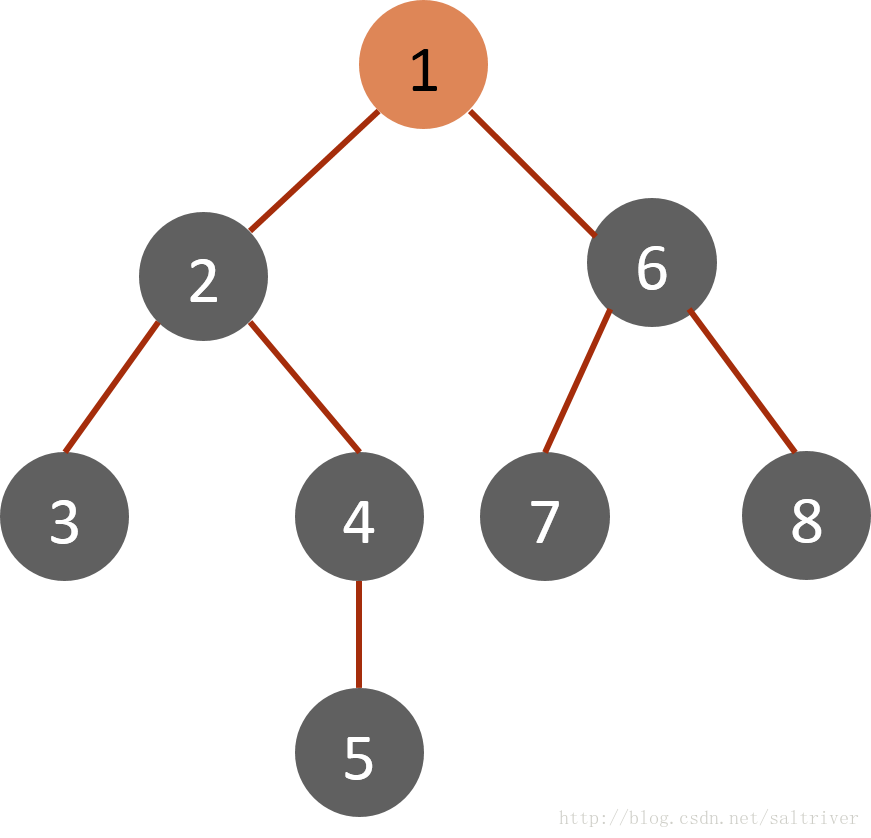
DFS的实现方式相比于BFS应该说大同小异,只是把queue换成了stack而已,stack具有后进先出LIFO(Last Input First Output)的特性,
DFS的操作步骤如下:
1、把起始点放入stack;
2、重复下述3步骤,直到stack为空为止:
a、从stack中访问栈顶的点;
b、找出与此点邻接的且尚未遍历的点,进行标记,然后全部放入stack中;
c、如果此点没有尚未遍历的邻接点,则将此点从stack中弹出。
下面结合一个图(graph)的实例,说明DFS的工作过程和原理:
(1)将起始节点1放入栈stack中,标记为已遍历。
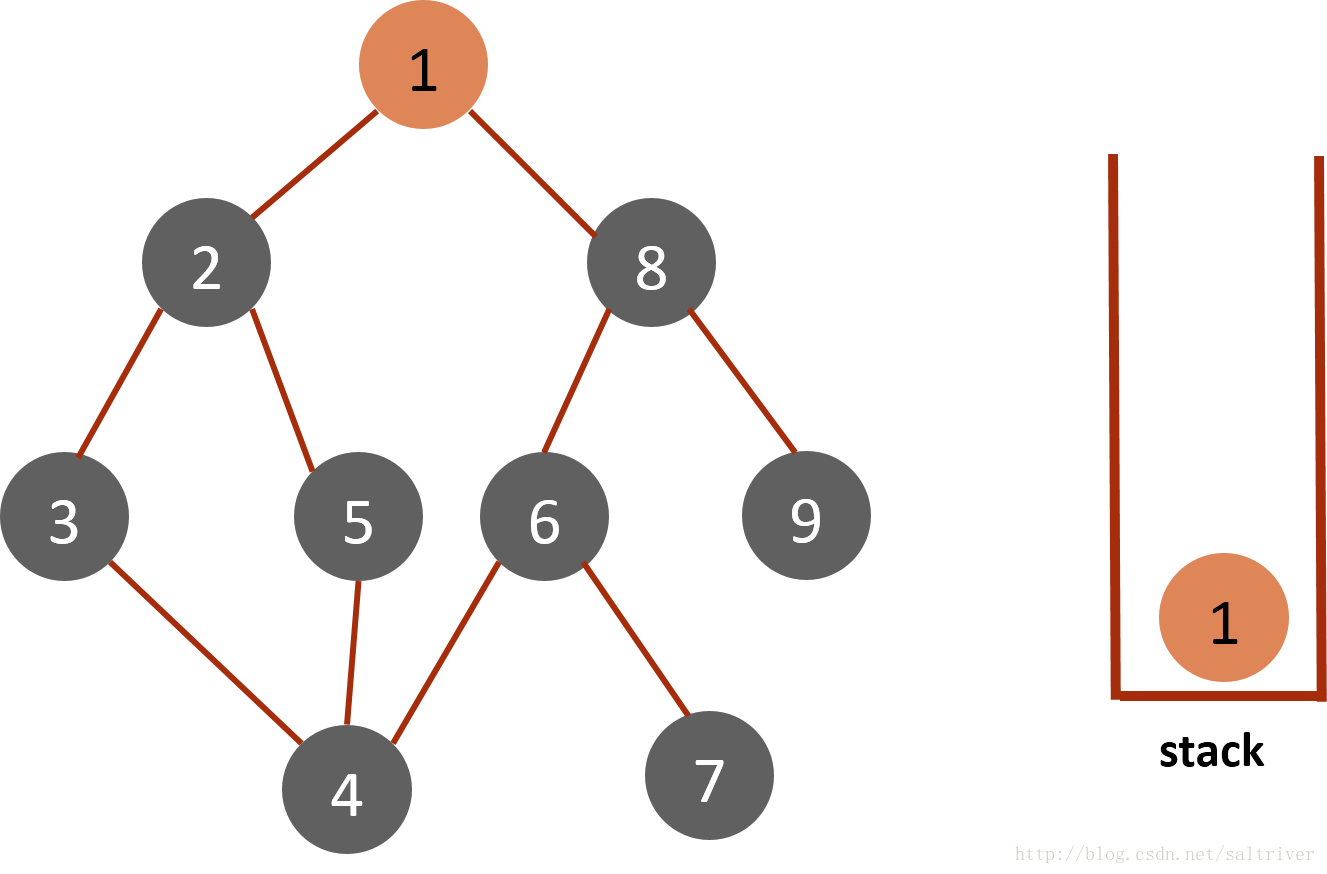
(2)从stack中访问栈顶的节点1,找出与节点1邻接的节点,有2,9两个节点,我们可以选择其中任何一个,选择规则可以人为设定,这里假设按照节点数字顺序由小到大选择,选中的是2,标记为已遍历,然后放入stack中。
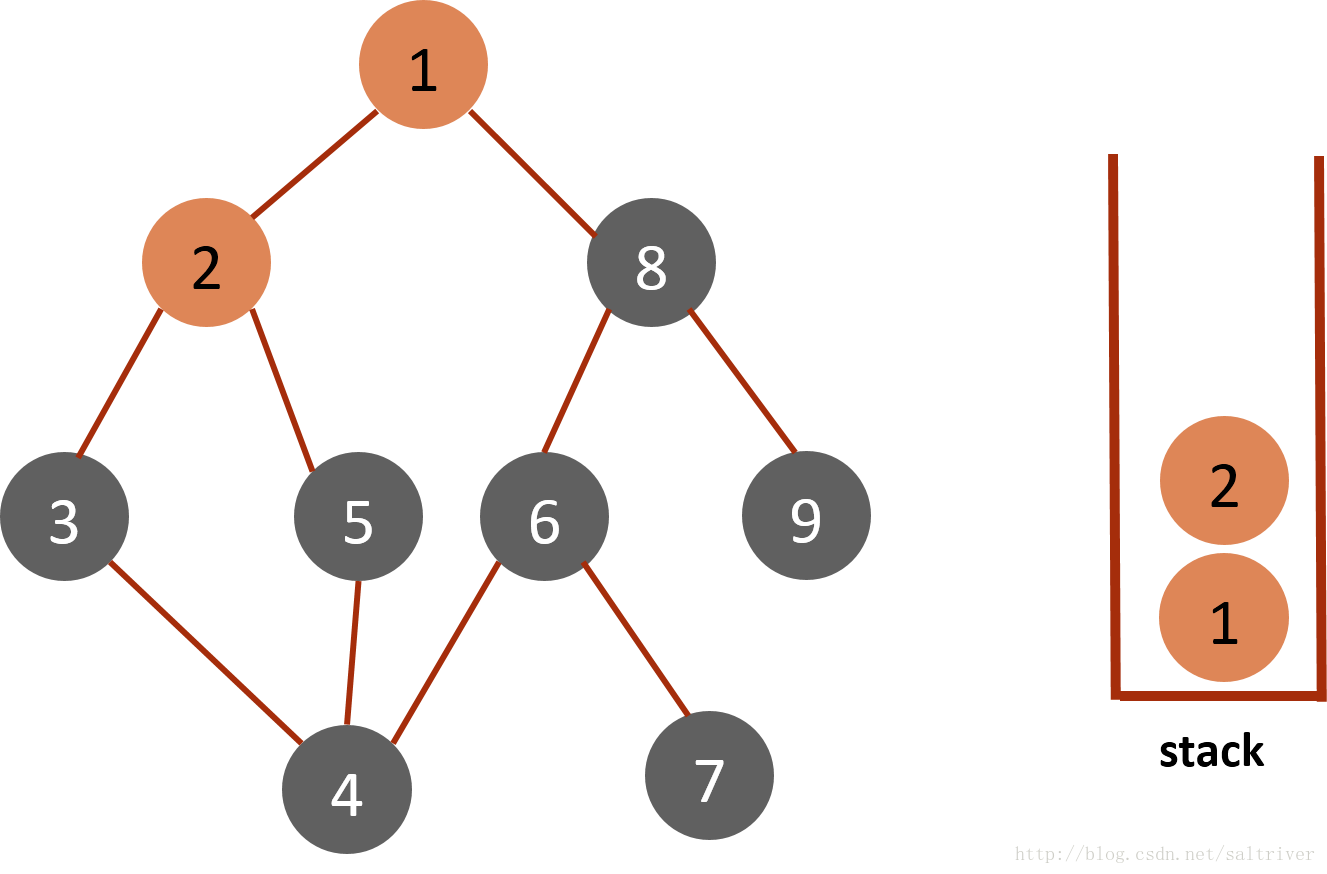
(3)从stack中取出栈顶的节点2,找出与节点2邻接的节点,有1,3,5三个节点,节点1已遍历过,排除;3,5中按照预定的规则选中的是3,标记为已遍历,然后放入stack中。

(4)从stack中取出栈顶的节点3,找出与节点3邻接的节点,有2,4两个节点,节点2已遍历过,排除;选中的是节点4,标记为已遍历,然后放入stack中。
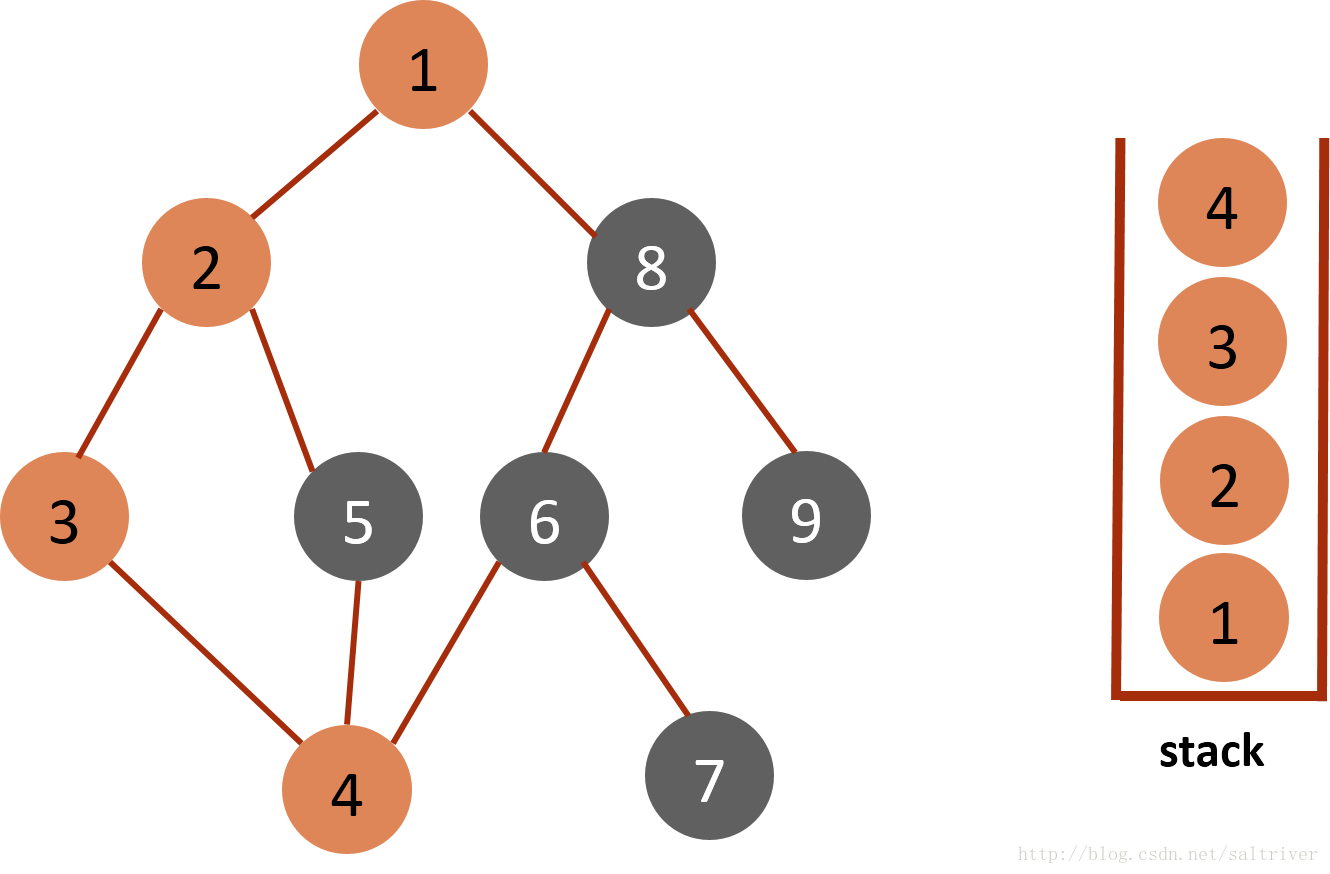
(5)从stack中取出栈顶的节点4,找出与节点4邻接的节点,有3,5,6三个节点,节点3已遍历过,排除;选中的是节点5,标记为已遍历,然后放入stack中。
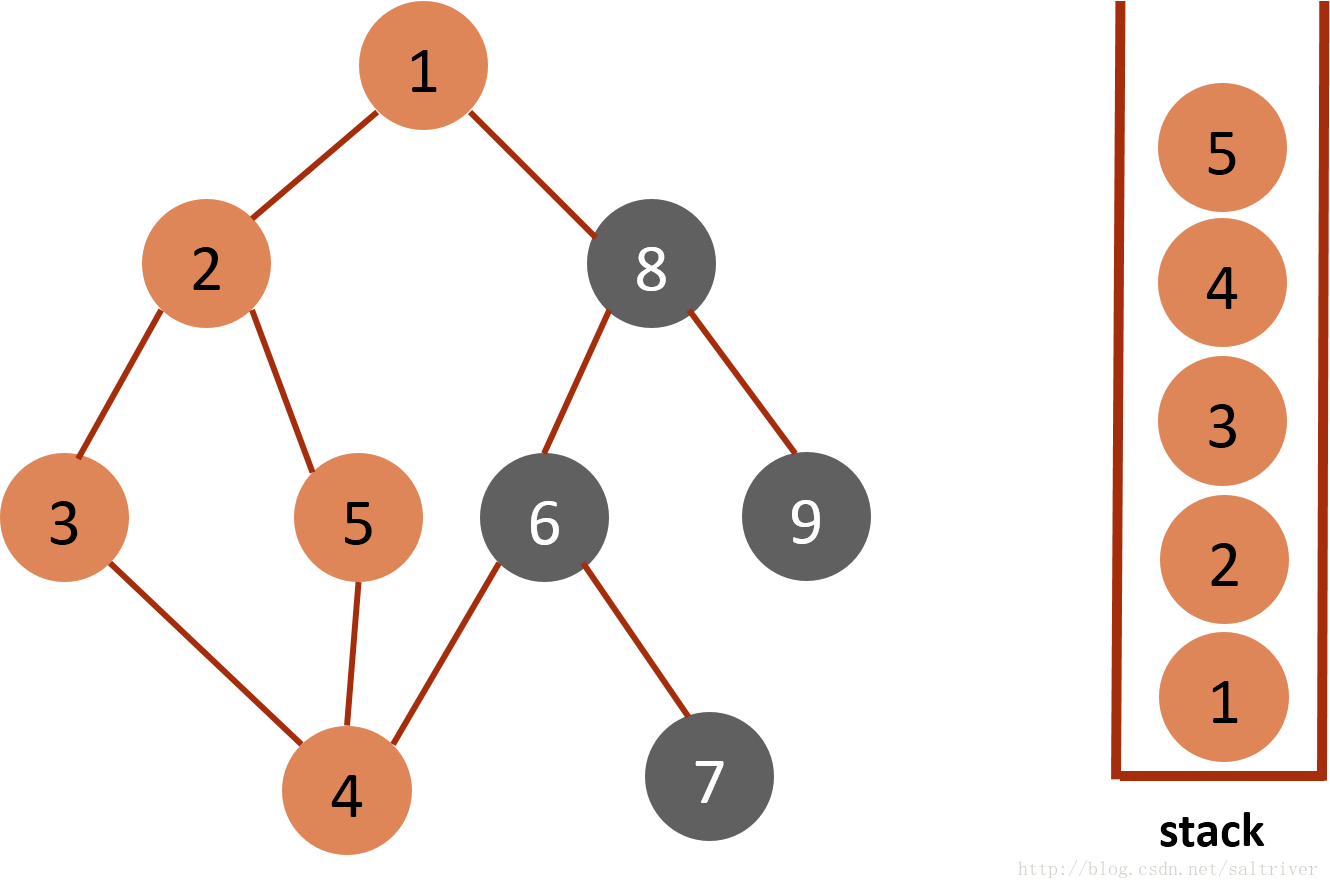
(6)从stack中取出栈顶的节点5,找出与节点5邻接的节点,有2,4两个节点,节点2,4都已遍历过,因此节点5没有尚未遍历的邻接点,则将此点从stack中弹出。

(7)当前stack栈顶的节点是4,找出与节点4邻接的节点,有3,5,6三个节点,节点3,5都已遍历过,排除;选中的是节点6,标记为已遍历,然后放入stack中。
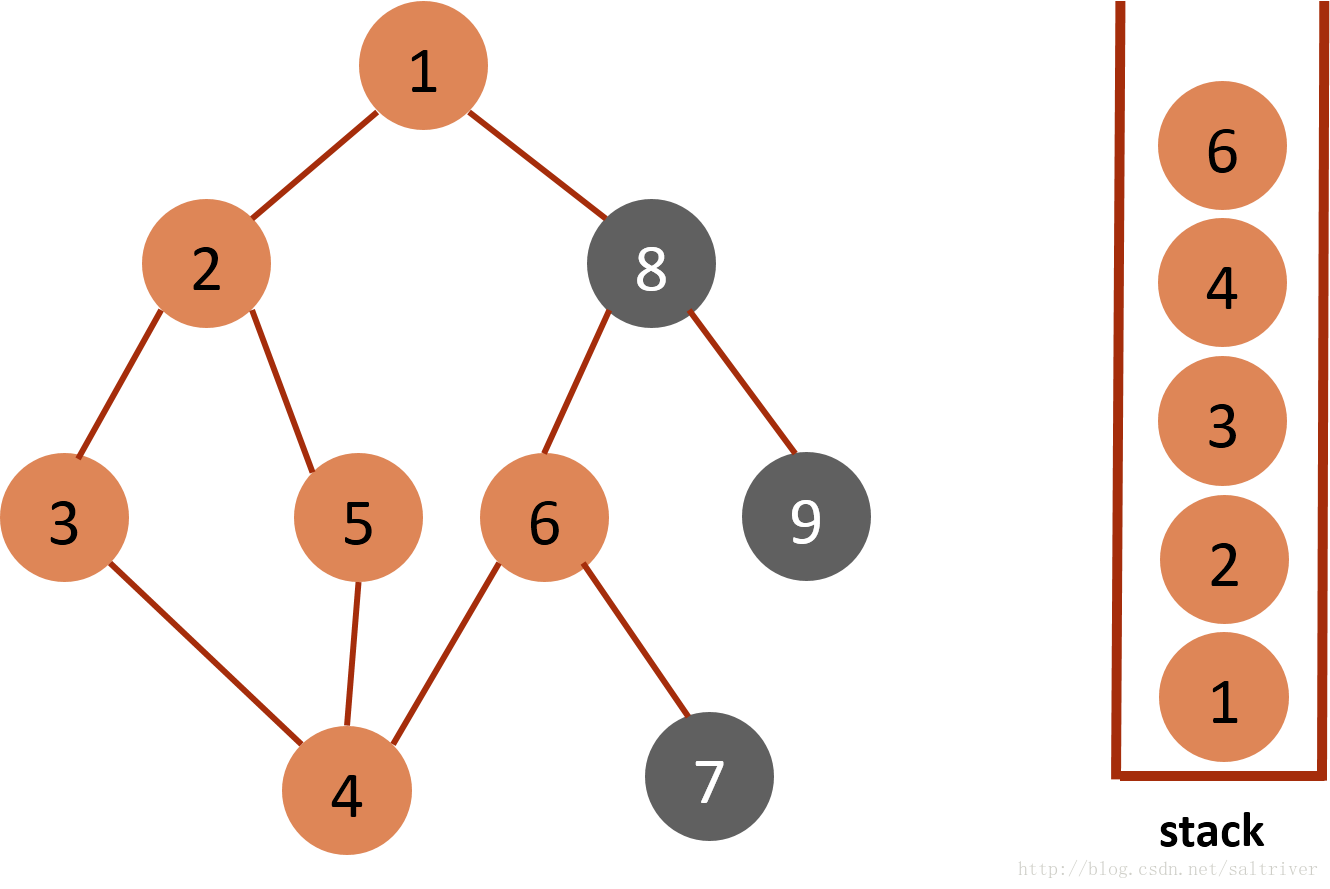
(8)当前stack栈顶的节点是6,找出与节点6邻接的节点,有4,7,8三个节点,4已遍历,按照规则选中的是7,标记为已遍历,然后放入stack中。
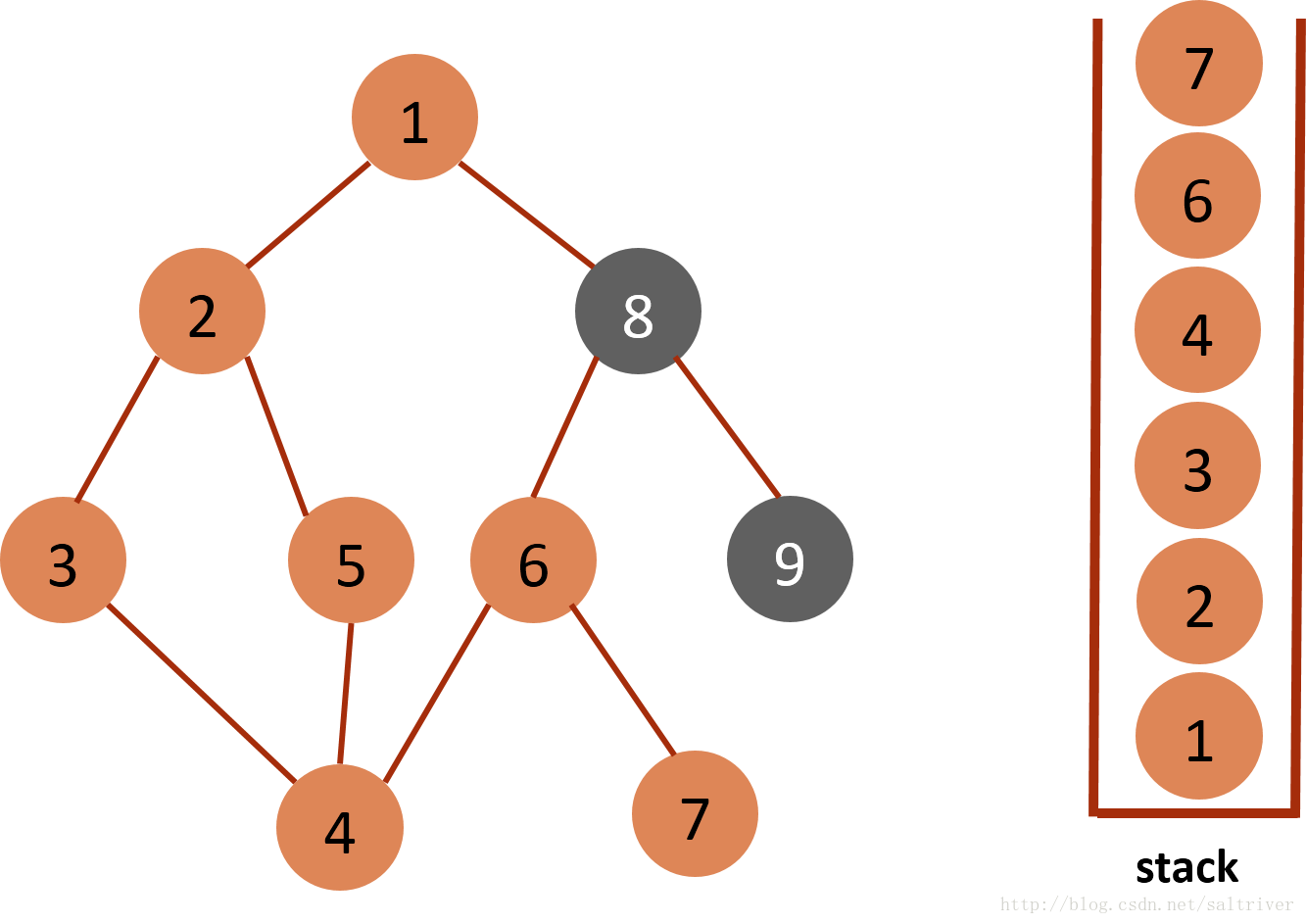
(9)当前stack栈顶的节点是7,找出与节点7邻接的节点,只有节点6,已遍历过,因此没有尚未遍历的邻接点,将节点7从stack中弹出。
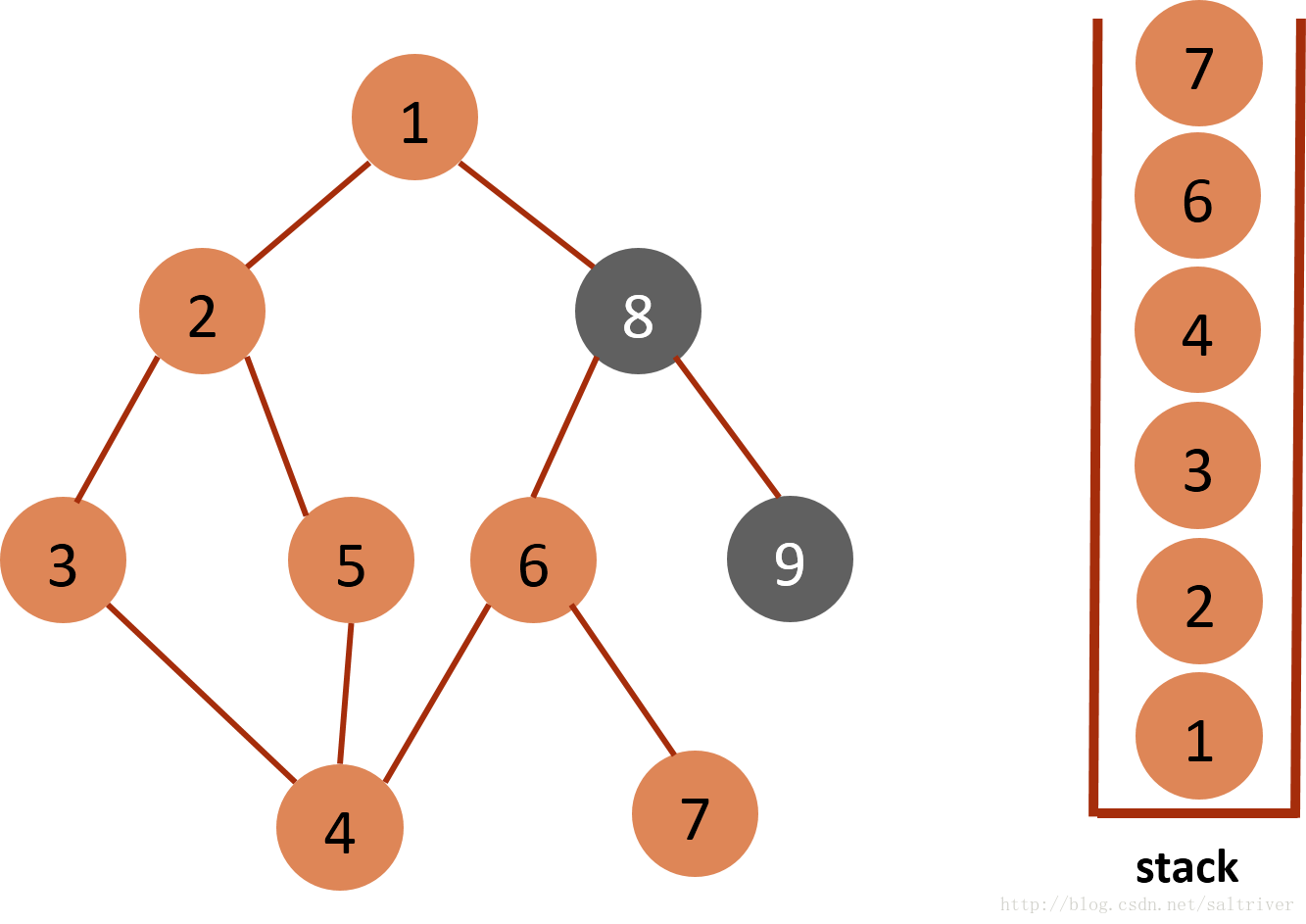
(10)当前stack栈顶的节点是6,找出与节点6邻接的节点,有节点7,8,7已遍历过,因此将节点8放入stack中。
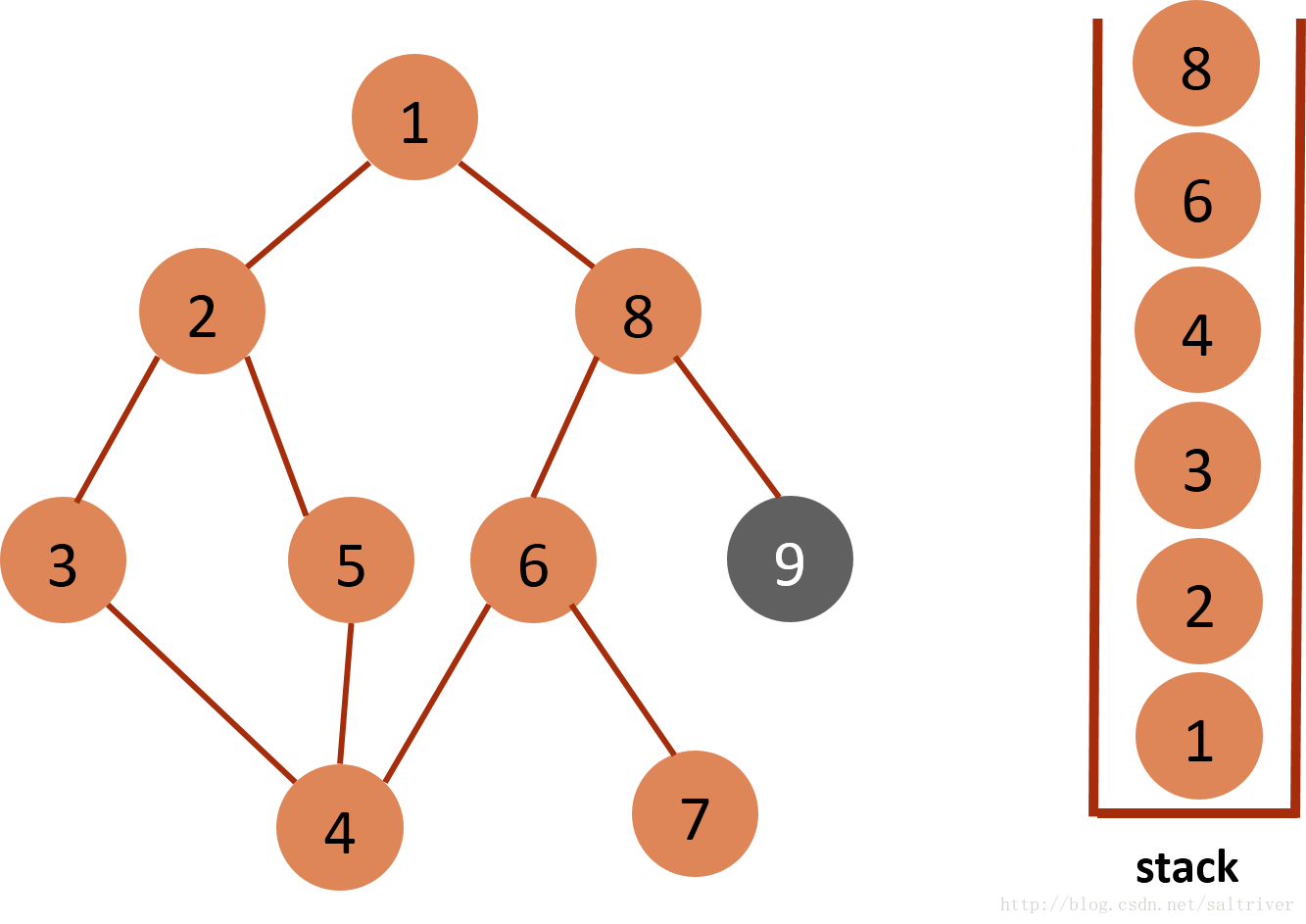
(11)当前stack栈顶的节点是8,找出与节点8邻接的节点,有节点1,6,9,1,6已遍历过,因此将节点9放入stack中。
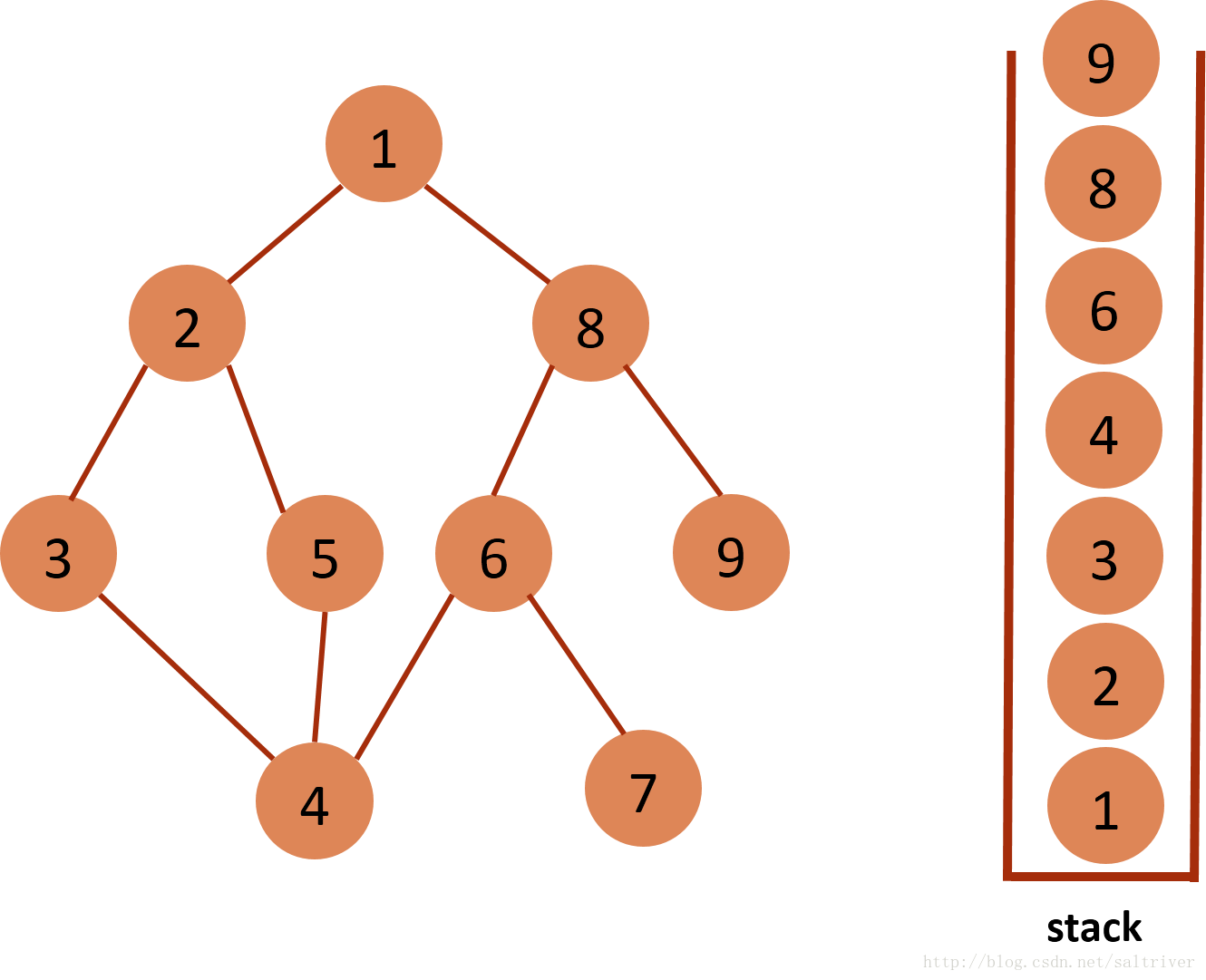
(12)当前stack栈顶的节点是9,没有尚未遍历的邻接点,将节点9弹出,依次类推,栈中剩余节点8,6,4,3,2,1都没有尚未遍历的邻接点,都将弹出,最后栈为空。
(13)DFS遍历完成。
---------------------
作者:saltriver
来源:CSDN
原文:https://blog.csdn.net/saltriver/article/details/54429068
版权声明:本文为博主原创文章,转载请附上博文链接!
应用连接:https://blog.csdn.net/raphealguo/article/details/7560918