在介绍马氏距离之前先看下几个概念:
1 方差:标准差的平方,反映了数据集中数据的离散程度
2 协方差:标准差与方差是衡量一维数据的,当存在多维数据时,要知道每个维度的变量之间是否存在关联,就需使用协方差.协方差是衡量多维数据中,变量之间的相关性.若两个变量之间的协方差为正值,则两个变量间存在正相关,若为负值,则为负相关.
3 协方差矩阵:当变量多了,超过两个了,我们就是用协方差矩阵衡量多变量之间的相关性.
什么是马氏距离呢?
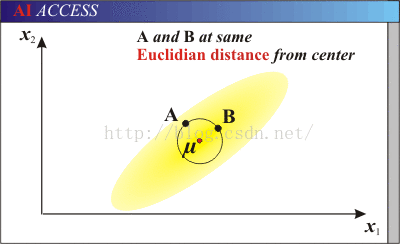
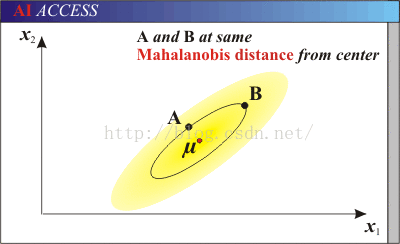
马氏距离与欧式距离不同的是,它考虑到各种特性之间的联系,并且与尺度无关.

当协方差矩阵是单位阵的时候,马氏距离简化为欧氏距离,若协方差矩阵是对角阵时 ,简化为标准化的欧式距离.
马氏距离特性:
1.量纲无关,排除变量之间的相关性的干扰;
2.马氏距离的计算是建立在总体样本的基础上的,如果拿同样的两个样本,放入两个不同的总体中,最后计算得出的两个样本间的马氏距离通常是不相同的,除非这两个总体的协方差矩阵碰巧相同;
3 .计算马氏距离过程中,要求总体样本数大于样本的维数,否则得到的总体样本协方差矩阵逆矩阵不存在,这种情况下,用欧式距离计算即可。
4.还有一种情况,满足了条件总体样本数大于样本的维数,但是协方差矩阵的逆矩阵仍然不存在,比如三个样本点(3,4),(5,6),(7,8),这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下,也采用欧式距离计算。
马氏距离与欧式距离: