搬水果

题目描述：

    在一个果园里，小明已经将所有的水果打了下来，并按水果的不同种类分成了若干堆，小明决定把所有的水果合成一堆。每一次合并，小明可以把两堆水果合并到一起，消耗的体力等于两堆水果的重量之和。当然经过 n‐1 次合并之后，就变成一堆了。小明在合并水果时总共消耗的体力等于每次合并所耗体力之和。

    假定每个水果重量都为 1，并且已知水果的种类数和每种水果的数目，你的任务是设计出合并的次序方案，使小明耗费的体力最少，并输出这个最小的体力耗费值。例如有 3 种水果，数目依次为 1，2，9。可以先将 1，2 堆合并，新堆数目为3，耗费体力为 3。然后将新堆与原先的第三堆合并得到新的堆，耗费体力为 12。所以小明总共耗费体力=3+12=15，可以证明 15 为最小的体力耗费值。

输入：

    每组数据输入包括两行,第一行是一个整数 n(1<=n<=10000),表示水果的种类数，如果 n 等于 0 表示输入结束，且不用处理。第二行包含 n 个整数，用空格分隔，第 i 个整数(1<=ai<=1000)是第 i 种水果的数目。

输出：

对于每组输入，输出一个整数并换行，这个值也就是最小的体力耗费值。输入数据保证这个值小于 2^31。

样例输入：

3
9 1 2
0

样例输出：

15

其实就是各叶节点权值*路径长度之和,当然我们知道霍夫曼树各叶节点权值*路径长度之和最小,用priority_queue实现最小堆,每次选取最小的两个节点,出堆,得其和,和入堆,累加和,循环至堆空,打印累加的和.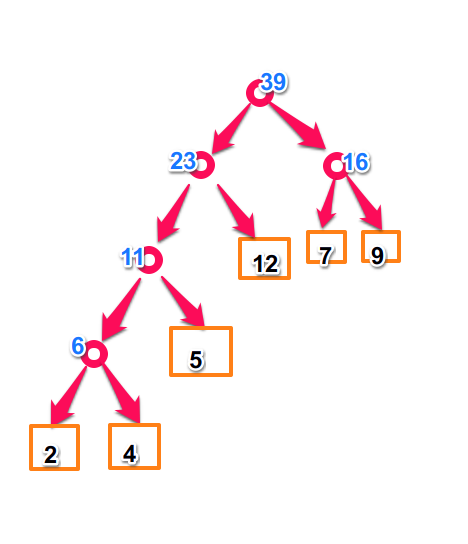

6+11+23+16+39=95

#include "stdio.h"
#include "queue"

using namespace std;

int main()
{
    priority_queue<int , vector <int>,greater<int> > q;//min-heap
    int i,n,t,sum;
//    freopen("in.txt","r",stdin);
    while(scanf("%d",&n)!=EOF&&n!=0)
    {
        for (i=0;i<n;++i)
        {
            scanf("%d",&t);
            q.push(t);
        }
        if(q.size()==1){
            printf("%d\n",q.top());
            q.pop();
            continue;
        }
        sum=0;
        while (!q.empty())
        {
            t=q.top();
            q.pop();
            if (!q.empty())
            {
                t+=q.top();
                sum+=t;
                q.pop();
                q.push(t);
            }
        }
        printf("%d\n",sum);
    }
    return 0;

}