二叉树的题目

1、二叉树的最近公共祖先

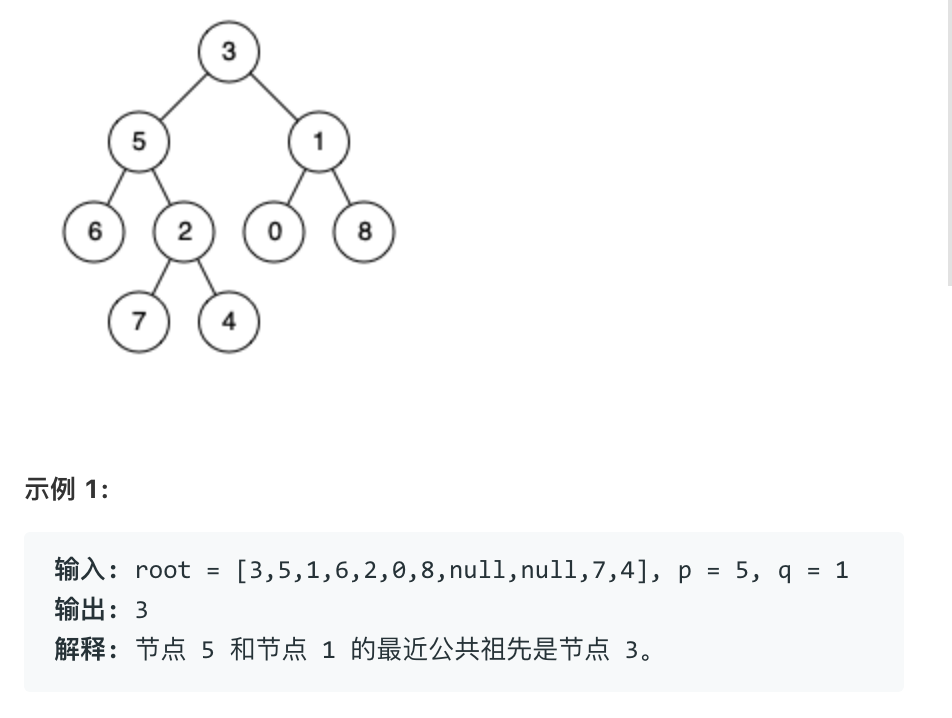
     题目描述：给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

     

　　题解：

      

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        /**
        注意p,q必然存在树内, 且所有节点的值唯一!!!
        递归思想, 对以root为根的(子)树进行查找p和q, 如果root == null || p || q 直接返回root
        表示对于当前树的查找已经完毕, 否则对左右子树进行查找, 根据左右子树的返回值判断:
        1. 左右子树的返回值都不为null, 由于值唯一左右子树的返回值就是p和q, 此时root为LCA
        2. 如果左右子树返回值只有一个不为null, 说明只有p和q存在与左或右子树中, 最先找到的那个节点为LCA
        3. 左右子树返回值均为null, p和q均不在树中, 返回null
        **/
        if(root == null || root == p || root == q) return root;
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if(left == null && right == null) return null;
        else if(left != null && right != null) return root;
        else return left == null ? right : left;
    }
}
例外的题解就是打印从跟节点到 p 和 q的路径，然后求最近公共祖先。

　　2、 二叉搜索树中第K小的元素

           题解： 中序遍历

           

#include <stack>
using std::stack;
class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        //use stack
        stack<TreeNode*> stk;
        int count = 0;
        TreeNode *p = root;
        while(p || !stk.empty())
        {
            if(p)
            {
                stk.push(p);
                p = p->left;
            }
            else
            {
                count++;
                p = stk.top();
                if(count >= k)
                {
                    return p->val;
                }
                p = p->right;
                stk.pop();


            }
            
        }
        return p->val;


    }
};