网络流
在图论中,网络流 (Network Flow) 是指在一个每条边都有容量 (Capacity) 的有向图分配流,使一条边的流量不会超过它的容量。(边有附带容量的图称为网络。)一道流必须符合一个结点的进出的流量相同的限制,除非这是一个源点 (Source) ──有较多向外的流,或是一个汇点 (Sink) ──有较多向内的流。一个网络可以用来模拟道路系统的交通量、管中的液体、电路中的电流或类似一些东西在一个结点 (Node) 的网络中游动的任何事物。
目录[隐藏] |
[编辑]定义
假设 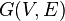 是一个有限的有向图,它的每条边
是一个有限的有向图,它的每条边 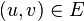 都有一个非负值实数的容量
都有一个非负值实数的容量  。如果
。如果  ,我们假设
,我们假设 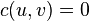 。我们区别两个顶点:一个源点
。我们区别两个顶点:一个源点  和一个汇点
和一个汇点  。一道网络流是一个对于所有结点
。一道网络流是一个对于所有结点  和
和 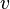 都有以下特性的实数函数
都有以下特性的实数函数  :
:
-
容量限制 (Capacity Constraints):  一条边的流不能超过它的容量。
一条边的流不能超过它的容量。斜对称 (Skew Symmetry): 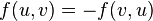 由
由  到
到 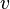 的净流必须是由
的净流必须是由 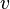 到
到  的净流的相反(参考例子)。
的净流的相反(参考例子)。流守恒 (Flow Conservation): 除非  或
或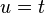 ,否则
,否则 一结点的净流是零,除了“制造”流的源点和“消耗”流的汇点。
一结点的净流是零,除了“制造”流的源点和“消耗”流的汇点。
注意  是由
是由  到
到 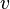 的净流。如果该图代表一个实质的网络,由
的净流。如果该图代表一个实质的网络,由  到
到 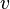 有 4 单位的实际流及由
有 4 单位的实际流及由 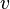 到
到  有 3 单位的实际流,那么
有 3 单位的实际流,那么  及
及  。
。
边的剩余容量 (Residual Capacity) 是 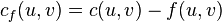 。这定义了以
。这定义了以 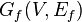 表示的剩余网络 (Residual Network),它显示可用的容量的多少。留意就算在原网络中由
表示的剩余网络 (Residual Network),它显示可用的容量的多少。留意就算在原网络中由  到
到 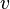 没有边,在剩余网络仍可能有由
没有边,在剩余网络仍可能有由  到
到 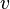 的边。因为相反方向的流抵消,减少由
的边。因为相反方向的流抵消,减少由 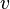 到
到  的流等于增加由
的流等于增加由  到
到 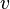 的流。增广路 (Augmenting Path)是一条路径
的流。增广路 (Augmenting Path)是一条路径 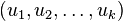 ,而
,而  、
、 及
及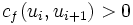 ,这表示沿这条路径传送更多流是可能的。
,这表示沿这条路径传送更多流是可能的。
[编辑]例子
在右边可以看到一个有以  标示的源点、以
标示的源点、以  标示的汇点及 4 个额外结点的流网络。流及容量以
标示的汇点及 4 个额外结点的流网络。流及容量以  显示。注意网络怎样保证斜对称、容量限制及流守恒。由
显示。注意网络怎样保证斜对称、容量限制及流守恒。由  到
到  的总流量为 5,由此可简单地观察到源于
的总流量为 5,由此可简单地观察到源于  的所有向外流是 5,也就是汇于
的所有向外流是 5,也就是汇于  的向内流。我们知道在其它结点中没有任何流出现或消失。
的向内流。我们知道在其它结点中没有任何流出现或消失。
在下面你可以看到对既定的流的剩余网络。注意某些边的剩余容量是正数而原来的容量是零,如边 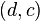 。这道流不是一道最大流。沿路径
。这道流不是一道最大流。沿路径 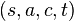 、
、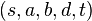 及
及 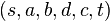 还有可用的容量,也就是扩张路径。第一条路径的剩余容量是
还有可用的容量,也就是扩张路径。第一条路径的剩余容量是  。注意扩张路径
。注意扩张路径 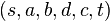 在原来的网络中并不存在,但你可以沿它传送流,因此仍是一道正当的流。
在原来的网络中并不存在,但你可以沿它传送流,因此仍是一道正当的流。
假如这是一个真实的网络,由 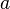 到
到  的 2 单位的流及由
的 2 单位的流及由  到
到 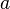 的 1 单位的流事实上可能存在,但我们只维持净流。
的 1 单位的流事实上可能存在,但我们只维持净流。
[编辑]算法
计算最大流最基本的方法是福特富尔克森方法(The Ford-Fulkerson method)、埃德蒙兹卡普算法(The Edmonds-Karp algorithm),由于不同的具体实现方案,其执行效率不同。
此外,也有一些更复杂的方法如“压入与重标记”及“重标记与迁移”等算法,使时间效率进一步提升,最快可达 。
。
[编辑]应用
将一连串的水管绘画成一个网络。每条水管有一特定的阔度,因此只可以保持一特定的水流量。当任何水管汇合,流入汇流点的总水量必须等于流出的水量,否则我们会很快地缺水,或者我们会团积水。我们有一个作为源点的入水口,和一个作为汇点的出水口。一道流便是一条由源点到汇点而使从出水口流出的总水量一致的可能路径。直观地,一个网络的总流量是水从出口流出的速率。
流可以关于在交通网络上的人或物质,或电力分配系统上的电力。对于任何这样的实物网络,进入任何中途结点的流需要等于离开那结点的流。Bollobás以基尔霍夫电流定律描绘这限制的特性,同时较迟的作者(即 Chartrand)提及它在某些守恒方程的普遍化。
在生态学中也可找到流网络的应用:当考虑在食物网中不同组织之间养料及能量的流,流网络便自然地产生。与这些网络有联繋的数学问题和那些液体流或交通流网络中所产生的难题有很大分别。由 Robert Ulanowicz 及其他人发展的生态系统网络分析领域包含使用信息论及热力学的概念去研究这些网络随时间的演变。
[编辑]普遍化及专门化
利用网络流去找出最大流是最简单及最普通的问题,它提供了在一指定的图中由源点到汇点的最大可能总流量。还有很多其它问题可以利用最大流算法去解决,假设它们可以适当地塑造成流网络的模样,例如二部图匹配(Bipartite Matching)、任务分配问题(Assignment Problem)和运输问题(Transportation Problem)。
在多物网络流问题(Multi-commodity Flow Problem)中,可以有多个源点和汇点,和各种各样的由指定源点传送到指定汇点的“物品(Commodities)”。例如这可能是不同的工厂生产的各种各样的货物经由“同一”运输网络运送到不同的消费者手上。
在最少费用流问题(Minimum Cost Flow Problem)中,每条边 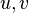 都有特定费用
都有特定费用 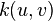 。沿这条边传送
。沿这条边传送  的费用是
的费用是  。目标是要用最低的成本由源点传送一特定数量的流到汇点。
。目标是要用最低的成本由源点传送一特定数量的流到汇点。
在环流问题(Circulation Problem)中,每条边除了有上限  外,还有下限
外,还有下限  。每条边亦有一个费用。很多时,流守恒适用于环流问题中所有结点,由汇点到源点亦有一条连结。这样便能利用
。每条边亦有一个费用。很多时,流守恒适用于环流问题中所有结点,由汇点到源点亦有一条连结。这样便能利用 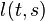 和
和  支配总流量。这问题因流环绕网络流动而得名。
支配总流量。这问题因流环绕网络流动而得名。
在有增益网络或普遍化网络中,每条边都有增益,一个实数(非零)使如果这条边有一增益 g 而有一流量 x 的流在尾部流入,便有一流量 gx 的流从头部流出。

