hdu 2586 How far away?（LCA模板题+离线tarjan算法）

How far away ？

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 25408    Accepted Submission(s): 10111

Problem Description

There are n houses in the village and some bidirectional roads connecting them. Every day peole always like to ask like this "How far is it if I want to go from house A to house B"? Usually it hard to answer. But luckily int this village the answer is always unique, since the roads are built in the way that there is a unique simple path("simple" means you can't visit a place twice) between every two houses. Yout task is to answer all these curious people.

 

Input

First line is a single integer T(T<=10), indicating the number of test cases.
  For each test case,in the first line there are two numbers n(2<=n<=40000) and m (1<=m<=200),the number of houses and the number of queries. The following n-1 lines each consisting three numbers i,j,k, separated bu a single space, meaning that there is a road connecting house i and house j,with length k(0<k<=40000).The houses are labeled from 1 to n.
  Next m lines each has distinct integers i and j, you areato answer the distance between house i and house j.

 

Output

For each test case,output m lines. Each line represents the answer of the query. Output a bland line after each test case.

 

Sample Input

2 3 2 1 2 10 3 1 15 1 2 2 3 2 2 1 2 100 1 2 2 1

 

Sample Output

10 25 100 100

 

 

题目大意：

给你一棵树，求任两点的距离。

 

这是LCA模板题。

求出两点的公共祖先ancst，然后dis[i,j]=depth[i]+depth[j]-depth[ancst]*2；其中depth是节点在有根树中的深度。

离线tarjan算法。。ctrlc ctrlv一段大佬的解释吧。（来自zhouzhendong的cnblogs）

 

LCA_Tarjan

　　TarjanTarjan 算法求 LCA 的时间复杂度为 O(n+q)O(n+q) ，是一种离线算法，要用到并查集。（注：这里的复杂度其实应该不是 O(n+q)O(n+q) ，还需要考虑并查集操作的复杂度 ，但是由于在多数情况下，路径压缩并查集的单次操作复杂度可以看做 O(1)O(1)，所以写成了 O(n+q)O(n+q) 。）

　　TarjanTarjan 算法基于 dfs ，在 dfs 的过程中，对于每个节点位置的询问做出相应的回答。

　　dfs 的过程中，当一棵子树被搜索完成之后，就把他和他的父亲合并成同一集合；在搜索当前子树节点的询问时，如果该询问的另一个节点已经被访问过，那么该编号的询问是被标记了的，于是直接输出当前状态下，另一个节点所在的并查集的祖先；如果另一个节点还没有被访问过，那么就做下标记，继续 dfs 。

　　当然，暂时还没那么容易弄懂，所以建议结合下面的例子和标算来看看。

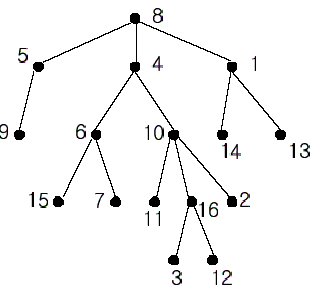
（下面的集合合并都用并查集实现）

　　比如：8−1−14−138−1−14−13 ,此时已经完成了对子树 11 的子树 1414 的 dfsdfs 与合并（ 1414 子树的集合与 11 所代表的集合合并），如果存在询问 (13,14)(13,14) ，则其 LCA 即 getfather(14)getfather(14) ，即 11 ；如果还存在由节点 1313 与 已经完成搜索的子树中的 节点的询问，那么处理完。然后合并子树 1313 的集合与其父亲 11 当前的集合，回溯到子树 11 ，并深搜完所有 11 的其他未被搜索过的儿子，并完成子树 11 中所有节点的合并，再往上回溯，对节点 11 进行类似的操作即可。

 

大意就是，后根dfs一棵树，如果子树遍历完了，就把它整个加入子树根节点的父亲节点的并查集中。

遇到询问，就判断它的另一点是否已经遍历过了，如果是，就getfather。还是自己画画图，应该不难懂吧。

 

第一次写，比较粗糙，附AC代码：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <cmath>
#include <queue>
#include <deque>
#include <stack>
#include <map>
#include <set>
typedef long long LL;
const int MAX_N=40000;
const int MAX_M=200;
const int INF=1000000000;

struct tedge
{
    int to,w,next;
};
tedge edge[MAX_N*2+5];
int head1[MAX_N+5],cnt1;

void addedge(int a,int b,int c)
{
    edge[cnt1]=(tedge){b,c,head1[a]};head1[a]=cnt1++;
    edge[cnt1]=(tedge){a,c,head1[b]};head1[b]=cnt1++;
}

struct tquery
{
    int to,next;
    int index;
};
tquery query[MAX_M*2+5];
int head2[MAX_N+5],cnt2;

void addquery(int a,int b,int i)
{
    query[cnt2]=(tquery){b,head2[a],i};head2[a]=cnt2++;
    query[cnt2]=(tquery){a,head2[b],i};head2[b]=cnt2++;
}

int fa[MAX_N];

int getf(int x)
{
    if(fa[x]==x)
        return x;
    else
        return fa[x]=getf(fa[x]);
}

int vis[MAX_N+5];
int depth[MAX_N+5];
int ans[MAX_M+5];

void LCA(int x,int pa,int dis)
{
    for(int i=head1[x];i!=-1;i=edge[i].next)
    {
        int l=edge[i].to;
        if(l!=pa)
        {
            LCA(l,x,dis+edge[i].w);
        }
    }
    depth[x]=dis;
    for(int i=head2[x];i!=-1;i=query[i].next)
    {
        int l=query[i].to;
        if(vis[l])
        {
            int ancst=getf(l);
            ans[query[i].index]=depth[l]+depth[x]-depth[ancst]*2;
            //printf("%d %d %d
",l,x,ancst);
        }
    }
    fa[x]=pa;vis[x]=1;
}

void init()
{
    memset(head1,-1,sizeof(head1));cnt1=0;
    memset(head2,-1,sizeof(head2));cnt2=0;
    memset(vis,0,sizeof(vis));
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        init();
        int n,m;
        scanf("%d%d",&n,&m);
        for(int i=1,a,b,c;i<=n-1;i++)
        {
            scanf("%d%d%d",&a,&b,&c);
            addedge(a,b,c);
        }
        for(int i=1,a,b;i<=m;i++)
        {
            scanf("%d%d",&a,&b);
            addquery(a,b,i);
        }
        for(int i=1;i<=n;i++)
            fa[i]=i;
        LCA(1,-1,0);
        for(int i=1;i<=m;i++)
            printf("%d
",ans[i]);
    }
    return 0;
}