Problem J. CSGO
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 444 Accepted Submission(s): 220
Problem Description
You are playing CSGO.
There are n Main Weapons and m Secondary Weapons in CSGO. You can only choose one Main Weapon and one Secondary Weapon. For each weapon, it has a composite score S.
The higher the composite score of the weapon is, the better for you.
Also each weapon has K performance evaluations x[1], x[2], …, x[K].(range, firing rate, recoil, weight…)
So you shold consider the cooperation of your weapons, you want two weapons that have big difference in each performance, for example, AWP + CZ75 is a good choose, and so do AK47 + Desert Eagle.
All in all, you will evaluate your weapons by this formula.(MW for Main Weapon and SW for Secondary Weapon)
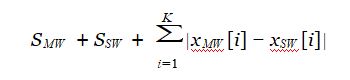
Now you have to choose your best Main Weapon & Secondary Weapon and output the maximum evaluation.
There are n Main Weapons and m Secondary Weapons in CSGO. You can only choose one Main Weapon and one Secondary Weapon. For each weapon, it has a composite score S.
The higher the composite score of the weapon is, the better for you.
Also each weapon has K performance evaluations x[1], x[2], …, x[K].(range, firing rate, recoil, weight…)
So you shold consider the cooperation of your weapons, you want two weapons that have big difference in each performance, for example, AWP + CZ75 is a good choose, and so do AK47 + Desert Eagle.
All in all, you will evaluate your weapons by this formula.(MW for Main Weapon and SW for Secondary Weapon)
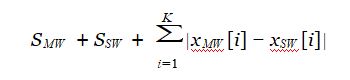
Now you have to choose your best Main Weapon & Secondary Weapon and output the maximum evaluation.
Input
Multiple query.
On the first line, there is a positive integer T, which describe the number of data. Next there are T groups of data.
for each group, the first line have three positive integers n, m, K.
then, the next n line will describe n Main Weapons, K+1 integers each line S, x[1], x[2], …, x[K]
then, the next m line will describe m Secondary Weapons, K+1 integers each line S, x[1], x[2], …, x[K]
There is a blank line before each groups of data.
T<=100, n<=100000, m<=100000, K<=5, 0<=S<=1e9, |x[i]|<=1e9, sum of (n+m)<=300000
On the first line, there is a positive integer T, which describe the number of data. Next there are T groups of data.
for each group, the first line have three positive integers n, m, K.
then, the next n line will describe n Main Weapons, K+1 integers each line S, x[1], x[2], …, x[K]
then, the next m line will describe m Secondary Weapons, K+1 integers each line S, x[1], x[2], …, x[K]
There is a blank line before each groups of data.
T<=100, n<=100000, m<=100000, K<=5, 0<=S<=1e9, |x[i]|<=1e9, sum of (n+m)<=300000
Output
Your output should include T lines, for each line, output the maximum evaluation for the corresponding datum.
Sample Input
2
2 2 1
0 233
0 666
0 123
0 456
2 2 1
100 0 1000 100 1000 100
100 0
Sample Output
543
2000
Source
Recommend
思路:
原题可抽象为在多维曼哈顿路径问题下,求最远点距离。
在坐标轴中,每个数都有+ -两个位置, 一个k维点则会有 2^k种状态。
我们将问题转化为k+2维曼哈顿路径 ,枚举所有点的 2^(k+2)种状态,求最远点距离。
代码如下:

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int inf=1e18; const int maxn=1e5+10; ll a[maxn][7],b[maxn][7],ans,tmp; ll mavm,mivm,mavs,mivs; int _,n,m,k; int main(){ for (scanf("%d",&_); _; _--){ ans=-inf; scanf("%d%d%d",&n,&m,&k); for (int i=1; i<=n; i++){ scanf("%lld",&a[i][0]); for (int j=2; j<=k+1; j++) scanf("%lld",&a[i][j]); } for (int i=1; i<=m; i++){ scanf("%lld",&b[i][1]); for (int j=2; j<=k+1; j++) scanf("%lld",&b[i][j]); } int upp=(1<<k+2); for (int d=0; d<upp; d++){ mavm=-inf,mavs=-inf; mivm=inf,mivs=inf; for (int i=1; i<=n; i++){ tmp=0; for (int j=0; j<k+2; j++){ if(d&(1<<j)) tmp+=a[i][j]; else tmp-=a[i][j]; } mavm=max(mavm,tmp); mivm=min(mivm,tmp); } for (int i=1; i<=m; i++){ tmp=0; for (int j=0; j<k+2; j++){ if(d&(1<<j)) tmp+=b[i][j]; else tmp-=b[i][j]; } mavs=max(mavs,tmp); mivs=min(mivs,tmp); } ans=max(ans,max(mavm-mivs,mavs-mivm)); } printf("%lld ",ans); } return 0; }
