先贴一下树状数组的模板代码:
1 int lowbit(int i) 2 { 3 return i & -i;//或者是return i-(i&(i-1));表示求数组下标二进制的非0最低位所表示的值 4 } 5 void update(int i,int val)//单点更新 6 { 7 while(i<=n){ 8 C[i]+=val; 9 i+=lowbit(i);//由叶子节点向上更新树状数组C,从左往右更新 10 } 11 } 12 int sum(int i)//求区间[1,i]内所有元素的和 13 { 14 int ret=0; 15 while(i>0){ 16 ret+=C[i];//从右往左累加求和 17 i-=lowbit(i); 18 } 19 return ret; 20 }
模板中最常见的三个函数:①取数组下标二进制非0最低位所表示的值;②单点更新;③区间查询。树状数组,顾名思义是树状的数组,我们首先引入二叉树,叶子节点代表A[1]~A[8]。
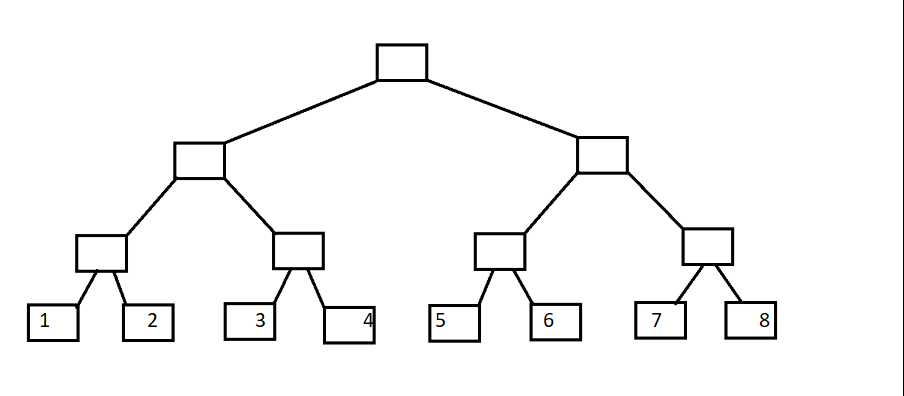
现在变形一下:
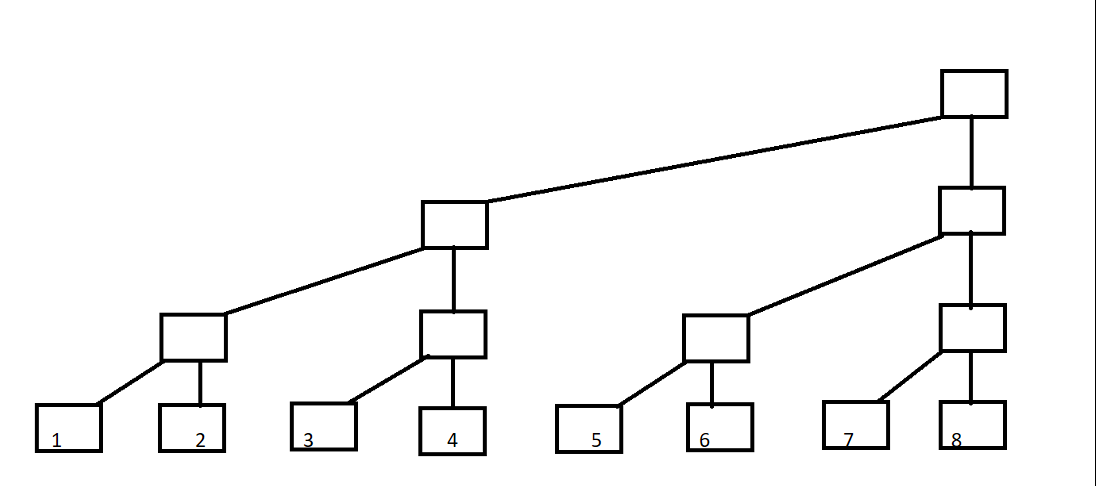
现在定义每一列的顶端节点C数组(其实C数组就是树状数组),如图:
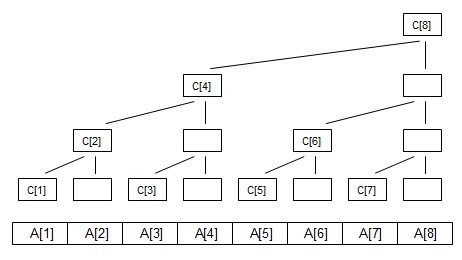
C[i]代表子树的叶子节点的权值之和,如图可以知道:
C[1]=A[1];
C[2]=A[1]+A[2];
C[3]=A[3];
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
C[6]=A[5]+A[6];
C[7]=A[7];
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
将C数组的下标i转化成二进制:
1=(001) C[1]=A[1];
2=(010) C[2]=A[1]+A[2];
3=(011) C[3]=A[3];
4=(100) C[4]=A[1]+A[2]+A[3]+A[4];
5=(101) C[5]=A[5];
6=(110) C[6]=A[5]+A[6];
7=(111) C[7]=A[7];
8=(1000) C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
对照式子可以发现:C[i]=A[i-2^k+1]+A[i-2^k+2]+......+A[i];(k为i的二进制中从最低位到最高位连续零的个数)
例如:当i=8时,k=3,可以自行代入验证。现在引入lowbit(x):其实就是取出x的二进制的最低位1,换言之,lowbit(x)= 2^k,k的含义与上面相同。
1 int lowbit(int i) 2 { 3 return i&(-i); 4 } 5 /* 6 -i 代表i的负数 计算机中负数使用对应的正数的补码来表示 7 例如 : i=6(0110) 此时 k=1 8 -i=-6=(1001+1)=(1010) 9 i&(-i)=(0010)=2=2^1 10 C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; 11 C[i]=A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+......A[i]; 12 */
接下来是区间查询(求和):利用C[i]数组,求A数组中前i项和:举两个栗子:
①i=7,前7项和:sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7];
而C[4]=A[1]+A[2]+A[3]+A[4];C[6]=A[5]+A[6];C[7]=A[7];可以得到:sum[7]=C[4]+C[6]+C[7]。
数组下标写成二进制:sum[(111)]=C[(100)]+C[(110)]+C[(111)];
②i=5,前5项和:sum[5]=A[1]+A[2]+A[3]+A[4]+A[5];
而C[4]=A[1]+A[2]+A[3]+A[4];C[5]=A[5];可以得到:sum[5]=C[4]+C[5];
数组下标写成二进制:sum[(101)]=C[(100)]+C[(101)];
细细观察二进制,树状数组追其根本就是二进制的应用,结合代码演示一下代码过程:
1 int sum(int i)//求区间[1,i]所有元素的和 2 { 3 int ret=0; 4 while(i>0){ 5 ret+=C[i];//从右往左区间求和 6 i-=lowbit(i); 7 } 8 return ret; 9 }
对于i=7进行演示:
7(111) ans+=C[7]
lowbit(7)=001 7-lowbit(7)=6(110) ans+=C[6]
lowbit(6)=010 6-lowbit(6)=4(100) ans+=C[4]
lowbit(4)=100 4-lowbit(4)=0(000) break;
对于i=5进行演示:
5(101) ans+=C[5]
lowbit(5)=001 5-lowbit(5)=4(100) ans+=C[4]
lowbit(4)=100 4-lowbit(4)=0(000) break;
最后是单点更新:当我们修改A数组中某个值时,应当如何更新C数组呢?回想一下,区间查询的过程,再看一下上文中列出的过程。这里声明一下:单点更新实际上是不修改A数组的,而是修改树状数组C,向上更新区间长度为lowbit(i)所代表的节点的值。
1 void update(int i,int val)//更新单节点的值 2 { 3 while(i<=n){ 4 C[i]+=val; 5 i+=lowbit(i);//由叶子节点向上更新a数组 6 } 7 } 8 //可以发现 更新过程是查询过程的逆过程 9 //由叶子结点向上更新C[]数组
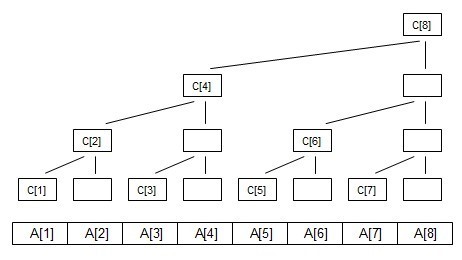
如图:当在A[1]加上值val,即更新A[1]时,需要向上更新C[1],C[2],C[4],C[8],这个时候只需将这4个节点每个节点的值加上val即可。这里为了方便大家理解,人为添加了个A数组表示每个叶子节点的值,事实上A数组并不用修改,实际运用中也可不设置A数组,单点更新只需修改树状数组C即可。下标写成二进制:C[(001)],C[(010)],C[(100)],C[(1000)];
lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=val;
lowbit(2)=010 2+lowbit(2)=4(100) C[4]+=val;
lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=val;
最后说一下树状数组的优缺点:①特点:代码短小,实现简单;容易扩展到高纬度的数据;
②缺点:只能用于求和,不能求最大/小值;不能动态插入;数据多时,空间压力大。