poj 3233 Matrix Power Series（矩阵快速幂）

Description

Given a n × n matrix A and a positive integer k, find the sum S = A + A² + A³ + … + A^k.

Input

The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 10⁹) and m (m < 10⁴). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

Output

Output the elements of S modulo m in the same way as A is given.

Sample Input

2 2 4
0 1
1 1

Sample Output

1 2
2 3
解题思路：等比矩阵求和，采用递归二分的方法。

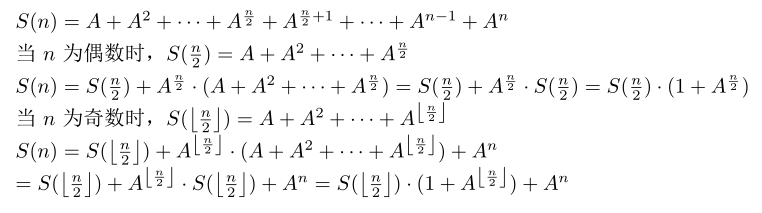
上图就给出了求前k项等比矩阵的和的递推式，解法采用递归来求和比较直观，也很好理解。
AC代码(1704ms)：

#include<iostream>
#include<cstring>
using namespace std;
const int maxn=35;
int n,k,mod;
struct Matrix{int m[maxn][maxn];}init;
Matrix add(Matrix a,Matrix b){//矩阵加法
    Matrix c;
    for(int i=0;i<n;++i)
        for(int j=0;j<n;++j)
            c.m[i][j]=(a.m[i][j]+b.m[i][j])%mod;
    return c;
}
Matrix mul(Matrix a,Matrix b){//矩阵乘法
    Matrix c;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            c.m[i][j]=0;
            for(int k=0;k<n;k++)
                c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
        }
    }
    return c;
}
Matrix quick_power(Matrix a,int x){//矩阵快速幂
    Matrix b;memset(b.m,0,sizeof(b.m));
    for(int i=0;i<n;++i)b.m[i][i]=1;//单位矩阵
    while(x){
        if(x&1)b=mul(b,a);
        a=mul(a,a);x>>=1;
    }
    return b;
}
Matrix sum(Matrix s,int k){//求前k项和
    if(k==1)return s;//递归出口：当幂指数为1时，返回当前的矩阵
    Matrix tmp;memset(tmp.m,0,sizeof(tmp.m));//暂存保存中间的矩阵
    for(int i=0;i<n;++i)tmp.m[i][i]=1;//单位矩阵
    tmp=add(tmp,quick_power(s,k>>1));//计算1+A^{k/2}
    tmp=mul(tmp,sum(s,k>>1));//计算(1+A^{k/2})*(A + A^2 + A^3 + … + A^{k/2})=(1+A^{k/2})*(S_{k/2})
    if(k&1)tmp=add(tmp,quick_power(s,k));//若k是奇数，则加上A^k
    return tmp;//返回前k项的值
}
void print_rectangle(Matrix r){
    for(int i=0;i<n;++i)
        for(int j=0;j<n;++j)
            cout<<r.m[i][j]<<((j==n-1)?"
":" ");
}
int main(){
    while(cin>>n>>k>>mod){
        for(int i=0;i<n;++i)
            for(int j=0;j<n;++j)
                cin>>init.m[i][j];
        init=sum(init,k);
        print_rectangle(init);
    }
    return 0;
}

 采用分块矩阵求解可以减少很多时间，具体推导可以结合下图：

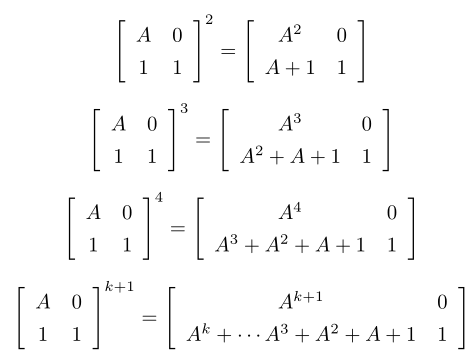
矩阵中套矩阵，效率上比上一种方法更快，实际上是2n×2n的矩阵快速幂。就样例展开等式左边的矩阵：

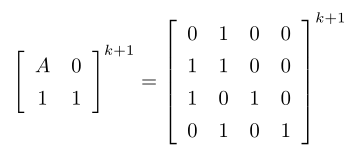
那么最终的答案就是等式右边矩阵中左下角的子矩阵减去单位矩阵，注意某个元素值减-1之后可能为-1，那么此时只需再加上mod即可。

AC代码(610ms)：

#include<iostream>
#include<cstring>
using namespace std;
const int maxn=70;
struct Matrix{int m[maxn][maxn];}init;
int n,k,mod;
Matrix mul(Matrix a,Matrix b){//矩阵乘法
    Matrix c;
    for(int i=0;i<2*n;i++){//矩阵大小扩大两倍，枚举第一个矩阵的行
        for(int j=0;j<2*n;j++){//枚举第二个矩阵的列
            c.m[i][j]=0;
            for(int k=0;k<2*n;k++)//枚举第一个矩阵的列
                c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
        }
    }
    return c;
}
Matrix POW(Matrix a,int x){//矩阵快速幂
    Matrix b;memset(b.m,0,sizeof(b.m));
    for(int i=0;i<2*n;++i)b.m[i][i]=1;//构造单位矩阵
    while(x){
        if(x&1)b=mul(b,a);
        a=mul(a,a);x>>=1;
    }
    return b;
}
void print_rectangle(Matrix r){
    for(int i=0;i<n;++i){
        for(int j=0;j<n;++j){
            if(i==j)r.m[n+i][j]-=1;
            if(r.m[n+i][j]<0)r.m[n+i][j]+=mod;//左下角子矩阵减去单位矩阵，减完可能小于0，因此需要加上mod再取余mod
            cout<<r.m[n+i][j]<<((j==n-1)?'
':' ');
        }
    }
}
int main(){
    while(cin>>n>>k>>mod){
        memset(init.m,0,sizeof(init.m));//全部初始化为0
        for(int i=0;i<n;++i){//首先初始化矩阵
            for(int j=0;j<n;++j)
                cin>>init.m[i][j];
            init.m[n+i][i]=init.m[n+i][n+i]=1;//其余是单位矩阵
        }
        init=POW(init,k+1);//求其前k+1项和（左下角包含单位矩阵，最后输出要减去单位矩阵）
        print_rectangle(init);//打印等比矩阵A前k项和
    }
    return 0;
}