classification

sigmoid function

引入sigmoid函数：(g(z) = frac{1}{1+e^{-z}})
由于(g(z) = frac{e^z}{e^z+1}) 且 (g(-z) = frac{1}{1+e^z})
所以(g(z) + g(-z) = 1) (关于((0,1))对称)
同时(g(z))左边渐近线(y=0)， 右边渐近线(y=1)，(g(0) = 0.5)
自行脑补图像

(g'(z) = frac{-1}{(1+e^{-z})^2} (-e^{-z}) = frac{e^{-z}}{(1+e^{-z})^2} = g(z) * (1 - g(z)) = g(z)g(-z))

逻辑回归logistic regression

binary classification （01label）

新的hypothesis函数改为 (h_{ heta} = g(x heta) = p(y=1|x; heta)) (why?)
其中x是一组example的vector，不是整个X
由上式知(hge 0.5)时估计(y=1)，否则估计(y=0)
所以也就是说(X heta ge 0)时估计(1)
（在一些其他模型里，可以针对问题，调整threshold看F值）

那可能就要问了，那这个g是来干嘛的，搞笑的吗？直接看(x heta)不行么？
一个原因是：代价函数需要用到估计值和真实值，不应该偏差太大（why?）

linear regression的代价函数作用到现在的估价函数上不能保证bowl shape
设计新的代价函数(J( heta) = frac 1 m sum_{i=1}^m cost(h_{ heta}(x^{(i)}),y^{(i)}))
(没有平方的求导需要，不需要2m了)

其中(cost(h_{ heta}(x), y))为一个分段函数
当y=1时，(cost = -log(h_{ heta}(x))) 脑补一下图像
当y=0时，(cost = -log(1-h_{ heta}(x))) 脑补一下图像
也就是说离目标值越近，cost接近0，离目标值远，cost越趋于无穷大
想到可以化简这个分段函数变成跟y有关， 没想出来
可以这样：(cost = -yln(h_{ heta}(x)) -(1-y)ln(1-h_{ heta}(x)))
(1-对1-)

要使用gradient decent, 还得求导
看着就不想求 经过一波大力求导
推出来，竟然跟linear regression的那个形式上完全一样
也是 ( heta_j) -= (frac 1 m sum_{i=1}^m (h_{ heta}(x^{(i)}) - y^{(i)})x^{(i)})

至于一些更快的算法，octave提供了模板
使用方法如下:
先写一个这样的函数

function [J, gradient] = costFunction(theta, X, Y)
    m = length(Y);
    H = sigmoid(X * theta);
    J = -1 / m * (Y' * log(H) + (1.-Y)' * log(1.-H));
    gradient = 1 / m * X' * (H - Y);
end

然后用

options = optimset('GradObj', 'on', 'MaxIter', <iter_limit>);
initialTheta = <some vector of theta>; %起始点
[optimalTheta, optimalJ, exitFlag] = fminunc(@costFunction, initialTheta, options); 
%exitflag: >0迭代次数内收敛，=0表示迭代次数内未收敛，<0表示函数不收敛

多label型（multi-class classification）

one-vs-all
一个一个区分：（类似主元法）
分别计算出(p(y=i|x))
注意这些p不一定和为1
predict时取上述中估计值最大的

朴素贝叶斯naive bayes

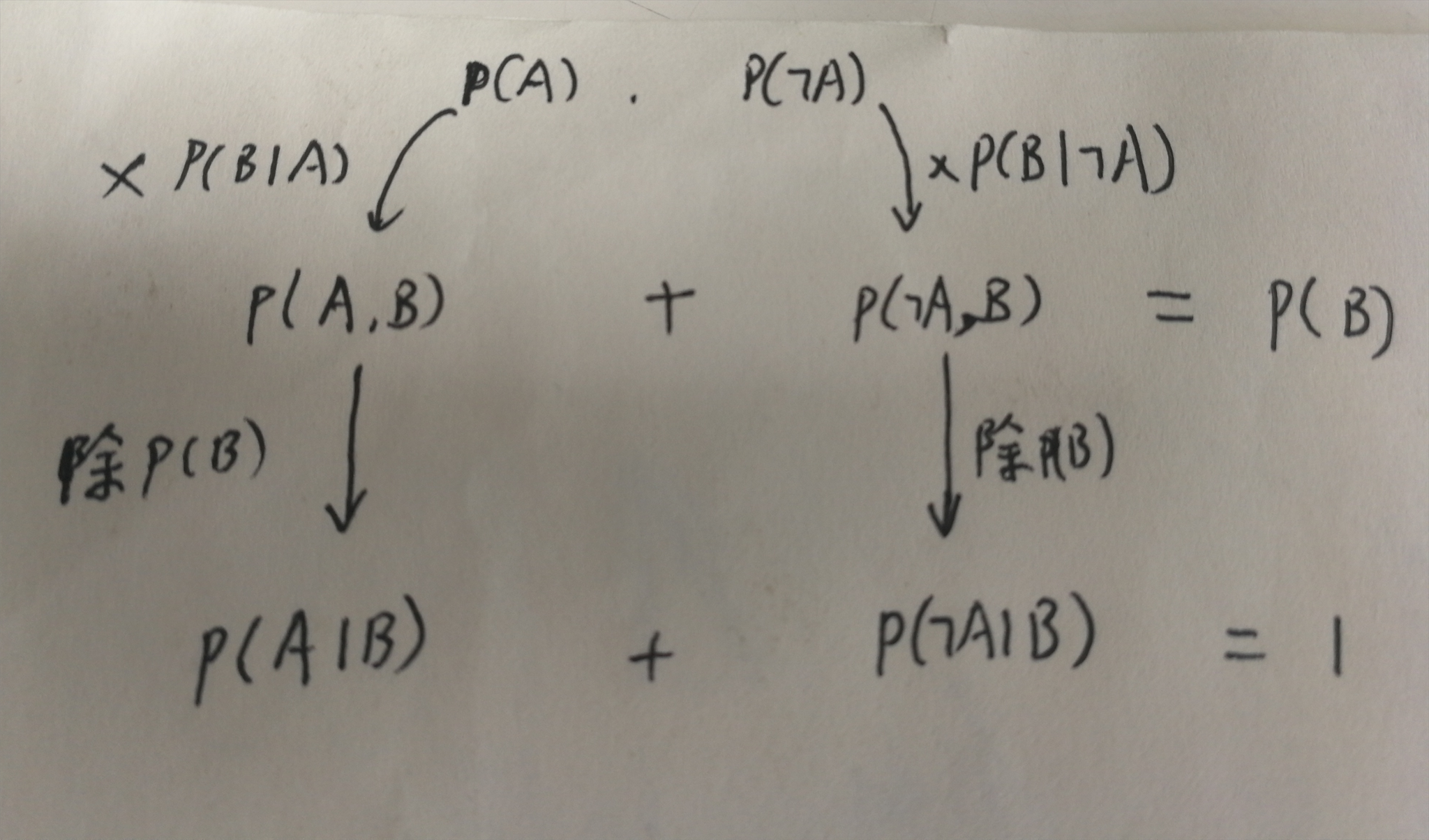
就是概率论那个贝叶斯
获得了一个比较好的贝叶斯的理解

各种类型的NB
高斯型：
二维平面内，给定一些数据点，颜色为红黄蓝绿等等，要找分界线
或一些连续的特征如身高，对应label是性别
预测是根据所处位置，判断处在那个位置的条件下，是哪个作者的概率更大

#features和lables分别用数组对应顺序存起来即可。list,tuple也行，numpy.array也可
from sklearn.naive_bayes import GaussianNB
clf = GaussianNB() #clf = classify
clf.fit(features_train, lables_train) #train
#还有个partial_fit函数,数据量过大不能一次载入内存时,可写几行partial_fit，将数据分成几组
ans = clf.predit(features_test) #predict lables_test（即使只预测一组数据，也要写成数据集合形式）
proba = clf.score(featrues_test, labels_test) #labels_test是已知的预测数据的真实值。  看正确率的 

多项式型：
文章作者辨认问题，根据已有文章训练每个作者用词概率
预测是根据用了那些词及其次数，判这种条件下，是哪个作者的概率更大
缺点是只关注了独立的数据， 而不能整体考虑（词语的顺序，组合等等）
e.g 搜索芝加哥公牛，却搜到大量的公牛和大量的芝加哥城市