bzoj 1367

Description

给定一个序列(t_1,t_2,cdots,t_n)，求一个递增序列(z_1<z_2<...<z_n)，

使得 (R=|t_1−z_1|+|t_2−z_2|+cdots +|t_n−z_n|) 的值最小。求(R)

Analysis

1.转化
(z_1<z_2<...<z_n)的小于号不爽

转化成(z_1le z_2le...le z_n)

我们令(i<j), 根据条件我们有(z_j-z_ige j-i)
移一下项则(z_i-i le z_j-j)
我们令(x_i=t_i-i)，(y_i=z_i-i)
用(x,y)相减是等价的, 且转化成了(y_1le y_2le...le y_n)
后面我们用(x,y)代替(t,z)

2.尝试简单化的题目

假如x单调递增，那么(x_i=y_i)
假如x单调递减呢，(y_1=y_2=cdots=y_n=)x中位数
注：单调递增可以表示为多个单调递减
证明：
假如有条件(y_1=y_2=cdots =y_n), 这个证明不难

现在稍微加一步

①设(y_i)变小，则(y_1...y_{i-1})都变小
若(i<mid)，R显然变大
若(i>mid)，R变大的点数比变小的点数要多

②设(y_i)变大，同理

Solution

对于每个点i一开始属于块i，块中答案(ans_i=x_i)

从前往后扫，维护单调队列, 出现y变小的时候退栈

将两个区间合并,合并后区间的ans变为两块一起的中位数

一直合并, 知道上一个区间的y比当前区间的y小

证明:
首先，合并过的区间一定含有至少一个长度大于1的单调减区间

且一开始，合并过的区间里每个区间都只有一个单调减区间

现在我们要证明的就是两个(多个)单调减区间拼在一起的最优答案也是中位数

跟前面的证明是类似的，如图(绿线辅助线，黑线表示两个单调减区间)

(考虑移动ans那条线)

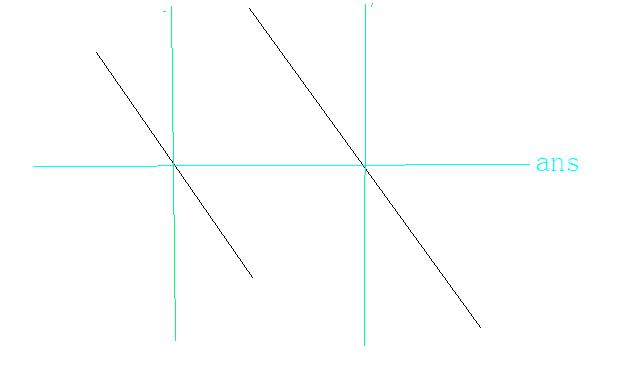
正确性

归纳, 初始答案为(y_1=x_1)

考虑当前加入(x_i)

如果(y_{i-1}le x_i), 显然, 直接令(y_i = x_i)是最优的

当出现(y_{i-1}gt x_i)时, 通过合并操作可以使得答案变优, (y)最大值变小

Code

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <cctype>
#include <algorithm>
using namespace std;
typedef long long LL;
const int M=1000007;
inline int rd(){
	int x=0;bool f=1;char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=1;
	for(;isdigit(c);c=getchar()) x=x*10+c-48;
	return f?x:-x;
}

int n;
int x[M];
struct node{
	int l,r;
	int rt;
	node(int ll=0,int rr=0,int __=0){
		l=ll;r=rr;
		rt=__;
	}
}que[M];
int tt;

int val[M];
int dist[M];
int sz[M];
int lc[M],rc[M];

int merge(int x,int y){
	if(!x) return y;
	if(!y) return x;
	if(val[x]<val[y]) swap(x,y);
	rc[x]=merge(rc[x],y);
	if(dist[rc[x]]>dist[lc[x]]) swap(lc[x],rc[x]);
	dist[x]=dist[rc[x]]+1;
	sz[x]=sz[lc[x]]+sz[rc[x]]+1;
	return x;//*****
}

void pop(int &x){
	x=merge(lc[x],rc[x]);
}

int main(){
	int i,j;
	n=rd();
	for(i=1;i<=n;i++) x[i]=rd()-i;
	for(i=1;i<=n;i++){
		que[++tt]=node(i,i,i);
		val[i]=x[i];
		dist[i]=sz[i]=1;
		while(tt>1&&val[que[tt].rt]<val[que[tt-1].rt]){
			tt--;
			que[tt].r=que[tt+1].r;
			que[tt].rt=merge(que[tt].rt,que[tt+1].rt);
			while(sz[que[tt].rt]*2>(que[tt].r-que[tt].l+2)){
				pop(que[tt].rt);
			}
		}
	}
	LL ans=0;
	for(i=1;i<=n;i++)
	for(j=que[i].l;j<=que[i].r;j++)
		ans+=abs(val[que[i].rt]-x[j]);
	printf("%lld
",ans);
	return 0;
}