题目大意
给出(m)个限制条件
求有多少个满足限制条件的长度为(n)的数(即无前导零)
限制条件形如
(l_1~~r_1~~l_2~~r_2)
表示(s[l_1:r_1]=s[l_r:r_2])
分析
首先每个限制条件,设长度为(len)
我们可以找到一个最大的(k)满足(2^kle len)
用(f[k][i])表示(i)开头的,长度为(2^k)的那一段
那么(s[l_1:r_1]=s[l_r:r_2])
就可以表示为f[k][l_1]=f[k][l_2],f[k][r_1-(1<<k)+1]=f[k][r_2-(1<<k)+1]
做法
既然这样,我们对每个(f[k])就可以用等价关系弄出一个并查集
然后我们从大到小枚举(k)(长度从长到短)
将(2^k)的限制拆成(2^{k-1})的限制
如图
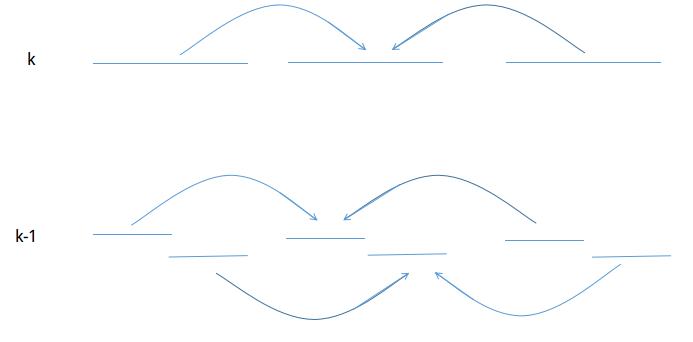
最后就推到最后一层
由于每层最多(n)个起始位置,最多(log)层
所以复杂度是(O(nlog n*并查集))的
由于有“无前导零”的限制
所以一个等价类只能选9个数字
其他都能选10个数字
solution
#include <cstdio>
#include <cstdlib>
#include <cctype>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
const int M=1e5+7;
const int Q=1e9+7;
typedef long long LL;
inline int mul(int x,int y){return 1LL*x*y%Q;}
inline int pls(int x,int y){return ((LL)x+y)%Q;}
inline int mns(int x,int y){return pls(x,Q-y);}
int pwr(int x,int tms){
int res=1;
for(;tms>0;tms>>=1){
if(tms&1) res=mul(res,x);
x=mul(x,x);
}
return res;
}
inline int ri(){
int x=0;bool f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=0;
for(;isdigit(c);c=getchar()) x=x*10+c-48;
return f?x:-x;
}
int n,m;
int ln[M];
int v[M],cnt;
struct dddd{
int dsu[M];
void init(){for(int i=1;i<=n;i++) dsu[i]=i; }
int find(int x){return (dsu[x]!=x)?dsu[x]=find(dsu[x]):x;}
void merge(int x,int y){if(find(x)!=find(y)) dsu[find(x)]=find(y);}
}f[20];
void init(){
int i;
for(i=2;i<=n;i++) ln[i]=ln[i>>1]+1;
}
int main(){
int i,j,x,y,l1,l2,r1,r2;
n=ri(),m=ri();
init();
for(i=0;i<=ln[n];i++) f[i].init();
for(i=1;i<=m;i++){
l1=ri(),r1=ri();
l2=ri(),r2=ri();
j=ln[r1-l1+1];
f[j].merge(l1,l2);
f[j].merge(r1-(1<<j)+1,r2-(1<<j)+1);
}
for(i=ln[n];i>0;i--){
for(j=1;j<=n;j++)
if(f[i].dsu[j]!=j){
l1=j; l2=f[i].dsu[j];
r1=l1+(1<<i)-1; r2=l2+(1<<i)-1;
f[i-1].merge(l1,l2);
f[i-1].merge(r1-(1<<i-1)+1,r2-(1<<i-1)+1);
}
}
for(i=1;i<=n;i++){
x=f[0].find(i);
if(!v[x]) {v[x]=1;cnt++;}
}
printf("%d
",mul(9,pwr(10,cnt-1)));
return 0;
}