AtCoder Regular Contest 099 E

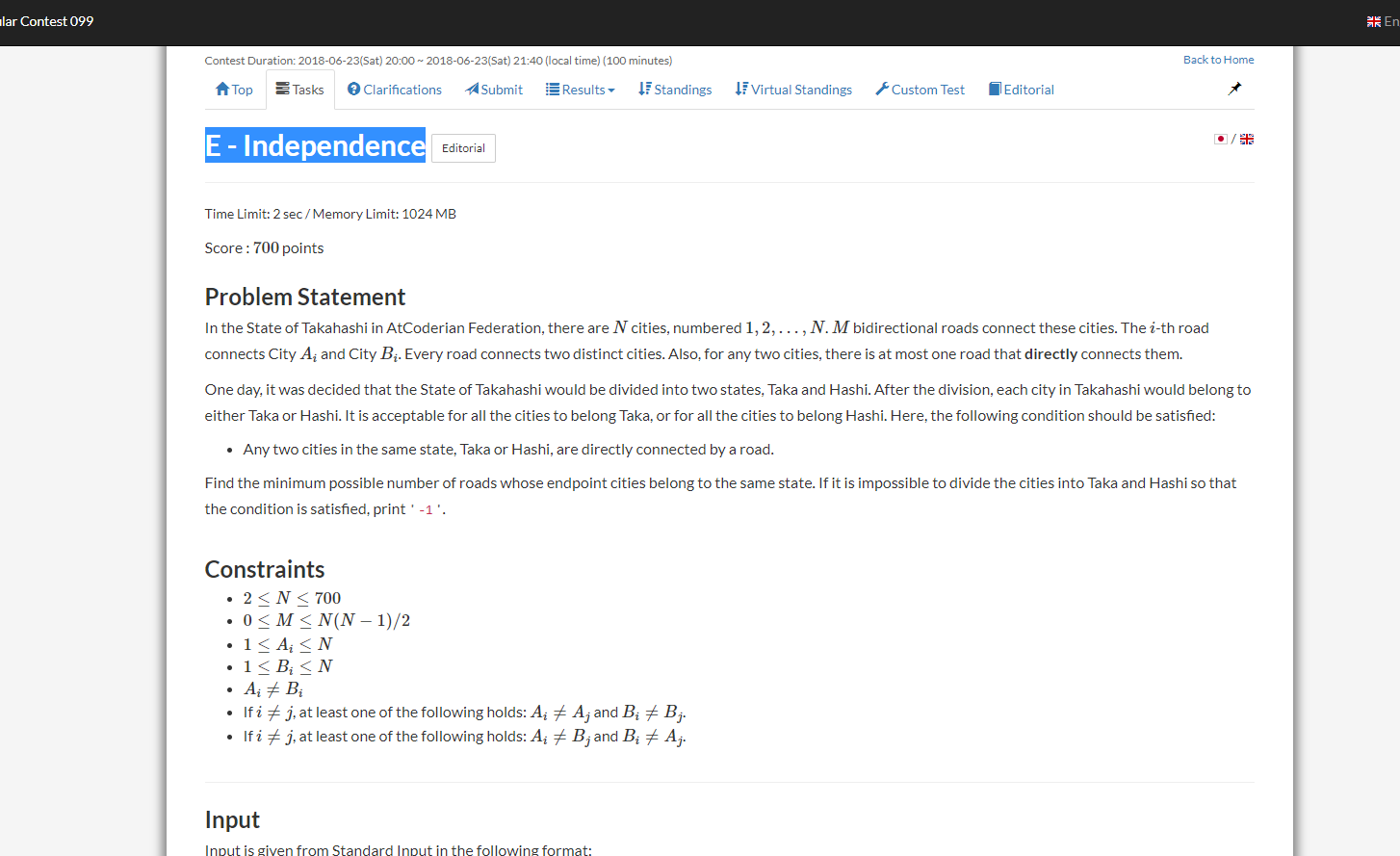
 题意 

给你一个无向图 不会有重边和自环

然后要求你把所有点分成两个集合，每个集合的点必须是个完全图，

如果满足不了上述条件 输出-1；

题解：
考虑建原图的补图；

即，若两点之间没有边，则连边；

若这个图不是二分图，那么无解，感性理解一下就行了

注意你虽然是二分图，但是不一定是全联通，可能是很多个连通二分图组成

然后二分图的各个连通块染色一下，统计左右两边的数目，

最后o（n）的取一下最小值就行了  

然后这个题细节很多，学到了很多细节，建议学习一下代码

#include <bits/stdc++.h>
using namespace std;
const int N=2005;
int n,m;
int g[N][N];
int dp[N],e[N],vis[N],x,y,f=0;
void dfs(int p,int t){
    if (vis[p]){
        if (vis[p]!=t+1)
            f=1;
        return;
    }
    vis[p]=t+1;
    if (t)
        x++;
    else
        y++;
    for (int i=1;i<=n;i++)
        if (i!=p&&!g[p][i])
            dfs(i,t^1);
}
int calc(int x){
    return x*(x-1)/2;
}
int main(){
    scanf("%d%d",&n,&m);
    for (int i=1,a,b;i<=m;i++){
        scanf("%d%d",&a,&b);
        g[a][b]=g[b][a]=1;
    }
    memset(dp,0,sizeof dp);
    dp[0]=1;
    for (int i=1;i<=n;i++){
        if (vis[i])
            continue;
        x=0,y=0;
        dfs(i,0);
        memset(e,0,sizeof e);
        for (int j=n;j>=0;j--)  //注意这个地方的技巧，统计数目答案
            e[j+x]|=dp[j],e[j+y]|=dp[j];
        for (int j=0;j<=n;j++)
            dp[j]=e[j];
    }
    if (f){
        puts("-1");
        return 0;
    }
    int ans=n*n*2;
    for (int i=0;i<=n;i++)
        if (dp[i])//如果出现过，计算一下
            ans=min(ans,calc(i)+calc(n-i));
    printf("%d",ans);
    return 0;
}