[hdu 3949]线性基+高斯消元

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3949

一开始给做出来的线性基wa了很久，最后加了一步高斯消元就过了。

之所以可以这样做，证明如下。

　　首先，把线性基做出来肯定是没有问题的，因为线性基的值域跟原来的n个数的值域是一样的。

　　那么为什么不可以直接用原始的线性基做呢？因为，假设我加入数的顺序是1111,0111,0011,0001（二进制），那么形成的线性基是这样的：

　　这是正常的形成线性基的算法，但是会发现，他们的异或和是杂乱无章的，没很难找到序关系的规律。但是如果我们对这个线性基进行一些高斯消元，变成这样：

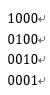
　　序关系就比较显然了，第i大的数，跟i的二进制表示是一一对应的。当然这个比较特殊，事实上高斯消元以后也许会是这样的：

　　事实上我们可以证明这个第i大的数，跟i的二进制表示也是一一对应的。假设i>j，那么用i选出来的一组数的异或和，肯定比j选出来的一组数的异或和大。（因为必然存在某一个二进制位，之前的都相等，这一位i是1，j是0，那么选到的这个数就会导致最后的异或和这一位是1）

//http://acm.hdu.edu.cn/showproblem.php?pid=3949
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

vector<ll> base;
bool insert(ll x)
{
    for (int i=0;i<base.size();i++) x=min(x,x^base[i]);
    if (x) base.push_back(x);
    else return true;
    return false;
}

int main()
{
    int t;
    scanf("%d",&t);
    for (int cas=1;cas<=t;cas++)
    {
        base.clear();
        int n;
        scanf("%d",&n);
        bool flag=false;
        for (int i=1;i<=n;i++)
        {
            ll x;
            scanf("%I64d",&x);
            flag|=insert(x);
        }
        sort(base.begin(),base.end());
        for (int i=base.size()-1;i>=0;i--)
        {
            for (int j=i+1;j<base.size();j++)
            {
                base[j]=min(base[j],base[j]^base[i]);
            }
        }
        int q;
        scanf("%d",&q);
        printf("Case #%d:
",cas);
        while (q--)
        {
            ll k;
            scanf("%I64d",&k);
            if (flag) k--;
            if (k>=(1ll<<base.size())) printf("-1
");
            else
            {
                ll ans=0;
                for (int i=0;i<base.size();i++)
                {
                    if (k&(1ll<<i)) ans^=base[i];
                }
                printf("%I64d
",ans);
            }
        }
    }
    return 0;
}