【数据结构第七周】排序（上）

1、简单排序

void Bubble_Sort( ElemenType A[], int N)
{
	for ( P = N-1; P >= 0 ; P--)
	{
		flag = 0;
		for (i = 0; i < P; ++i)
		{
			if (A[i] > A[i+1])
			{
				Swap(A[i],A[i+1]);
				flag = 1;
			}
		}
		if (flag == 0)
		{
			break;
		}
	}
}

最好情况:顺序T = O( N ) 

最坏情况:逆序 T = O( N^2 ) 

2、插入排序

void Insertion_Sort( ElementType A[], int N)
{
	for ( P = 1; P < N ; ++P)
	{
		Tmp = A[P];
		for (i = P; i > 0 && A[i-1] > Tmp; --i)
		{
			A[i] = A[i-1];
		}
		A[i] = Tmp;

	}
}

最好情况:顺序T = O( N ) 

最坏情况:逆序 T = O( N^2 ) 

定理:任意N个不同元素组成的序列平均具有 N ( N - 1 ) / 4 个逆序对。 

定理:任何仅以交换相邻两元素来排序的算 法,其平均时间复杂度为 Ω ( N^2 ) 。

要提高算法效率,我们必须每次消去不止1个逆序对!每次交换相隔较远的2个元素! 

3、希尔排序

定义增量序列DM >DM-1 >...>D1 =1

原始的希尔排序

DM =N/2, Dk =Dk+1 /2

void Shell_sort( ElementType A[], int N )
{
	for ( D=N/2; D>0; D/=2 )
	{
		for ( P=D; P<N; P++ )
		{
			Tmp = A[P];
			for ( i=P; i>=D && A[i-D]>Tmp; i-=D )
			{
				A[i] = A[i-D];
			}
			A[i] = Tmp;
		}
	}
}

最坏情况：T=θ（N^2）

4、堆排序

堆排序属于选择排序的一种。

选择排序的动画演示，蛮清楚的。http://visualgo.net/sorting.html

void Selection_Sort ( ElementType A[], int N )
{
	for (int i = 0; i < N; ++i)
	{
		MinPosition = ScanForMin( A, i, N–1 );
		/* 从A[i]到A[N–1]中找最小元,并将其位置赋给MinPosition */

		Swap( A[i], A[MinPosition] );
		/* 将未排序部分的最小元换到有序部分的最后位置 */
	}
}

堆排序的平均时间复杂度为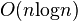，空间复杂度为。

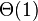堆排序相关资料：http://blog.sina.com.cn/s/blog_54f82cc20100zuho.html

http://zh.wikipedia.org/wiki/%E5%A0%86%E6%8E%92%E5%BA%8F