局部线性嵌入(LLE)原理总结

　局部线性嵌入(Locally Linear Embedding，以下简称LLE)也是非常重要的降维方法。和传统的PCA，LDA等关注样本方差的降维方法相比，LLE关注于降维时保持样本局部的线性特征，由于LLE在降维时保持了样本的局部特征，它广泛的用于图像图像识别，高维数据可视化等领域。下面我们就对LLE的原理做一个总结。

1. 流形学习概述

　　　　LLE属于流形学习(Manifold Learning)的一种。因此我们首先看看什么是流形学习。流形学习是一大类基于流形的框架。数学意义上的流形比较抽象，不过我们可以认为LLE中的流形是一个不闭合的曲面。这个流形曲面有数据分布比较均匀，且比较稠密的特征，有点像流水的味道。基于流行的降维算法就是将流形从高维到低维的降维过程，在降维的过程中我们希望流形在高维的一些特征可以得到保留。

　　　　一个形象的流形降维过程如下图。我们有一块卷起来的布，我们希望将其展开到一个二维平面，我们希望展开后的布能够在局部保持布结构的特征，其实也就是将其展开的过程，就想两个人将其拉开一样。

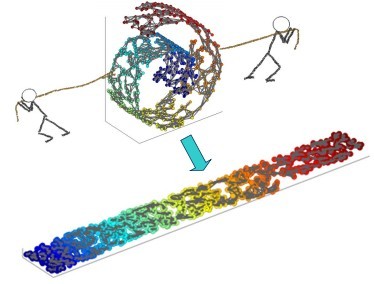
　　　　在局部保持布结构的特征，或者说数据特征的方法有很多种，不同的保持方法对应不同的流形算法。比如等距映射（ISOMAP）算法在降维后希望保持样本之间的测地距离而不是欧式距离，因为测地距离更能反映样本之间在流形中的真实距离。

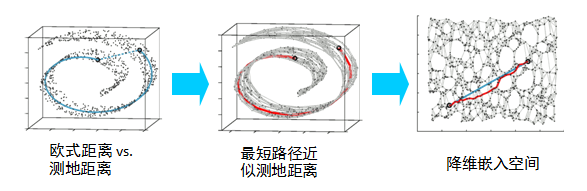
　　　　但是等距映射算法有一个问题就是他要找所有样本全局的最优解，当数据量很大，样本维度很高时，计算非常的耗时，鉴于这个问题，LLE通过放弃所有样本全局最优的降维，只是通过保证局部最优来降维。同时假设样本集在局部是满足线性关系的，进一步减少的降维的计算量。

2. LLE思想

　　　　现在我们来看看LLE的算法思想。

　　　　LLE首先假设数据在较小的局部是线性的，也就是说，某一个数据可以由它邻域中的几个样本来线性表示。比如我们有一个样本x1x1,我们在它的原始高维邻域里用K-近邻思想找到和它最近的三个样本x2,x3,x4x2,x3,x4. 然后我们假设x1x1可以由x2,x3,x4x2,x3,x4线性表示，即：

x1=w12x2+w13x3+w14x4x1=w12x2+w13x3+w14x4

　　　　其中，w12，w13，w14w12，w13，w14为权重系数。在我们通过LLE降维后，我们希望x1x1在低维空间对应的投影x′1x1′和x2,x3,x4x2,x3,x4对应的投影x′2,x′3,x′4x2′,x3′,x4′也尽量保持同样的线性关系，即

x′1≈w12x′2+w13x′3+w14x′4x1′≈w12x2′+w13x3′+w14x4′

　　　　也就是说，投影前后线性关系的权重系数w12，w13，w14w12，w13，w14是尽量不变或者最小改变的。

　　　　从上面可以看出，线性关系只在样本的附近起作用，离样本远的样本对局部的线性关系没有影响，因此降维的复杂度降低了很多。

　　　　下面我们推导LLE算法的过程。

3. LLE算法推导

　　　　对于LLE算法，我们首先要确定邻域大小的选择，即我们需要多少个邻域样本来线性表示某个样本。假设这个值为k。我们可以通过和KNN一样的思想通过距离度量比如欧式距离来选择某样本的k个最近邻。

　　　　在寻找到某个样本的xixi的k个最近邻之后我们就需要找到找到xixi和这k个最近邻之间的线性关系，也就是要找到线性关系的权重系数。找线性关系，这显然是一个回归问题。假设我们有m个n维样本{x1,x2,...,xm}{x1,x2,...,xm},我们可以用均方差作为回归问题的损失函数：即：

J(w)=∑i=1m||xi−∑j=1kwijxj||22J(w)=∑i=1m||xi−∑j=1kwijxj||22

　　　　一般我们也会对权重系数wijwij做归一化的限制，即权重系数需要满足

∑j=1kwij=1∑j=1kwij=1

　　　　对于不在样本xixi邻域内的样本xjxj，我们令对应的wij=0wij=0

　　　　也就是我们需要通过上面两个式子求出我们的权重系数。一般我们可以通过矩阵和拉格朗日子乘法来求解这个最优化问题。

　　　　对于第一个式子，我们先将其矩阵化：

J(W)=∑i=1m||xi−∑j=1kwijxj||22=∑i=1m||∑j=1kwijxi−∑j=1kwijxj||22=∑i=1m||∑j=1kwij(xi−xj)||22=∑i=1m||(xi−xj)Wi||22=∑i=1mWTi(xi−xj)T(xi−xj)Wi(1)(2)(3)(4)(5)(1)J(W)=∑i=1m||xi−∑j=1kwijxj||22(2)=∑i=1m||∑j=1kwijxi−∑j=1kwijxj||22(3)=∑i=1m||∑j=1kwij(xi−xj)||22(4)=∑i=1m||(xi−xj)Wi||22(5)=∑i=1mWiT(xi−xj)T(xi−xj)Wi

　　　　其中Wi=(wi1,wi2,...wik)Wi=(wi1,wi2,...wik)。

　　　　我们令矩阵Zi=(xi−xj)T(xi−xj)Zi=(xi−xj)T(xi−xj),则第一个式子进一步简化为J(W)=∑i=1mWTiZiWiJ(W)=∑i=1mWiTZiWi.对于第二个式子，我们可以矩阵化为：

∑j=1kwij=WTi1k=1∑j=1kwij=WiT1k=1

　　　　其中1k1k为k维全1向量。

　　　　现在我们将矩阵化的两个式子用拉格朗日子乘法合为一个优化目标：

L(W)=∑i=1mWTiZiWi+λ(WTi1k−1)L(W)=∑i=1mWiTZiWi+λ(WiT1k−1)

　　　　对WW求导并令其值为0，我们得到

2ZiWi+λ1k=02ZiWi+λ1k=0

　　　　即我们的

Wi=λ′Z−1i1kWi=λ′Zi−11k

　　　　其中 λ′=−12λλ′=−12λ为一个常数。利用 WTi1k=1WiT1k=1,对WiWi归一化，那么最终我们的权重系数WiWi为：

Wi=Z−1i1k1TkZ−1i1kWi=Zi−11k1kTZi−11k

　　　　现在我们得到了高维的权重系数，那么我们希望这些权重系数对应的线性关系在降维后的低维一样得到保持。假设我们的n维样本集{x1,x2,...,xm}{x1,x2,...,xm}在低维的d维度对应投影为{y1,y2,...,ym}{y1,y2,...,ym}, 则我们希望保持线性关系，也就是希望对应的均方差损失函数最小，即最小化损失函数J(Y)J(Y)如下：

J(y)=∑i=1m||yi−∑j=1kwijyj||22J(y)=∑i=1m||yi−∑j=1kwijyj||22

　　　　可以看到这个式子和我们在高维的损失函数几乎相同，唯一的区别是高维的式子中，高维数据已知，目标是求最小值对应的权重系数WW,而我们在低维是权重系数WW已知，求对应的低维数据。

　　　　为了得到标准化的低维数据，一般我们也会加入约束条件如下：

∑i=1myi=0;1m∑i=1myiyTi=I∑i=1myi=0;1m∑i=1myiyiT=I

　　　　首先我们将目标损失函数矩阵化：

J(Y)=∑i=1m||yi−∑j=1kwijyj||22=∑i=1m||YIi−YWi||22=tr(YT(I−W)T(I−W)Y)(6)(7)(8)(6)J(Y)=∑i=1m||yi−∑j=1kwijyj||22(7)=∑i=1m||YIi−YWi||22(8)=tr(YT(I−W)T(I−W)Y)

　　　　如果我们令M=(I−W)T(I−W)M=(I−W)T(I−W),则优化函数转变为最小化下式：J(Y)=tr(YTMY)J(Y)=tr(YTMY),tr为迹函数。约束函数矩阵化为：YTY=mIYTY=mI

　　　　如果大家熟悉谱聚类和PCA的优化，就会发现这里的优化过程几乎一样。其实最小化J(Y)对应的Y就是M的最小的d个特征值所对应的d个特征向量组成的矩阵。当然我们也可以通过拉格朗日函数来得到这个:

L(Y)=tr(YTMY)+λ(YTY−mI)L(Y)=tr(YTMY)+λ(YTY−mI)

　　　　对Y求导并令其为0，我们得到2MY+2λY=02MY+2λY=0,即MY=λYMY=λY,这样我们就很清楚了，要得到最小的d维数据集，我们需要求出矩阵M最小的d个特征值所对应的d个特征向量组成的矩阵Y=(y1,y2,...yd)Y=(y1,y2,...yd)即可。

　　　　一般的，由于M的最小特征值为0不能反应数据特征，此时对应的特征向量为全1。我们通常选择M的第2个到第d+1个最小的特征值对应的特征向量M=(y2,y3,...yd+1)M=(y2,y3,...yd+1)来得到最终的Y。为什么M的最小特征值为0呢？这是因为WTe=eWTe=e, 得到|WT−I|e=0|WT−I|e=0,由于e≠0e≠0,所以只有WT−I=0WT−I=0,即 (I−W)T=0(I−W)T=0,两边同时右乘I−WI−W，即可得到(I−W)T(I−W)e=0e(I−W)T(I−W)e=0e,即M的最小特征值为0.

4. LLE算法流程

　　　　在上一节我们已经基本推导了LLE降维的整个流程，现在我们对算法过程做一个总结。整个LLE算法用一张图可以表示如下：

　　　　从图中可以看出，LLE算法主要分为三步，第一步是求K近邻的过程，这个过程使用了和KNN算法一样的求最近邻的方法。第二步，就是对每个样本求它在邻域里的K个近邻的线性关系，得到线性关系权重系数W，具体过程在第三节第一部分。第三步就是利用权重系数来在低维里重构样本数据，具体过程在第三节第二部分。

　　　　具体过程如下：

　　　　输入：样本集D={x1,x2,...,xm}D={x1,x2,...,xm}, 最近邻数k，降维到的维数d

　　　　输出： 低维样本集矩阵D′D′

　　　　1) for i 1 to m,  按欧式距离作为度量，计算和xixi最近的的k个最近邻(xi1,xi2,...,xik,)(xi1,xi2,...,xik,)

　　　　2) for i 1 to m, 求出局部协方差矩阵Zi=(xi−xj)T(xi−xj)Zi=(xi−xj)T(xi−xj),并求出对应的权重系数向量:

Wi=Z−1i1k1TkZ−1i1kWi=Zi−11k1kTZi−11k

　　　　3) 由权重系数向量WiWi组成权重系数矩阵WW,计算矩阵M=(I−W)T(I−W)M=(I−W)T(I−W)

　　　　4) 计算矩阵M的前d+1个特征值，并计算这d+1个特征值对应的特征向量{y1,y2,...yd+1}{y1,y2,...yd+1}。

　　　　5）由第二个特征向量到第d+1个特征向量所张成的矩阵即为输出低维样本集矩阵D′=(y2,y3,...yd+1)D′=(y2,y3,...yd+1)　　　　　　

5. LLE的一些改进算法

　　　　LLE算法很简单高效，但是却有一些问题，比如如果近邻数k大于低维的维度d时，我们的权重系数矩阵不是满秩的。为了解决这样类似的问题，有一些LLE的变种产生出来。比如：Modified Locally Linear Embedding(MLLE)和Hessian Based LLE(HLLE)。对于HLLE，它不是考虑保持局部的线性关系，而是保持局部的Hessian矩阵的二次型的关系。而对于MLLE，它对搜索到的最近邻的权重进行了度量，我们一般都是找距离最近的k个最近邻就可以了，而MLLE在找距离最近的k个最近邻的同时要考虑近邻的分布权重，它希望找到的近邻的分布权重尽量在样本的各个方向，而不是集中在一侧。

　　　　另一个比较好的LLE的变种是Local tangent space alignment(LTSA)，它希望保持数据集局部的几何关系，在降维后希望局部的几何关系得以保持，同时利用了局部几何到整体性质过渡的技巧。

　　　　这些算法原理都是基于LLE，基本都是在LLE这三步过程中寻求优化的方法。具体这里就不多讲了。

6. LLE总结

　　　　LLE是广泛使用的图形图像降维方法，它实现简单，但是对数据的流形分布特征有严格的要求。比如不能是闭合流形，不能是稀疏的数据集，不能是分布不均匀的数据集等等，这限制了它的应用。下面总结下LLE算法的优缺点。

　　　　LLE算法的主要优点有：

　　　　1）可以学习任意维的局部线性的低维流形

　　　　2）算法归结为稀疏矩阵特征分解，计算复杂度相对较小，实现容易。

　　　　LLE算法的主要缺点有：

　　　　1）算法所学习的流形只能是不闭合的，且样本集是稠密均匀的。

　　　　2）算法对最近邻样本数的选择敏感，不同的最近邻数对最后的降维结果有很大影响。