1212 无向图最小生成树
N个点M条边的无向连通图,每条边有一个权值,求该图的最小生成树。
收起
输入
第1行:2个数N,M中间用空格分隔,N为点的数量,M为边的数量。(2 <= N <= 1000, 1 <= M <= 50000)
第2 - M + 1行:每行3个数S E W,分别表示M条边的2个顶点及权值。(1 <= S, E <= N,1 <= W <= 10000)输出
输出最小生成树的所有边的权值之和。输入样例
9 14
1 2 4
2 3 8
3 4 7
4 5 9
5 6 10
6 7 2
7 8 1
8 9 7
2 8 11
3 9 2
7 9 6
3 6 4
4 6 14
1 8 8输出样例
37Prim算法是直接查找,多次寻找邻边的权重最小值,而Kruskal是需要先对权重排序后查找的,所以,Kruskal在算法效率上是比Prim快的,因为Kruskal只需一次对权重的排序就能找到最小生成树,而Prim算法需要多次对邻边排序才能找到。
(1)kruskal做法(时间复杂度:O(n*n)):
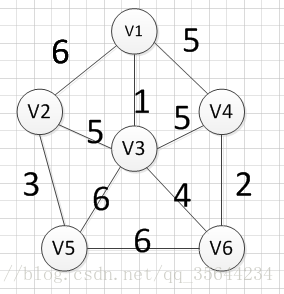
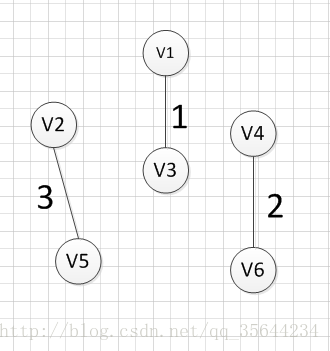
定义每个结点的初始祖先为自己,按照边的大小将结构体排序,然后依次遍历结构体,并查集查找祖先:
1、如果两结点的祖宗节点不一样,则将其中一个结点的祖宗作为(另一个节点的祖宗)的祖宗,对应的边即为最小生成树的边
2、如果两结点祖宗一样,则前面已将两结点连在一棵树上,对应的边不是最小生成树的边
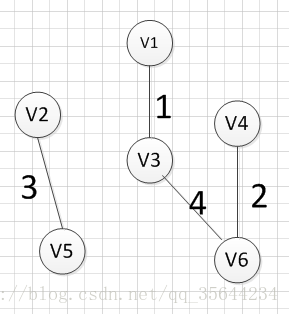
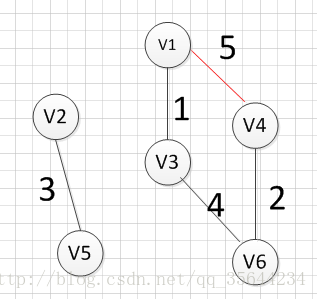
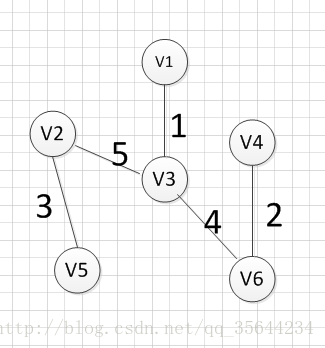
图三遍历到v3,v4连接的边,发现祖宗不同,所以将此边加入树中,图四遍历到v1,v4连接边,但是他们的祖宗(v1,v3,v4,v6中的一点)相同,所以不能加入,图五遍历到v3,v5连接的边,发现祖宗不同,所以将此边加入树中
#include<string.h>
#include<algorithm>
#define inf 9999999
using namespace std;
struct pt{
int s,e,dis;
}a[50011];
int f[1011];
int find(int x){//并查集,寻找祖先
return x==f[x]?f[x]:find(f[x]);
}
bool cmp(pt x,pt y){
return x.dis<y.dis;
}
bool judge(pt p){
int s=find(p.s);//p.s的祖先
int e=find(p.e);//p.e的祖先
if(s!=e){//祖先不一样说明不同一棵树上
f[s]=e;//将两个中的一个定义为共同祖先
return 1;
}
else
return 0;
}
int main()
{
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
f[i]=i;
for(int i=0;i<m;i++)
scanf("%d %d %d",&a[i].s,&a[i].e,&a[i].dis);
sort(a,a+m,cmp);
int ans=0,cnt=0;
for(int i=0;i<m;i++){
if(judge(a[i])){
ans+=a[i].dis;
cnt++;
if(cnt==n-1)//边数达到m-1说明全部点都在树上了
break;
}
}
printf("%d
",ans);
return 0;
}
(2)prime做法(时间复杂度:O(n^2)):
对点进行操作,从起始点开始遍历找与当前点连接最近的点,每找出一个点更新一遍剩余点的拓展边(替换为最小值),各点最短拓展边的和即为结果;

#include<iostream>
#include<algorithm>
#include<string.h>
#define inf 9999999
using namespace std;
bool vis[1011];
int d[1011][1011],dis[1011];
int main()
{
int n,m,x,y,z;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++)
d[i][j]=d[j][i]=inf;
}
for(int i=0;i<m;i++){
scanf("%d%d%d",&x,&y,&z);
d[x][y]=d[y][x]=z;
}
for(int i=1;i<=n;i++)
dis[i]=d[1][i];//初始化到i点连接边为1到i的距离
vis[1]=1;
int mi,id,ans=0;
for(int k=1;k<n;k++)//遍历剩下的n个点
{
mi=inf;id=-1;
for(int i=1;i<=n;i++)
if(!vis[i]&&mi>dis[i])
mi=dis[i],id=i;//找出拓展边最短的点
vis[id]=1;
ans+=mi;
for(int i=1;i<=n;i++)//更新未访问点的最短拓展边
if(!vis[i]&&dis[i]>d[id][i])
dis[i]=d[id][i];
}
printf("%d
",ans);
return 0;
}