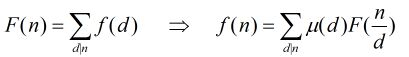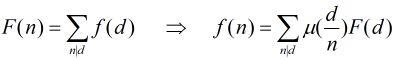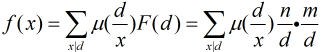HDU 1695 GCD （莫比乌斯反演模板）

GCD

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 17212    Accepted Submission(s): 6637

Problem Description
Given 5 integers: a, b, c, d, k, you're to find x in a...b, y in c...d that GCD(x, y) = k. GCD(x, y) means the greatest common divisor of x and y. Since the number of choices may be very large, you're only required to output the total number of different number pairs.
Please notice that, (x=5, y=7) and (x=7, y=5) are considered to be the same.

Yoiu can assume that a = c = 1 in all test cases.

Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 3,000 cases.
Each case contains five integers: a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000, as described above.

Output
For each test case, print the number of choices. Use the format in the example.

Sample Input
2
1 3 1 5 1
1 11014 1 14409 9
 

Sample Output
Case 1: 9
Case 2: 736427

Hint

For the first sample input, all the 9 pairs of numbers are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 5), (3, 4), (3, 5). 

题解：

题意是求满足1<=x<=b和1<=y<=d的gcd(x,y)=k的(x,y)有多少对，可以转化为求1<=x<=b/k和1<=y<=d/k的gcd(x,y)=1的(x,y)有多少对，可以用到莫比乌斯反演解决,证明链接https://blog.csdn.net/outer_form/article/details/50588307

       

       

这里运用到第二个式子：

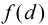
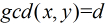
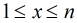
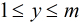
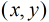
        为满足且和的的对数

       为满足且和的的对数

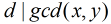
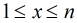
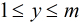
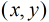
 那么，一个数对x,y要满足它们的gcd是i的倍数，则x和y中都必须包含i这个因子，所以F(i)=⌊N/i⌋·⌊M/i⌋。所以反演后得到

所以得到 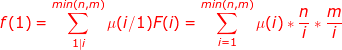 ，因为要去重，所以后面再减去(1,b)区间的(x,y)对数的一半；

#include<iostream>
#include<string.h>
#define ll long long
using namespace std;
ll mu[100007],prime[100007];
bool mark[100007];
void getmu()
{
        mu[1]=1;
        ll cnt=0;
        for(ll i=2;i<100007;i++){
                if(!mark[i]){
                        prime[cnt++]=(ll)i;
                        mu[i]=-1;
                }
                for(ll j=0;j<cnt&&i*prime[j]<100007;j++){
                        mark[i*prime[j]]=1;
                        if(i%prime[j]){
                                mu[i*prime[j]]=-mu[i];
                        }else{
                                mu[i*prime[j]]=0;
                                break;
                        }
                }
        }
}
int main()
{
        int T;
        ll a,b,c,d,k,ans1,ans2;
        getmu();
        scanf("%d",&T);
        for(int ca=1;ca<=T;ca++){
                scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
                printf("Case %d: ",ca);
                if(!k){printf("0
");continue;}
                b/=k,d/=k;
                if(b>d) swap(b,d);
                ans1=ans2=0;
                for(ll i=1;i<=b;i++)
                        ans1+=mu[i]*(b/i)*(d/i);
                for(ll i=1;i<=b;i++)
                        ans2+=mu[i]*(b/i)*(b/i);
                printf("%lld
",ans1-ans2/2);
        }
        return 0;
}