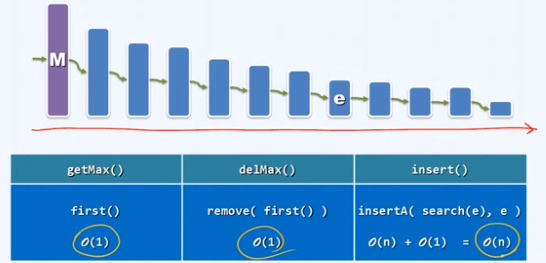
一、需求与动机
元素接受访问的次序按照优先级,而非FIFO
场景
夜间门诊
病情危急的优先治疗
多任务调度
每个任务都有一个指标,指标都是动态变化的,操作系统总是挑选指标最大的任务交由CPU处理
应用、算法与特点
问题模式:
接口规范

纯虚函数
a2基本实现
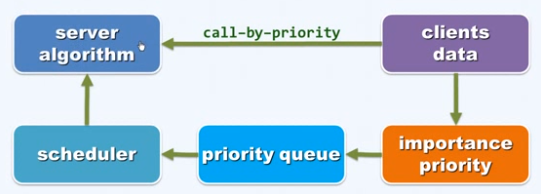
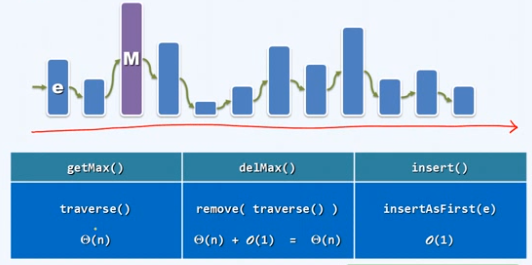
基于向量
有序向量
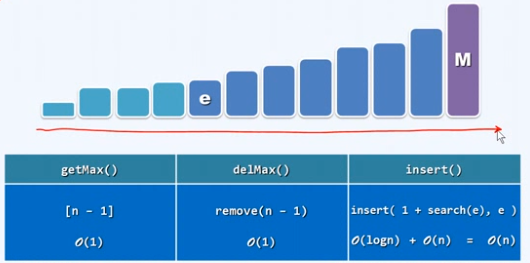
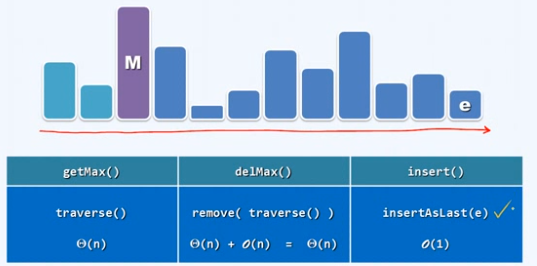
基于列表
有序列表
BBST
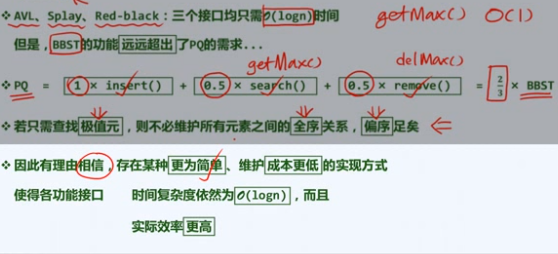
b1完全二叉堆:结构
在向量和树之间找一个折中的结构
完全二叉树
Complete Binary Tree
平衡因子处处非负的AVL
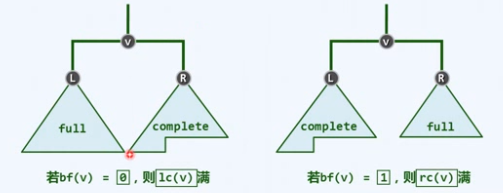
结构性
逻辑上,等同于完全二叉树
物理上,直接借助向量实现

逻辑节点与物理元素,依层次遍历次序彼此应对

对于向量中任意秩为i的元素,如果父节点存在,其秩为i-1再除以2,比如秩为11和12的元素,父节点存在,编号为5
如果秩为i的元素,有左孩子,左孩子的秩是两倍的i再加1,比如,对于6而言,左孩子为13
如果秩为i的元素,有右孩子,右孩子的秩是(i+1)*2,比如6的右孩子为14
利用C++的多重继承

堆序性
数值上,只要0<i,必满足![]()
即任何一个节点在数值上不会超过父亲
上面的图是秩,不是值
最大元只可能是根节点

b2完全二叉堆:插入与上滤
算法
为插入词条e,只需将e作为末元素接入向量
//结构性自然保持
//若堆序性也未破坏,则完成


否则 //只能是e与其父节点违反堆序性
e与其父节点换位 //若堆序性因此恢复,则完成
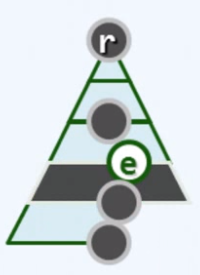
否则 //依然只能是e与其(新的)父节点违反堆序性
e再与其父节点换位

不断重复...直到
e与其父亲满足堆序性,或者e到达堆顶点(没有父亲)
这一过程,就是所谓的上滤(percolate up)
实例
这里所标注的数值都是元素的优先级而非其所对应的秩
由5个词条构成的完全二叉堆,上面的完全二叉树是逻辑结构,下面是物理上对应的向量结构,物理上的向量首元素是逻辑上完全二叉树的根节点,根据约定是数据集中的最大值

插入为5的词条
作为末元素插入到向量中,在逻辑上等效于在完全二叉树的底层向右侧拓展了一个节点,这种拓展没有破坏完全二叉堆的结构性,新引入的词条和父亲违背堆序性,二者互换位置。物理上是在向量中进行的

交换后
仍与上层的父亲违反堆序性
继续交互位置
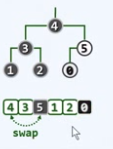
交换后

实现

效率
b3完全二叉堆:删除
最大元素始终在堆顶,故为删除之,只需
摘除向量首元素,代之以末元素e


//结构性保持;若堆序性依然保持则完成
否则 //即e与孩子们违背堆序性
e与孩子中的大者互换

//若堆序性因此恢复,则完成
否则 //即e与其(新的)孩子们...
e再次与孩子中的大者换位

下滤
实例
删除最大元5

1移动到根,左右孩子都必它大,局部违反了堆序性,其他地方保持堆序性
找到相对更大的4,互换位置,下滤
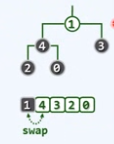
交换后,依然每符合堆序性,1和2互换

交换后

实现

b4完全二叉堆:批量建堆
自上而下的上滤

效率
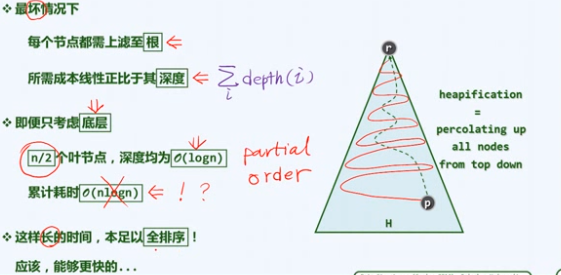
自下而上的下滤

实例
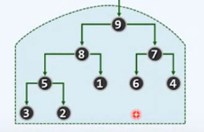
由9个节点构成的完全二叉树
在物理上的向量图,最末尾内部节点所对应的秩应该为9/2下整减1,即3,下面节点上的3是值,纯属巧合
初始情况下每个叶节点都可以认为自成为一个子堆,画紫圈的部分形成了典型的模式,一个局部子树根,以及左右两个子堆,任务是左右子堆合并
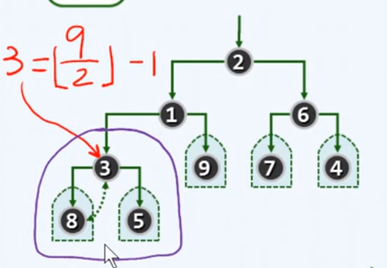
对局部子树根节点3进行下滤
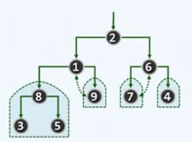
接下来往前一个的内部节点,6,对局部子树根6进行下滤; 接下来轮到内部节点1,对1下滤

对根节点做下滤,完成最终的合并
效率

c堆排序
选取

就地
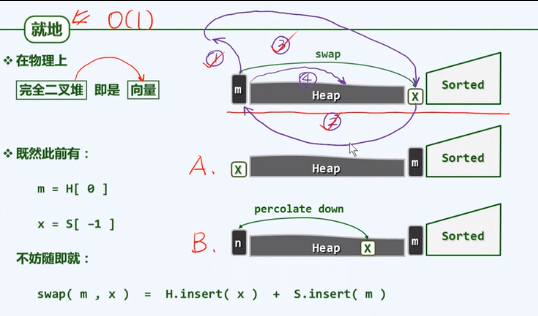
实现

实例:建堆
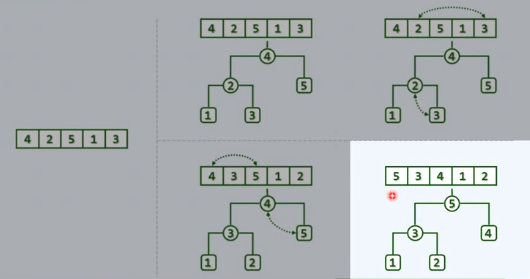
几次下滤后,最终得到了完全二叉堆
选取+调整
开始整个向量都是未排序的部分,已排序的部分为空
令堆顶与末元素互换位置
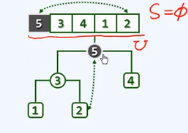
互换后,已排序序列有第一个元素5,黑色; 新的堆顶做下滤调整

剩下的四个元素依然恢复为一个堆,尽管规模减1个单位;最大元素4成为新的堆顶
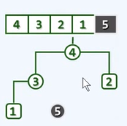
将堆顶与末元素1互换
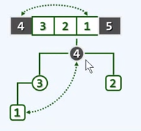
将堆顶摘出,归入到已排序序列中;下滤调整,保证是合法的堆


堆顶3与末元素2互换,堆顶摘出,归入到有序序列中
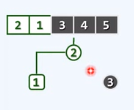
重复步骤
xa1左式堆:结构
引入左式堆,为了完成堆合并
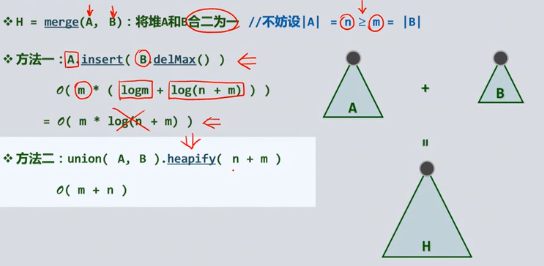
堆合并
单侧倾斜
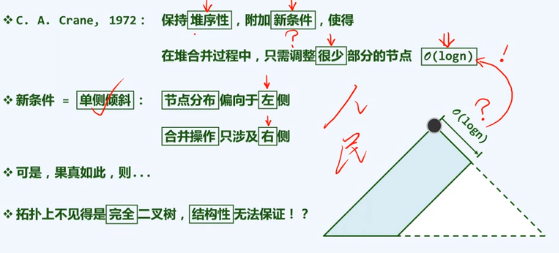
空节点路径长度

左倾性&左式堆
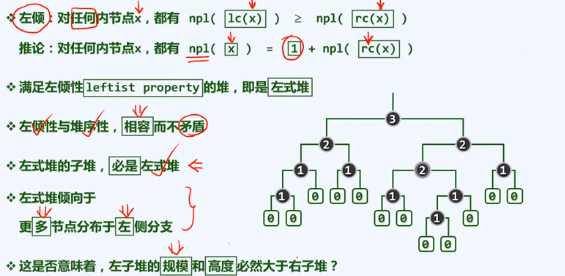
右侧链
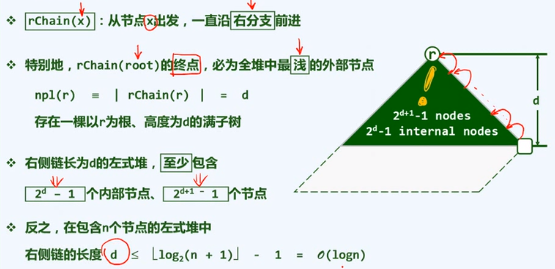
xa2左式堆:合并
LeftHeap
不满足结构结构性,物理结构不再保持紧凑型,不使用向量,使用树
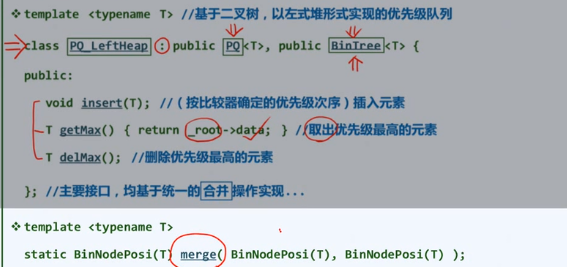
算法


实例
两个堆合并
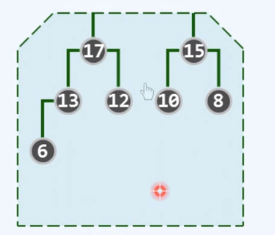
前者树根大于后者树根,无需互换,17为a,15为b,a的右孩子12
转为右子堆与b堆的合并问题

比较两个子堆的根节点,15大于12,互换名称,前者记作b,后者记作a

a、b堆合并; a的右子树是8
转化为子堆8和子堆12合并

两者应互换名称
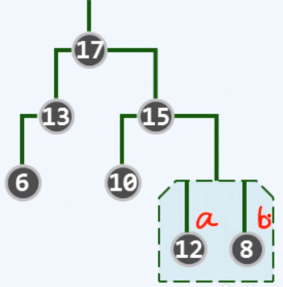
a右孩子为空,在接下来的递归层次上,直接返回节点8,并将8作为节点12的右孩子
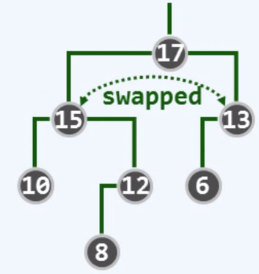
左倾,左右子堆互换位置

递归返回到节点15
15左右NPL都为1,左倾性没有破坏,逆行而上,到17,左孩子NPL为1,右为2
经过一次对换,交换17节点的左右孩子
xa3左式堆:插入与删除
insert()

delMax()
