树状数组详解

一、引入和概念

平常我们会遇到一些对数组进行维护查询的操作，比较常见的，修改某点的值、求某个区间的和。

数据规模不大的时候，对于修改某点的值是非常容易的，复杂度是O(1)，但是对于求一个区间的和就要扫一遍了，复杂度是O(N)。

如果实时的对数组进行M次修改或求和，最坏的情况下复杂度是O(M*N)，当规模增大后这是划不来的。

而树状数组干同样的事复杂度却是O(M*lgN)。

树状数组是一个查询和修改复杂度都为log(n)的数据结构。

主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。

看完概念后发现和线段树的功能类似，实际上树状数组和线段树确实类似，不过也有不同，具体区别和联系如下：

1.两者在复杂度上同级, 但是树状数组的常数明显优于线段树, 其编程复杂度也远小于线段树.

2.树状数组的作用被线段树完全涵盖, 凡是可以使用树状数组解决的问题, 使用线段树一定可以解决, 但是线段树能够解决的问题树状数组未必能够解决.

3.树状数组的突出特点是其编程的极端简洁性, 使用lowbit技术可以在很短的几步操作中完成树状数组的核心操作，与之相关的便是其代码效率远高于线段树。

二、实现

树状数组，重点是在树状的数组

一颗普通的二叉树如下

叶子结点代表A数组A[1]~A[8]

现在变形一下

 现在定义每一列的顶端结点C[]数组 ，如下图

 

 

 

C[i]代表 子树的叶子结点的权值之和// 这里以求和举例

如图可以知道

C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

 

其中C数组的求法如下：

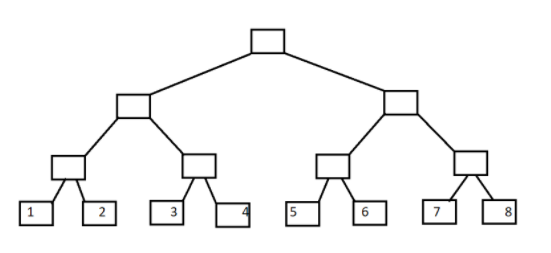
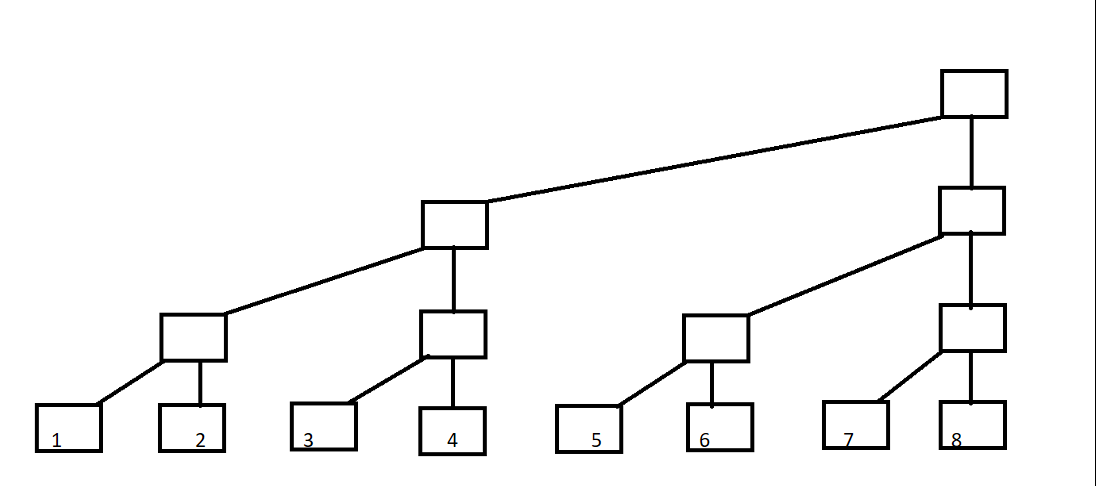
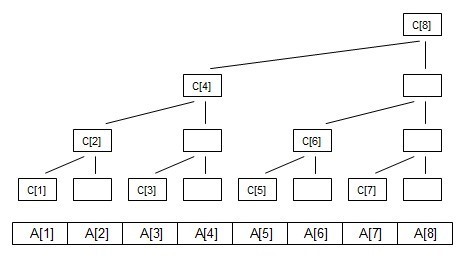
C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; （k为i的二进制中从最低位到高位连续零的长度）例如i=8时，k=3;

 

为了更好的理解上面的公式，将1-32的2^k计算出来如下：

 

有了这个表格之后对照上面的式子就可以轻松的知道每一个C代表的哪几个数的和。比如

C[8]，由上图知2^k为8，那么

C[24]，由上图知2^k为8，那么

 

 

这是我们通过简单的计算得出来的值，那么应该如何转换成编程语言呢，大神们给出了非常巧妙的方法，利用下面的函数可以求出2^k的值。

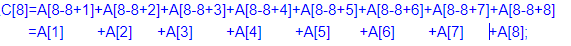
int lowbit(int x)
{
    return x&-x;
}

 为什么这样可以呢？这里复制了一篇证明可以看一下。

首先明白一个概念，计算机中-i=（i的取反+1），也就是i的补码 
而lowbit，就是求（树状数组中）一个数二进制的1的最低位，例如01100110，lowbit=00000010；再例如01100000，lowbit=00100000。 
所以若一个数（先考虑四位）的二进制为abcd，那么其取反为(1-a)(1-b)(1-c)(1-d)，那么其补码为(1-a)(1-b)(1-c)(2-d)。 
如果d为1，什么事都没有-_-|||但我们知道如果d为0，天理不容2Σ( ° △ °|||)︴ 
于是就要进位。如果c也为0，那么1-b又要加1，然后又有可能是1-a……直到碰见一个为补码为0的bit，我们假设这个bit的位置为x 
这个时候可以发现：是不是x之前的bit的补码都与其自身不同？，x之后的补码与其自身一样都是0？ 
例如01101000，反码为10010111，补码为10011000，可以看到在原来数正数第五位前，补码的进位因第五位使其不会受到影响，于是0&1=0,； 
但在这个原来数“1”后，所有零的补码都会因加1而进位，导致在这个“1”后所有数都变成0，再加上0&0=0，所以他们运算结果也都是零； 
只有在这个数处，0+1=1，连锁反应停止，所以这个数就被确定啦O(∩_∩)O 

 有了上面的基础，我们就可以解决很多问题了。重要的操作有两个，分别是更新和求和。

1.更新操作

void update(int k,int x)
{
    for(int i=k;i<=n;i+=lowbit(i))
        C[i]+=x;
}

2.求和操作

int getsum(int x)
{
    int ans=0;
    for(int i=x;i;i-=lowbit(i))//i要大于0
        ans+=C[i];
    return ans;
}

 

三、代码

#include <iostream>
#include <cstdlib>
#include <algorithm>
#include <string>
#include <cstring>
#include <stdio.h>
#include <queue>
#define IO ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
using namespace std;
#define N 50100
int n;
int c[N];
int lowbit(int x)
{
    return x&(-x);
}
void update(int k,int x)
{
    for(int i=k; i<=n; i+=lowbit(i))
        c[i]+=x;
}
int getsum(int x)
{
    int ans=0;
    for(int i=x; i; i-=lowbit(i)) //i要大于0
        ans+=c[i];
    return ans;
}
int main()
{
    IO;
    int T;
    cin>>T;
    int logo=1;
    while(T--)
    {
        memset(c,0,sizeof(c));
        cin>>n;
        for(int i=1; i<=n; i++)
        {
            int t;
            cin>>t;
            update(i,t);
        }
        char s[100];
        cout<<"Case "<<logo++<<":"<<endl;
        while(1)
        {
            cin>>s;
            if(s[0]=='E')
                break;
            if(s[0]=='Q')
            {
                int a,b;
                cin>>a>>b;
                cout<<getsum(b)-getsum(a-1)<<endl;
            }
            if(s[0] == 'S')
            {
                int a,b;
                cin>>a>>b;
                update(a,-b);
            }
            if(s[0] == 'A')
            {
                int a,b;
                cin>>a>>b;
                update(a,b);
            }
        }
    }
    return 0;
}